Alien Dictionary

Question

892 · Alien Dictionary - LintCode

There is a new alien language which uses the latin alphabet. However, the order among letters are unknown to you. You receive a list of non-empty words from the dictionary, where words are sorted lexicographically by the rules of this new language. Derive the order of letters in this language

1. You may assume all letters are in lowercase.
2. The dictionary is invalid, if string a is prefix of string b and b is appear before a.
3. If the order is invalid, return an empty string.
4. There may be multiple valid order of letters, return the smallest in normal lexicographical order.
5. The letters in one string are of the same rank by default and are sorted in Human dictionary order.

Example 1:

Input：["wrt","wrf","er","ett","rftt"]
Output："wertf"

Explanation：
from "wrt" and "wrf" ,we can get 't'<'f'
from "wrt" and "er" ,we can get 'w'<'e'
from "er" and "ett" ,we can get 'r'<'t'
from "ett" and "rftt" ,we can get 'e'<'r'

So return "wertf"

Example 2:

Input：["z","x"]
Output："zx"
Explanation：
from "z" and "x"，we can get 'z' < 'x'
So return "zx"

Solution

Intuition

Given the input

["wrt","wrf","er","ett","rftt"]

If we can some how build the relationship, for example:

t -> f
w -> e
r -> t
e -> r

We can then have the following map:

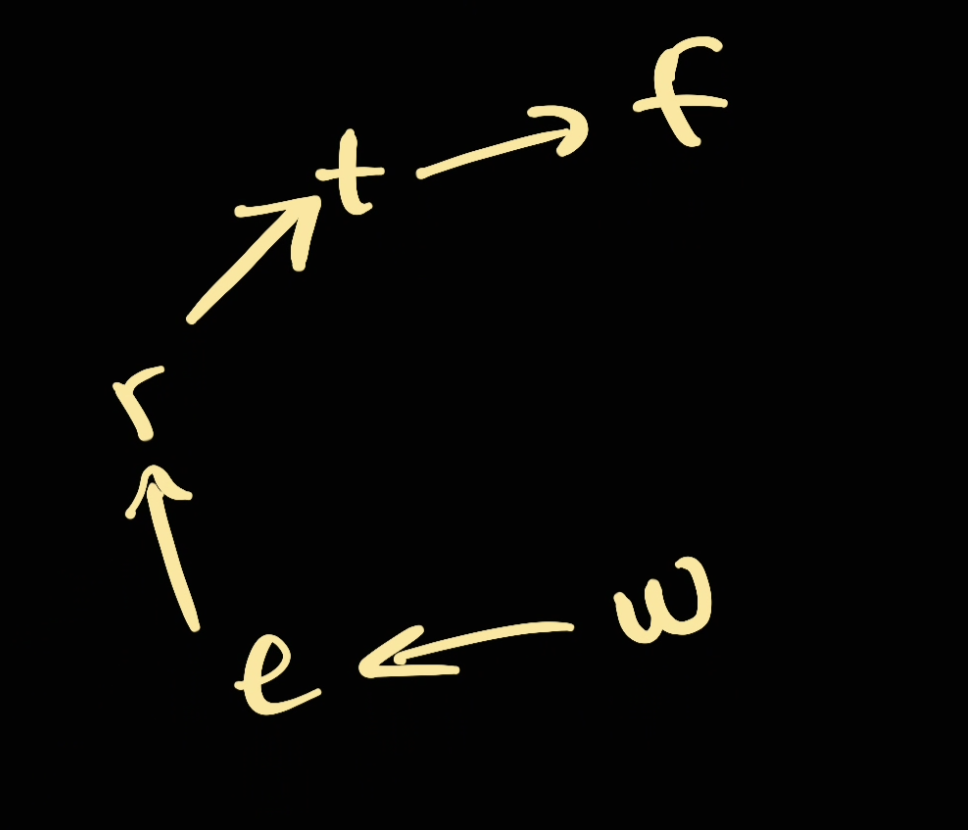
As a result, it becomes the Topological Sort (Kahn's algorithm) problem where we can start from the node that has 0 indegree (w) and keep adding character by character.

However, what if we have something like [ab, adc], what would be the result?

We would then have this following map:

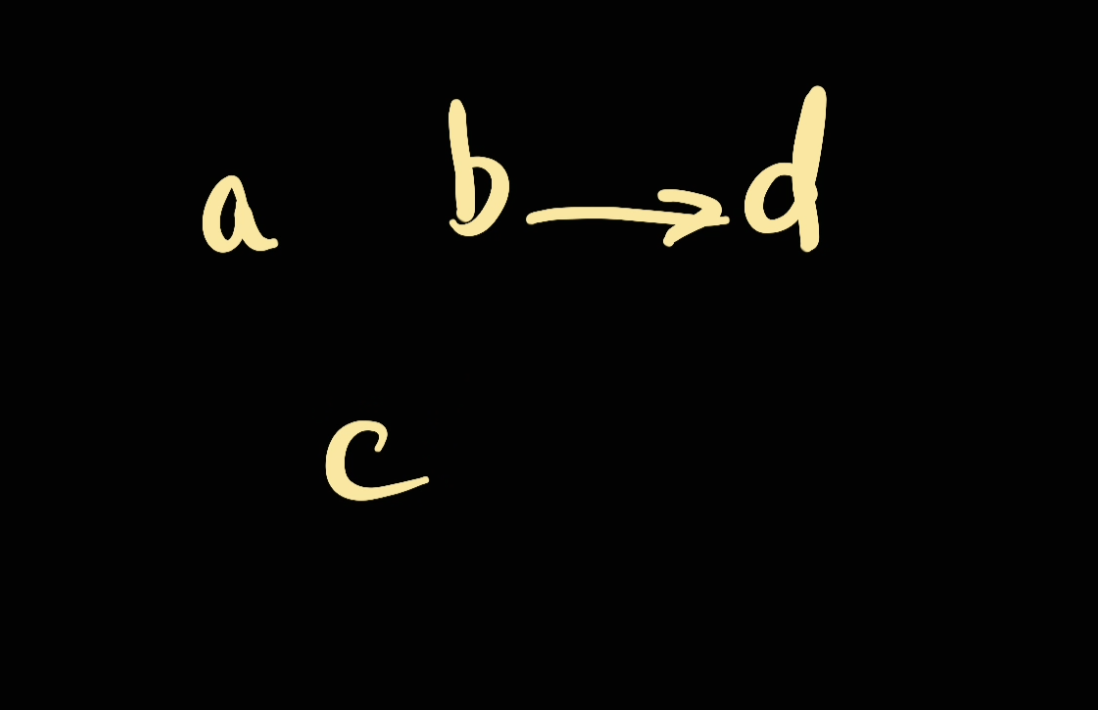
However, since the requirement is to return in human lexicographical order, we will need to go [a, b, c ,d].

As a result, normal topoligical sort is not enough, we need to visit the node in sorted order as well.

In this case, we can modify the [[Topological Sort (Kahn's algorithm)#^7b2308|topological sort of using a queue for toVist]] to use a Heap Theory instead. It's beacause when doing heappop() given a heapified (created in heap order) array, it should pop in alphabetical order.

We should be able to add character in order. If the string contains all the characters in the words, we should return the string. Else we should return empty string ("") to indicate that we cannot complete the topological sort traversal, hence the dictionary is not valid.

Iterate through pair

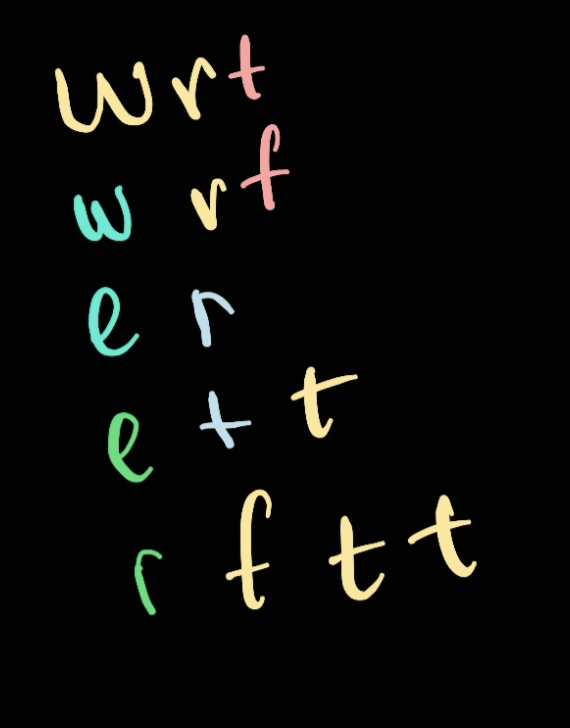
We can start by comparing the following pairs of characters:

• t -> f
• w -> e
• r -> t
• e -> r

As a results, we can compare these in pair:

• If the first pair of characters are the same, we move on to the next pair of character
• Once we find a different character, we start mapping the relationship of the 2 characters.

For example:

Given these 2 words: `wrt` and `wrf`

wrt
wrf
^
Here, w == w, we compare the next character

wrt
wrf
 ^
Here, r == r, we compare the next character


wrt
wrf
  ^
Here, t != f, we map the relationship of these 2 characters:
t -> f

We can then repeat this with every pair: (wrt and wrf), (wrf and er), (er and et), (et and rf)

Mapping the relationship

To map the relationship, we can use the concept of Adjacency List.

Implementation

from heapq import heapify, heappop, heappush
from typing import *
from collections import defaultdict

class App:
    def alienOrder(self, words: List[str]) -> str:
        adjacencyList = defaultdict(lambda: [])
        indegreeEdges = { c: 0 for word in words for c in word }

        for i in range(len(words) - 1):
            if self.isInvalidDictionaryCheck(words[i], words[i + 1]):
                return ""
            
            for j in range(min(len(words[i]), len(words[i + 1]))):
                currCharacter = words[i][j]
                nextCharacter = words[i + 1][j]
                
                if currCharacter != nextCharacter:
                    adjacencyList[currCharacter].append(nextCharacter)
                    indegreeEdges[nextCharacter] += 1
                    break

        toVisit = [c for c in indegreeEdges if indegreeEdges[c] == 0]
		# We use the heap here to pop in alphabetical order
		# as of the question's requirement
        heapify(toVisit)
        result = []
        
        while toVisit:
            currCharacter = heappop(toVisit)
            result.append(currCharacter)
            
            for nextCharacter in adjacencyList[currCharacter]:
                indegreeEdges[nextCharacter] -= 1
                
                if indegreeEdges[nextCharacter] == 0:
                    heappush(toVisit, nextCharacter)
        
        if len(indegreeEdges) != len(result):
            # Cannot visit all characters
            return ""
        
        return "".join(result)

    def isInvalidDictionaryCheck(self, firstWord, secondWord):
	    # Base on condition `2.` of the requirement 
        return secondWord in firstWord and len(firstWord) > len(secondWord)

Time complexity: $O((|V| + |E|)\times log(n))$

• $V$ is the number of unique character
• $E$ is the number of edges (connection between each character)
• log(n) because we perform heap operation (heappopj) for each $V$ and heappush for each $E$

Space complexity: $O(|V| + |E|)$ because we need to keep track of indegreeEdges and adjacencyList