Topological Sort (Kahn'S Algorithm)

Definition

Ways to identify

• When you have to do A first before we do B. And then we do C or elements that dependent to each other.

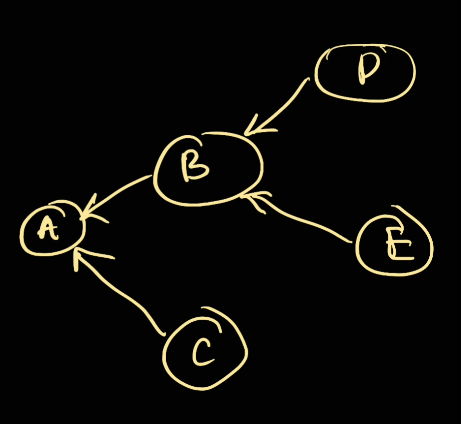
For example, in this case:

• A depends on B and C
• B depends on D and E

Note: for topological sort to works, the graph needs to be Directed Acyclic Graph

We can represent this graph as following:

if __name__ == "__main__":
    vertices = ["A", "B", "C", "D", "E"]
    dependencies = [
        ["B", "D"],  # B dependent on D
        ["B", "E"],  # B dependent on E
        ["A", "B"],  # A dependent on B
        ["A", "C"],  # A dependent on C
    ]
    print(topological(vertices, dependencies))

Then the algorithm is as following:

1. Build an Adjacency List from the child to the parent using hashmap
   • This is to navigate to the parent once we finished visiting the child
2. Build a inDegree map to keep track which parent still have dependencies
   • The ones without dependencies will be add to our queue for visiting

Note: in here we're going to use a queue for toVisit vertices. The reason why we use a queue is because we want to visit in BFS order. If using a stack, we go half DFS half BFS it doesn't make sense (because the nature of stack is exploring the top node) ^7b2308

Implementation

def topological(vertices: List[str], dependencies: List[List[int]]) -> List[int]:
    dependencyMap = {
        vertex: [] for vertex in vertices
    }

    # Since the dependencyMap is the map from child to parent
    # We need this to keep track of the number of dependency the parent has
    inDegree = {
        vertex: 0 for vertex in vertices
    }

    # Build the road map from child node to parent
    for parent, child in dependencies:
        dependencyMap.get(child).append(parent)
        inDegree[parent] += 1

    # Add the non dependent vertices in a queue to start
    # We set this as a queue for consistent order of BFS (if a stack it will be half-ass DFS/BFS due to stack's nature)
    toVisit = deque(
        [vertex for vertex in vertices if inDegree.get(vertex) == 0]
    )

    visited = []

    # Topological sort algorithm
    while toVisit:
        curr = toVisit.pop()
        visited.append(curr)

        for parent in dependencyMap[curr]:
            inDegree[parent] -= 1
            if inDegree.get(parent) == 0:
                toVisit.appendleft(parent)

    return visited

Time Complexity: $O(V + E)$

• $V$: the number of vertex
• $E$: the number of dependencies (edges)

Space complexity: $O(V + E)$

• Because we have the map of each vertex and then the dependency map as well

Some example:

• https://leetcode.com/problems/course-schedule/description/