Rotting Oranges

Question

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

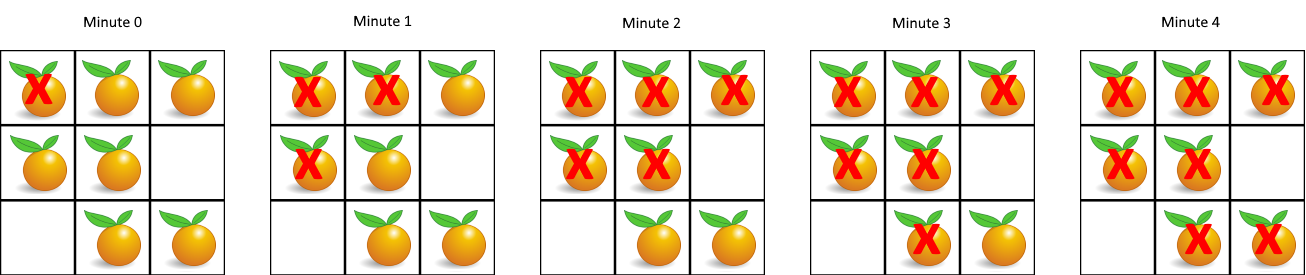
Examples

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Solution

This is a very basic Graph Traversal > BFS Traversal problem where we start with 1 cell and we expand to other cell.

In the case for BFS, we want to explore this graph iteratively.

Because we want to count the minute every time we go up, we can consider doing something like Tree BFS (Level-by-level)

So the algorithm will go as follow:

1. Loop through every oranges to find the starting point (the rotten one)
2. Perform BFS at that point, add everything to a queue to keep track
3. For each level we go through, we increment the minutes counter by 1
4. We return minutes if we can explore all the oranges, otherwise -1

Implementation

class App:
    def __init__(self) -> None:
        self.ROTTEN = 2
        self.NORMAL = 1
        self.EMPTY = 0

    def orangesRotting(self, grid):
        if not grid or len(grid) == 0: raise Exception("Illegal arugments")
        self.grid = grid
        
        minutes = 0
        rottenOrangesPositionQueue = deque() #  
        normalOrangesCount = self.countNormalOrangesAndPopulateRottenQueue(rottenOrangesPositionQueue) # 6
        originalRottenOrangesLength = len(rottenOrangesPositionQueue)
        rottenOrangesCount = 0 # 6
        firstRun = True
        
        while rottenOrangesPositionQueue:
            for _ in range(len(rottenOrangesPositionQueue)): # 1
                currentRottenOrange = rottenOrangesPositionQueue.popleft() #1, 0
                row, col = currentRottenOrange
                grid[row][col] = self.ROTTEN
                rottenOrangesCount += 1
                
                for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                    nextRow, nextCol = row + dr, col + dc
                    
                    if self.isValidOrange(nextRow, nextCol) and (nextRow, nextCol) not in rottenOrangesPositionQueue:
                        rottenOrangesPositionQueue.append((nextRow, nextCol))
            
            if not firstRun: 
                minutes += 1
            else: 
                firstRun = False
        
        return minutes if normalOrangesCount == rottenOrangesCount - originalRottenOrangesLength else - 1

[!note]

In here we don't count the minutes for the first run, this is the requirement from the question — because we added all the rotten to the array first to explore.

So for example if we have

[
	[0, 1, 0]
	[1, 2, 1]
	[0, 1, 0]
]

The amount of minutes to rotten all these oranges is 1. If we count the first run (since we're starting from (1,1)) it will be 2. Therefore we need to skip the first run.

Time complexity: $O(mn + mn) = O(mn)$

• We have $m \times n$ to loop through the graph once to find all the rotten one.
• We have another $m \times n$ for BFS

Space complexity: $O(mn)$ for the number of element in the queue.

Optimisation

In here, we can clean the code a bit. If you look in here, we don't really need to calculate the rottenOrangesCount just for the sake of calculating

if normalOrangesCount == rottenOrangesCount - originalRottenOrangesLength

We can just simply use the normalOrangesCount and minus it until it get 0

So everytime there is a rotten orange, we can substract the normal orange count.

Which we can change it to as follow:

    def orangesRotting(self, grid):
        if not grid or len(grid) == 0: raise Exception("Illegal arugments")
        self.grid = grid
        
        minutes = 0
        rottenOrangesPositionQueue = deque() #  
        normalOrangesCount = self.countNormalOrangesAndPopulateRottenQueue(rottenOrangesPositionQueue) # 6
        firstRun = True
        
        while rottenOrangesPositionQueue:
            for _ in range(len(rottenOrangesPositionQueue)): # 1
                currentRottenOrange = rottenOrangesPositionQueue.popleft() #1, 0
                row, col = currentRottenOrange
                grid[row][col] = self.ROTTEN
                
                if not firstRun: normalOrangesCount -= 1 # Note here
                
                for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                    nextRow, nextCol = row + dr, col + dc
                    
                    if self.isValidOrange(nextRow, nextCol) and (nextRow, nextCol) not in rottenOrangesPositionQueue:
                        rottenOrangesPositionQueue.append((nextRow, nextCol))
            
            if not firstRun: 
                minutes += 1
            else: 
                firstRun = False

		# Note here
        return minutes if normalOrangesCount == 0 else - 1

Next, in here we need to determine if it's firstRun or not. Because initally we've added the already exists rottenOranges as well. So we need to make up for it.

As a result, it might be better if we can just calculate the result at the children level.

Which means we will substract the orange count when we add new oranges into the queue instead of actually traverse into one

This means at the start we will not count the already existing rotten oranges but only the children of it.

However, we will need another if condition to only do the loop if there are oranges left to visit. This is because if we don't do like this, it will actually go into the last level of the queue to visit the last nodes and thus increasing the 1 minute.

Since the last level is the end already and we counted late (to skip the parents), we can just stop trying to explore at the last level.

Therefore we have this final code:

class App:
    def __init__(self) -> None:
        self.ROTTEN = 2
        self.NORMAL = 1
        self.EMPTY = 0

    def orangesRotting(self, grid):
        if not grid or len(grid) == 0: raise Exception("Illegal arugments")
        self.grid = grid
        
        minutes = 0
        rottenOrangesPositionQueue = deque() 
        normalOrangesCount = self.countNormalOrangesAndPopulateRottenQueue(rottenOrangesPositionQueue) # 6
        
        while rottenOrangesPositionQueue and normalOrangesCount > 0:
            for _ in range(len(rottenOrangesPositionQueue)): # 1
                currentRottenOrange = rottenOrangesPositionQueue.popleft() #1, 0
                row, col = currentRottenOrange
                grid[row][col] = self.ROTTEN
                
                
                for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
                    nextRow, nextCol = row + dr, col + dc
                    
                    if self.isValidOrange(nextRow, nextCol) and (nextRow, nextCol) not in rottenOrangesPositionQueue:
                        rottenOrangesPositionQueue.append((nextRow, nextCol))
                        normalOrangesCount -= 1
            
            minutes += 1
        
        return minutes if normalOrangesCount == 0 else - 1
    
    def countNormalOrangesAndPopulateRottenQueue(self, queue: Deque):
        normalOrangesCount = 0
        for row in range(len(self.grid)):
            for col in range(len(self.grid[0])):
                orange = self.grid[row][col]
                if (orange == self.NORMAL):
                    normalOrangesCount += 1
                elif (orange == self.ROTTEN):
                    queue.append((row, col))
        return normalOrangesCount
    
    def isValidOrange(self, row, col):
        withinBoundary = not (row < 0 or col < 0 or row >= len(self.grid) or col >= len(self.grid[0]))
        return withinBoundary and self.grid[row][col] == self.NORMAL