Graph Traversal

Given a graph in a format of an 2D array, we want to traverse this graph.

For example

graph = [
	[5, 4, 7,10],
	[1, 3, 2, 0],
	[9, 4,11, 1]
]

DFS traversal

[!note]
For DFS we need to have a visited set to keep track of the node that we have already gone through.

Without visited set, it will keep looping in circle

Guard check at DFS

We can do a DFS traversal with the border check in the next loop.

Doing this will has an advantage that even if we call the wrong function at the start (for example we call self.dfs(-1, -1)), the program will exit itself.

class App:
    graph: List[List[int]]
    
    def traverse(self, graph: List[List[int]]):
        self.graph = graph
        self.dfs(0, 0)
        pass
    
    def dfs(self, row, col, visited: Set[Tuple[int, int]] = set()): 
        if row < 0 or col < 0 or row >= len(self.graph) or col >= len(self.graph[0]):
            return
        
        if (row, col) in visited: return
        
        visited.add((row, col))
        
        self.visit(row, col)
        
        for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
            nextRow, nextCol = row + dr, col + dc
            self.dfs(nextRow, nextCol)

    def visit(self, row, col):
        print("Visited: ", row, col)

The traversal will go as follows:

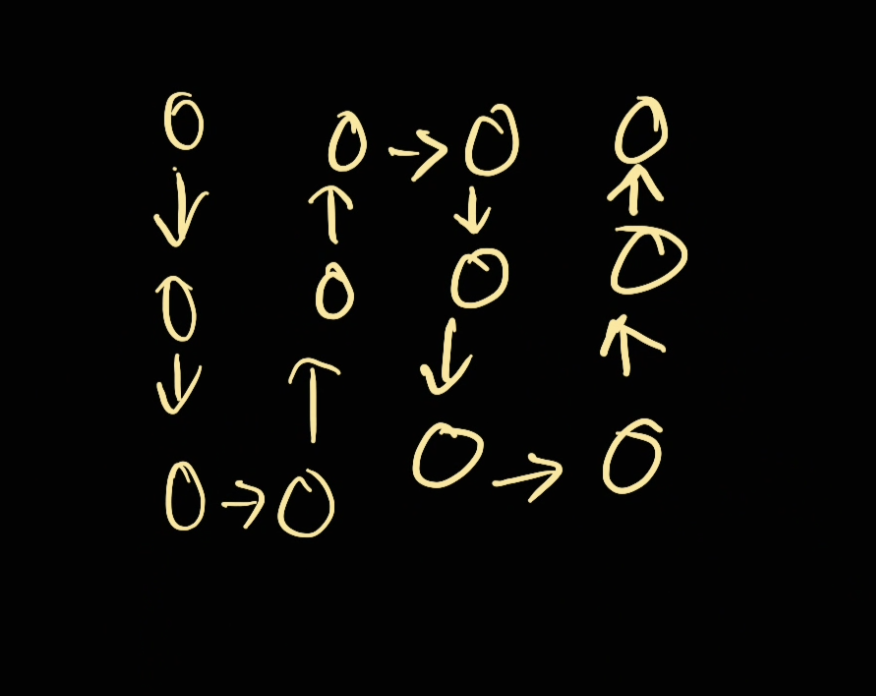
Guard check before DFS

Sometimes if we want we can guard check before we go in the function:

def dfs(self, row, col, visited: Set[Tuple[int, int]] = set()): 
	if (row, col) in visited: return
	
	visited.add((row, col))
	
	self.visit(row, col)
	
	for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
		nextRow, nextCol = row + dr, col + dc

		if self.isWithinBoundary(nextRow, nextCol):
			self.dfs(nextRow, nextCol)
			
def isWithinBoundary(self, row, col):
	return not (row < 0 or col < 0 or row >= len(self.graph) or col >= len(self.graph[0]))

When is it useful

This becomes handy when you when you need some information of the current row before going to the next row.

For example: If we can only go if the nextNumber <= currentNumber, this becomes handy.

Let's revisit our graph:

graph = [
	[5, 4, 7,10],
	[1, 3, 2, 0],
	[9, 4,11, 1]
]

We can then just change our if statement to below:

def dfs(self, row, col, visited: Set[Tuple[int, int]] = set()): 
	if (row, col) in visited: return
	
	visited.add((row, col))
	
	self.visit(row, col)

	for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)]: 
		nextRow, nextCol = row + dr, col + dc

		# Change here only
		if self.isWithinBoundary(nextRow, nextCol) and self.graph[row][col] >= self.graph[nextRow][nextCol]:            
			self.dfs(nextRow, nextCol)

This will output visit as follow sequence:

Visited:  0 0
Visited:  1 0
Visited:  0 1
Visited:  1 1
Visited:  1 2
Visited:  1 3

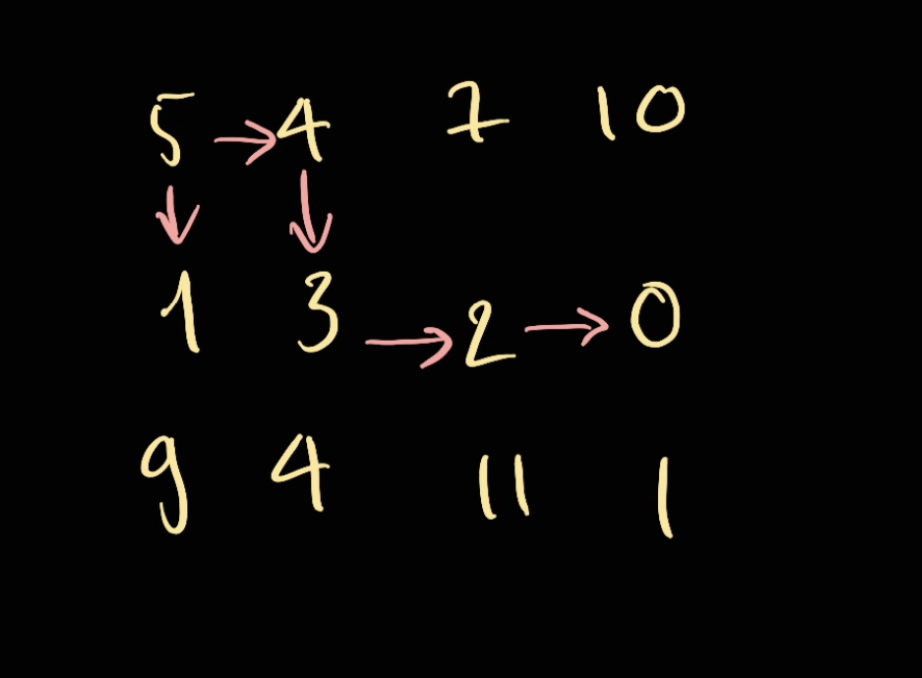
Same scenario but if we do guard check at DFS

We can also do the same thing for Guard check at DFS but however we need to modify our function such that now dfs will take in the previous weight to compare and increase the complexity of the code:

def dfs(self, row, col, previousWeight = float('-inf'), visited: Set[Tuple[int, int]] = set()): 
	if not self.isWithinBoundary(row, col) or (previousWeight != float('-inf') and self.graph[row][col] > previousWeight): return
	if (row, col) in visited: return
	
	visited.add((row, col))
	
	self.visit(row, col)
	
	for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
		nextRow, nextCol = row + dr, col + dc
		self.dfs(nextRow, nextCol, previousWeight = self.graph[row][col])

This will also produce:

Visited:  0 0
Visited:  1 0
Visited:  0 1
Visited:  1 1
Visited:  1 2
Visited:  1 3

However if you look at here, we need to:

1. Assign a default previousWeight = float('-inf') in this case
2. Update the previousWeight in the next function to be the currentWeight
3. Compare if:
   1. The previousWeight is not default (float(-inf))
      • The reason why is we need to validate if the currentWeight <= previousWeight to go. However, this wouldn't work if we set default previousWeight to -inf. Since there is nothing smaller than -inf.
      • Doing this will bypass the first iteration to make sure our loop still run
   2. So when it's not -inf — which means for the next iteration (not the first one), we can then confirm if currentWeight <= previousWeight or not. If currentWeight > previousWeight, we shouldn't perform DFS here.

BFS Traversal

For BFS traversal, we need to use Deque as a queue.

Common mistakes

def bfs(self, row, col):
	queue = deque()
	visited = set()

	queue.append((row, col))
	
	while queue:
		row, col = queue.popleft()
		
		visited.add((row, col)) # NOTE HERE
		self.visit(row, col)
		
		for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
			nextRow, nextCol = row + dr, col + dc
			
			if self.isWithinBoundary(nextRow, nextCol) and (nextRow, nextCol) not in visited:
				queue.append((nextRow, nextCol))

In here, we should not add to the visited set during the current node. Why? — because we should consider visited when we're adding the node in we should not wait until we actually visiting that node to add that in.

For example in this case, we added a node in visited set before we're adding our candidates to our queue. Therefore the (nextRow, nextCol) not in visited is not valid anymore.

Thus, we need to add in (nextRow, nextCol) not in queue as well to guard this condition — However, this is very expensive since deque is linkedlist, this computation will cost $O(n)$

Since we're visiting whatever we're adding to our queue anyways, we need to make sure we're adding it to visited set when we're adding it in the queue.

What to do

def bfs(self, row, col):
	queue = deque()
	visited = set()

	queue.append((row, col))
	visited.add((row, col)) # NOTE HERE
	
	while queue:
		row, col = queue.popleft()
		self.visit(row, col)
		
		for (dr, dc) in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
			nextRow, nextCol = row + dr, col + dc
			
			if self.isWithinBoundary(nextRow, nextCol) and (nextRow, nextCol) not in visited:
				visited.add((nextRow, nextCol))
				queue.append((nextRow, nextCol)) # NOTE HERE

Note: That we put node in visited as soon as we add them to the queue since we're going to visit them anyways in the next loop.

This will guarantee that we don't visit one node twice and therefore keeping our time complexity is $O(V + E)$

As a result, this will go as the following:

Visited:  0 0
Visited:  1 0
Visited:  0 1
Visited:  2 0
Visited:  1 1
Visited:  0 2
Visited:  2 1
Visited:  1 2
Visited:  0 3
Visited:  2 2
Visited:  1 3
Visited:  2 3

With graph:

graph = [
	[5, 4, 7,10],
	[1, 3, 2, 0],
	[9, 4,11, 1]
]