Pacific Atlantic Water Flow

Question

There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.

The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).

The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.

Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.

Example 1:

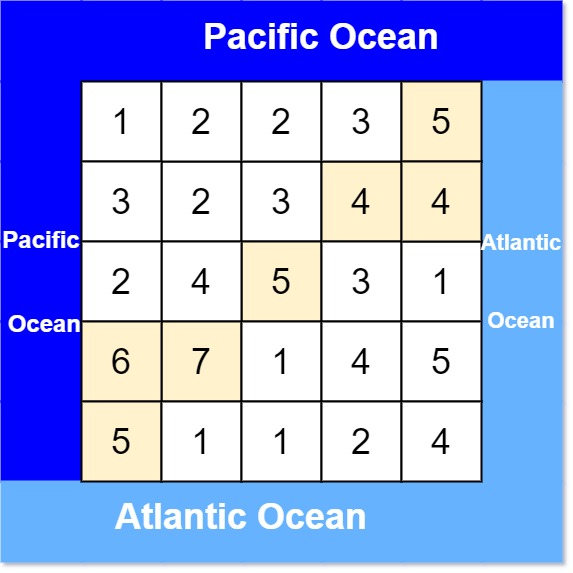
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0,4]: [0,4] -> Pacific Ocean 
       [0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean 
       [1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean 
       [1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean 
       [2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean 
       [3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean 
       [3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean 
       [4,0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.

Example 2

Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.

Solution

Brute force solution

One of the obvious way is to bruteforce through our answer. In here, it's intuitive to think of a solution to traverse from a cell to see if it reaches the ocean or not.

For example, given the example above, we can try to start with node 1 and see how far we can go:

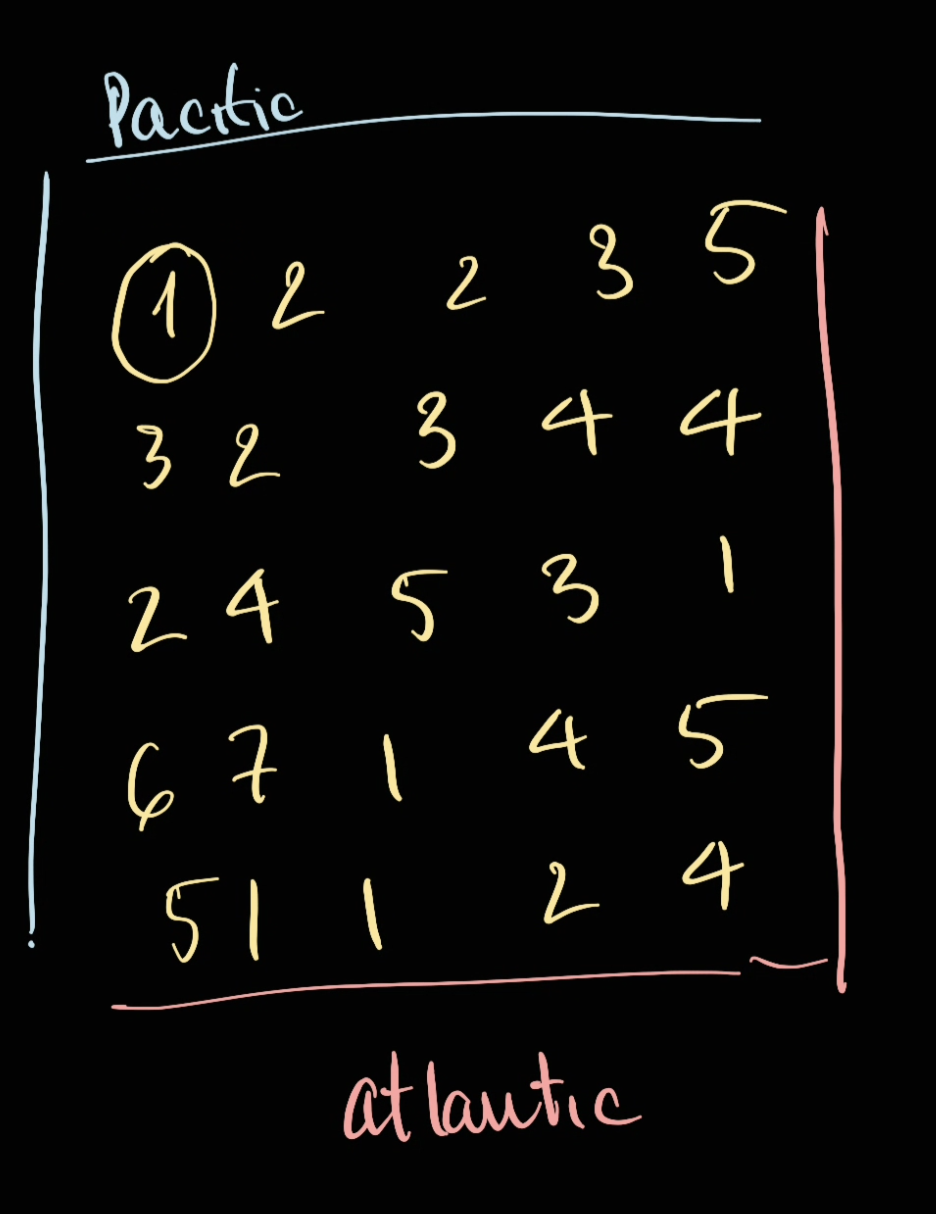
In here we can see that 1 cannot go anywhere, therefore, we're going to node 2:

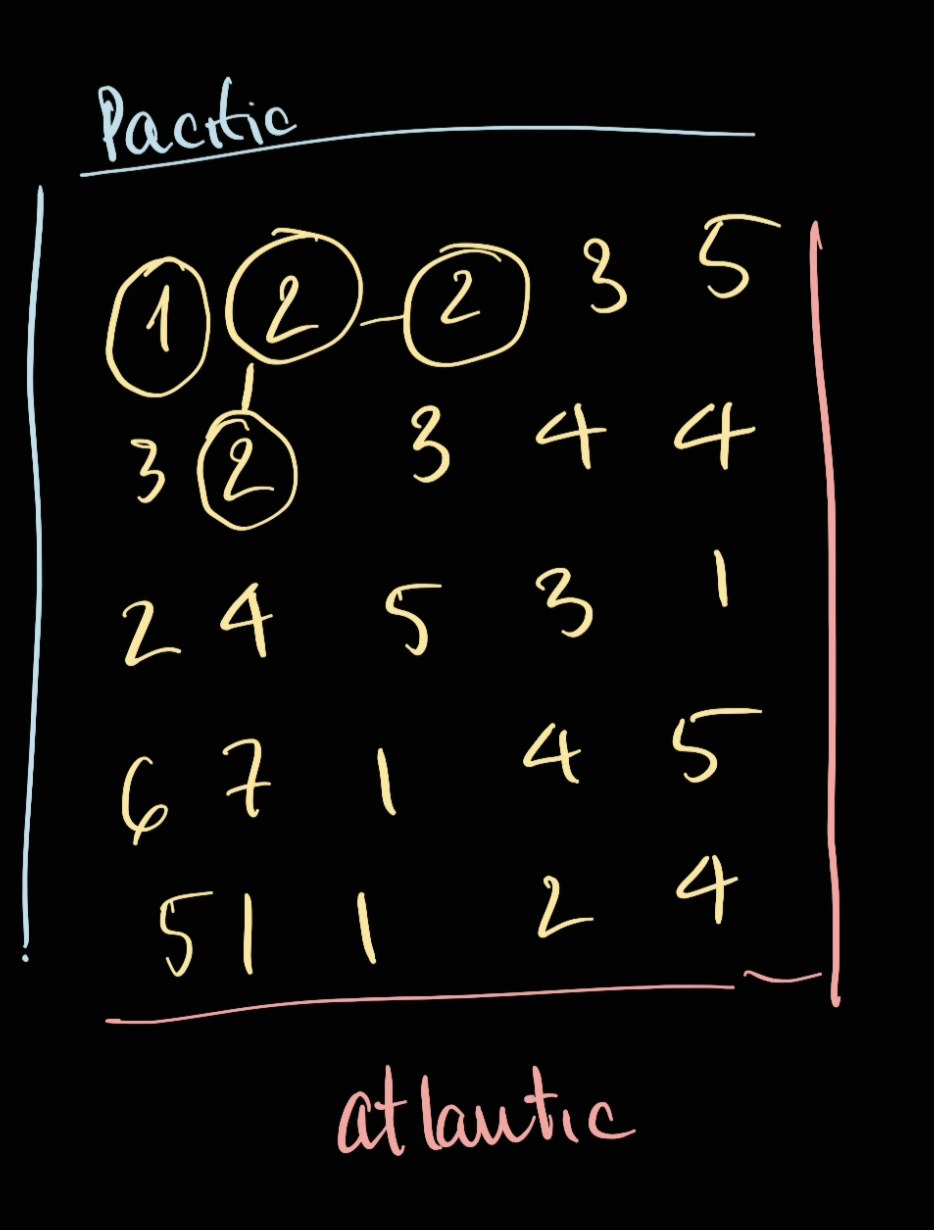
As you can see, from 2 we can expand out but not much, as a result we can only reach to Pacific but not Atlantic.

We will repeat this process for every node inside the ocean.

Implementation

We can do a DFS for each cell in the ocean. Note that for each DFS traversal we have:

• visited set:
  • For the DFS function to work, because it needs to travel from one node to another node without overlapping the path
• ocean set

  • We need to keep track of successful records into this ocean set in order to find which node in both ocean set later.

  • However this needs to be distinct from the visited set because a node inside visited set might not be inside ocean set.

    Therefore we cannot use the ocean set itself as BFS traversal visited set as is not large enough to cover all our search space.

[!note]
In here we chose DFS because if we choose BFS, we need to pop out the cells from the ocean. And because of that, we would not have the cell in each ocean to perform a compare

class App:
    def __init__(self) -> None:
        self.ATLANTIC = 1
        self.PACIFIC = 0
        pass

    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        if not heights or len(heights) == 0: 
            raise Exception("Illegal Arugment")
        
        result = []
        
        canFlowAtlantic = set()
        canFlowPacific = set()
        
        for row in range(len(heights)):
            for col in range(len(heights[0])):
                
                if self.canReachOcean(heights, row, col, canFlowAtlantic, oceanType = self.ATLANTIC, visited=set()):
                    canFlowAtlantic.add((row, col))
                
                if self.canReachOcean(heights, row, col, canFlowPacific, oceanType = self.PACIFIC, visited=set()):
                    canFlowPacific.add((row, col))

                if ((row, col) in canFlowPacific and (row, col) in canFlowAtlantic):
                    result.append([row, col])

        return result
    
    def hasReachedOcean(self, heights, oceanType, row, col):
        if oceanType == self.ATLANTIC: 
            return row == len(heights) - 1 or col == len(heights[0]) - 1

        if oceanType == self.PACIFIC: 
            return row == 0 or col == 0
        
        raise Exception("Invalid oceantype", oceanType)
    
    def isInvalid(self, heights, row, col):
        return row < 0 or col < 0 or row >= len(heights) or col >= len(heights[0])
    
    def canReachOcean(self, heights, row, col, canFlowToOcean: Set[Tuple[int, int]], oceanType, visited: Set[Tuple[int, int]]) -> bool:

        if (row, col) in visited: return False
        if (row, col) in canFlowToOcean: return True

        visited.add((row, col))
        
        if self.hasReachedOcean(heights, oceanType, row, col): 
            return True
        
        for dr, dc in [(1,0), (-1, 0), (0, 1), (0, -1)]:
            nextRow, nextCol = row + dr, col + dc
            
            if not self.isInvalid(heights, nextRow, nextCol) and heights[nextRow][nextCol] <= heights[row][col]:
                if (self.canReachOcean(heights, nextRow, nextCol, canFlowToOcean, oceanType, visited=visited)):
                    canFlowToOcean.add((nextRow, nextCol))
                    return True

        return False

For each cells, we do a DFS to check if the cell can reach to the ocean or not. If it can we will put that into the corresponding ocean set.

Time complexity: $O(m \times n \times (m \times n)) = O((mn)^2)$

• For each row, column we need to traverse $m \times n$ because of the DFS
• We need to repeat the above step for every row, columnar

Space complexity: $O(m \times n \times 2 (m + n) + 2 (m + n) + (m + n))$

• We have an array of $m \times n$ as given. For each cell:
  • We have a visited set of $m + n$ pairs of (row, col) for each DFS
  • We also have 2 visited set for each ocean
• We also have additional 2 $m + n$ ocean set outside of pair (row, col)
• Lastly we have a result set of $m + n$ (row, col)

Optimised solution

If you think about this problem, it's better to to traverse backward from the solution. Because ideally we want to find the cells that can reach to the ocean, so can search from the ocean to see which are the cells that can reach the ocean

In here since we're traversing from the answer space, we only need:

• ocean set:
  • This could be using as a visited set as well as the ocean set.
  • Since we're traversing from the answer space, we only add candidates that is reachable to the solution in our search space. Therefore our $searchSpace \equiv answerSpace$

Implementation

class App:
    graph: List[List[int]]
    
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        if not heights or len(heights) == 0: 
            raise Exception("Illegal Arugment")

        self.graph = heights
        
        pacificReachable: Set[Tuple[int, int]] = set()
        atlanticReachable: Set[Tuple[int, int]] = set()
        
        # Explore out from Pacific
        for c in range(len(self.graph[0])):
            self.dfsExplore(0, c, pacificReachable)
        
        for r in range(len(self.graph)):
            self.dfsExplore(r, 0, pacificReachable)

        # Explore out from Atlantic
        for c in range(len(self.graph[0])):
            self.dfsExplore(len(self.graph) - 1, c, atlanticReachable)
        
        for r in range(len(self.graph)):
            self.dfsExplore(r, len(self.graph[0]) - 1, atlanticReachable)
        
        result = []
        # Collect the tiles that reaches both pacific and atlantic
        for row in range(len(self.graph)):
            for col in range(len(self.graph[0])):
                tile = (row, col)
                
                if tile in pacificReachable and tile in atlanticReachable:
                    result.append([row, col])
                    
        return result

    def dfsExplore(self, row, col, reachableOcean: Set[Tuple[int, int]]):
        if (row, col) in reachableOcean: return
        
        reachableOcean.add((row, col))
        
        for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
            nextRow, nextCol = row + dr, col + dc
            
            if not self.isWithinBoundary(nextRow, nextCol) or self.graph[row][col] > self.graph[nextRow][nextCol]:
                continue
            
            self.dfsExplore(nextRow, nextCol, reachableOcean)
    
    def isWithinBoundary(self, row, col):
        return not (row < 0 or col < 0 or row >= len(self.graph) or col >= len(self.graph[0]))

Time complexity: $O(4(m \times n))$

• A cell can be visited 4 times at most from 4 sides of the ocean. And we have $m \times n$ cells in total.
  Space complexity: $O(3(m + n))$
• We only have 2 ocean set of pair (row, col) — therefore $m + n$
• Our DFS reuse the ocean set instead of having its own visited set
• We have another result array of (row, col) worst case $m \times n$

Optimisation

We can simply combine the two identical for c and for r together to make it shorter, for example:

class App:
    graph: List[List[int]]
    
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        if not heights or len(heights) == 0: 
            raise Exception("Illegal Arugment")

        self.graph = heights
        
        pacificReachable: Set[Tuple[int, int]] = set()
        atlanticReachable: Set[Tuple[int, int]] = set()
        
        for c in range(len(self.graph[0])):
            self.dfsExplore(0, c, pacificReachable)
            self.dfsExplore(len(self.graph) - 1, c, atlanticReachable)
        
        for r in range(len(self.graph)):
            self.dfsExplore(r, 0, pacificReachable)
            self.dfsExplore(r, len(self.graph[0]) - 1, atlanticReachable)

        result = []
        # Collect the tiles that reaches both pacific and atlantic
        for row in range(len(self.graph)):
            for col in range(len(self.graph[0])):
                tile = (row, col)
                
                if tile in pacificReachable and tile in atlanticReachable:
                    result.append([row, col])
                    
        return result

    def dfsExplore(self, row, col, reachableOcean: Set[Tuple[int, int]]):
        if (row, col) in reachableOcean: return
        
        reachableOcean.add((row, col))
        
        for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
            nextRow, nextCol = row + dr, col + dc
            
            if not self.isWithinBoundary(nextRow, nextCol) or self.graph[row][col] > self.graph[nextRow][nextCol]:
                continue
            
            self.dfsExplore(nextRow, nextCol, reachableOcean)
    
    def isWithinBoundary(self, row, col):
        return not (row < 0 or col < 0 or row >= len(self.graph) or col >= len(self.graph[0]))

BFS Solution

The Problem can also be done as BFS and it will be a bit faster as well

class App:
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        atlanticCells = set()
        pacificCells = set()
        
        for i in range(0, len(heights)):
            self.discoverCells((i, len(heights[0]) - 1), atlanticCells, heights)
            self.discoverCells((i, 0), pacificCells, heights)

        for i in range(0, len(heights[0])):
            self.discoverCells((0, i), pacificCells, heights)
            self.discoverCells((len(heights) - 1, i), atlanticCells, heights)
        
        result = []

        for cell in pacificCells:
            if cell in atlanticCells: 
                row, col = cell
                result.append([row, col])
        
        return result


    def discoverCells(self, position: Tuple[int, int], ocean: Set[Tuple[int, int]], heights: List[List[int]]) -> None:
        queue = deque([position])
        ocean.add(currPosition)

        while queue:
            currPosition = queue.popleft()
            row, col = currPosition

            for dr, dc in [(1, 0), (0, 1), (-1, 0), (0, -1)]:
                newPosition = row + dr, col + dc
                
                if self.isValid(newPosition, currPosition, heights) and newPosition not in ocean:
                    ocean.add(newPosition)
                    queue.append(newPosition)
        
    
    def isValid(self, newPosition: Tuple[int, int], prevPosition: Tuple[int, int], heights: List[List[int]]) -> bool: 
        nRow, nCol = newPosition
        row, col = prevPosition

        if (nRow < 0 or nCol < 0 or nRow >= len(heights) or nCol >= len(heights[0])):
            return False

        return heights[nRow][nCol] >= heights[row][col]