Union Find
Definition
Union find is an algorithm to deal with the concept of connected graph to find the root of a connected component. That's particularly useful to solve Number Of Connected Component in a graph problem.
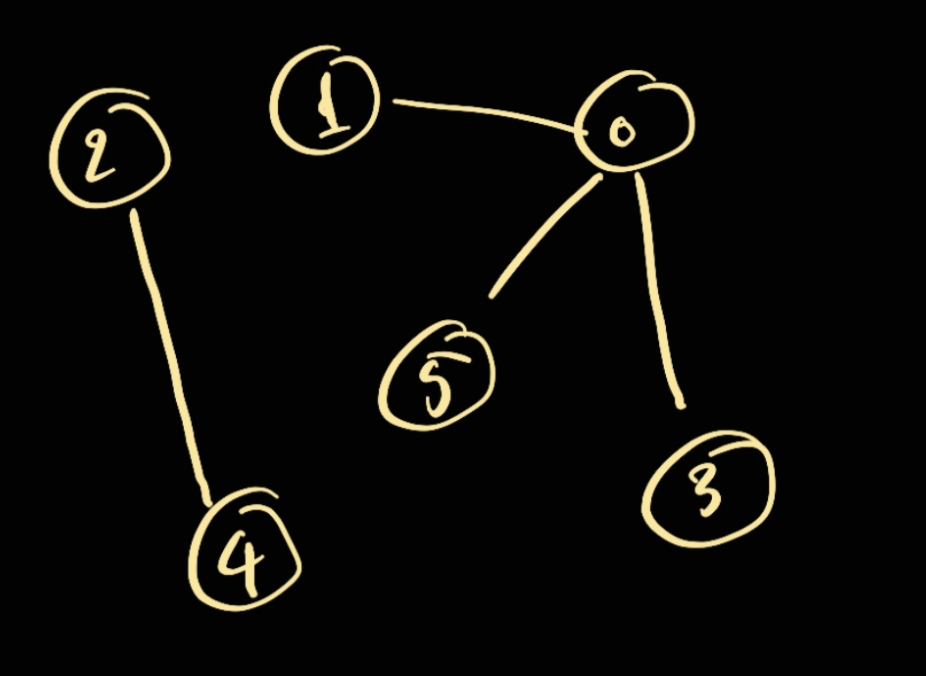
For example if we have the following graph.
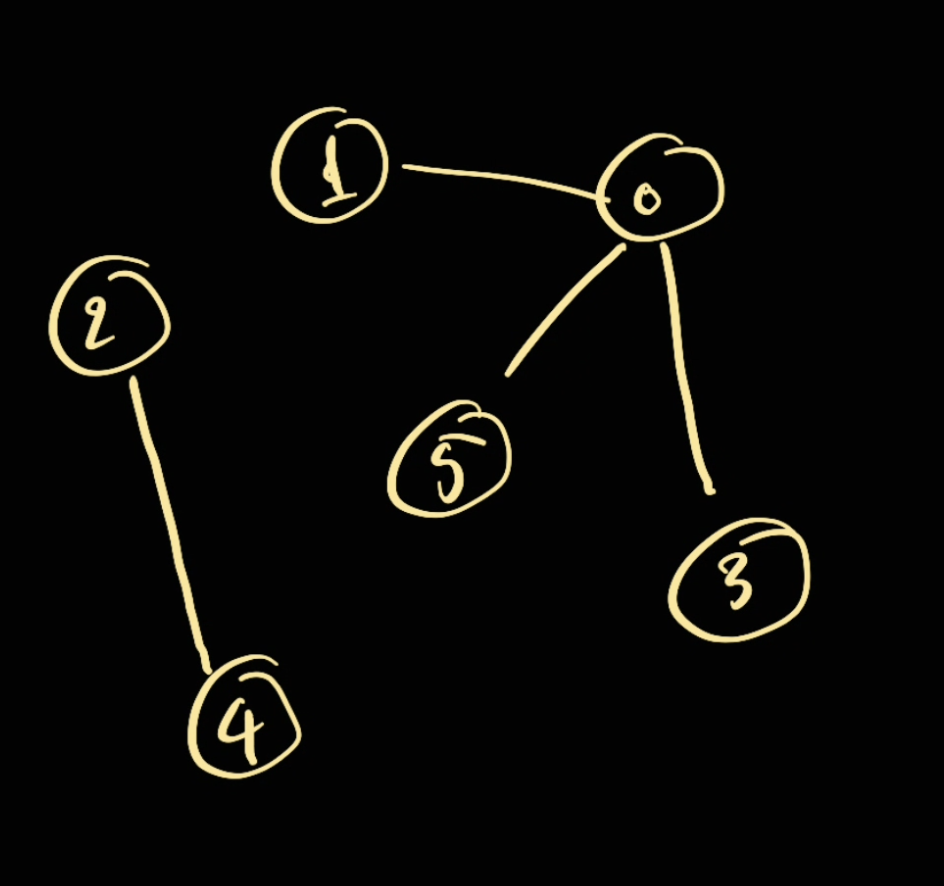
The following operation hold true:
find(5) -> 0: since0is the root of5union(2, 5),find(2) -> 0since we combine group2with group5which leads to the following new graph: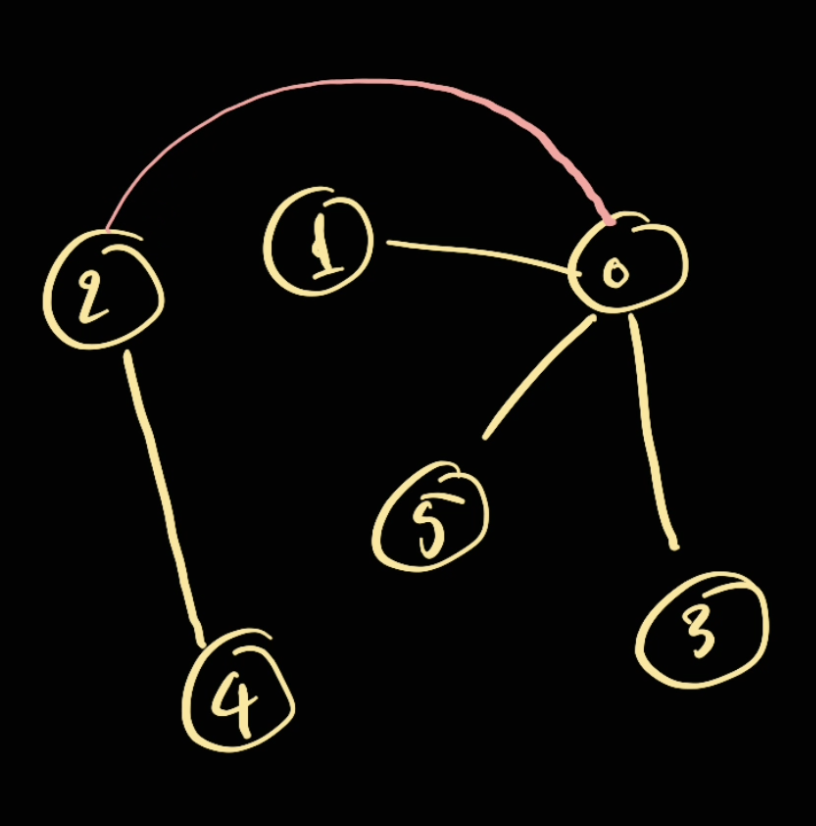
Basic Algorithm
The algorithm requires 2 datastructures:
parents: List[int]— list to contain the parents.- For example the above graph can be represented as
[0, 0, 0, 0, 2, 0]:- parent of everything is
0 - parent of
4is2
- parent of everything is
- Initially given a non-connected graph, a node will be the parent of itself. So
[0,1,2,3,4,5]for this one: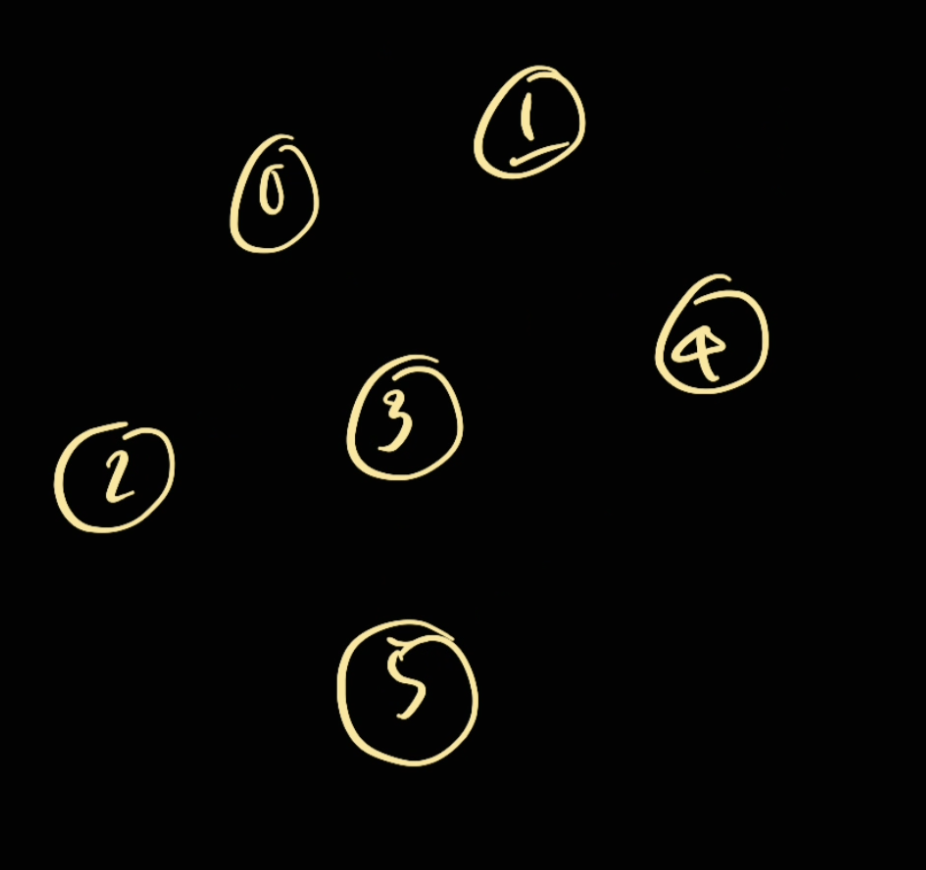
- For example the above graph can be represented as
size (ranking): List[int]— the size of the current group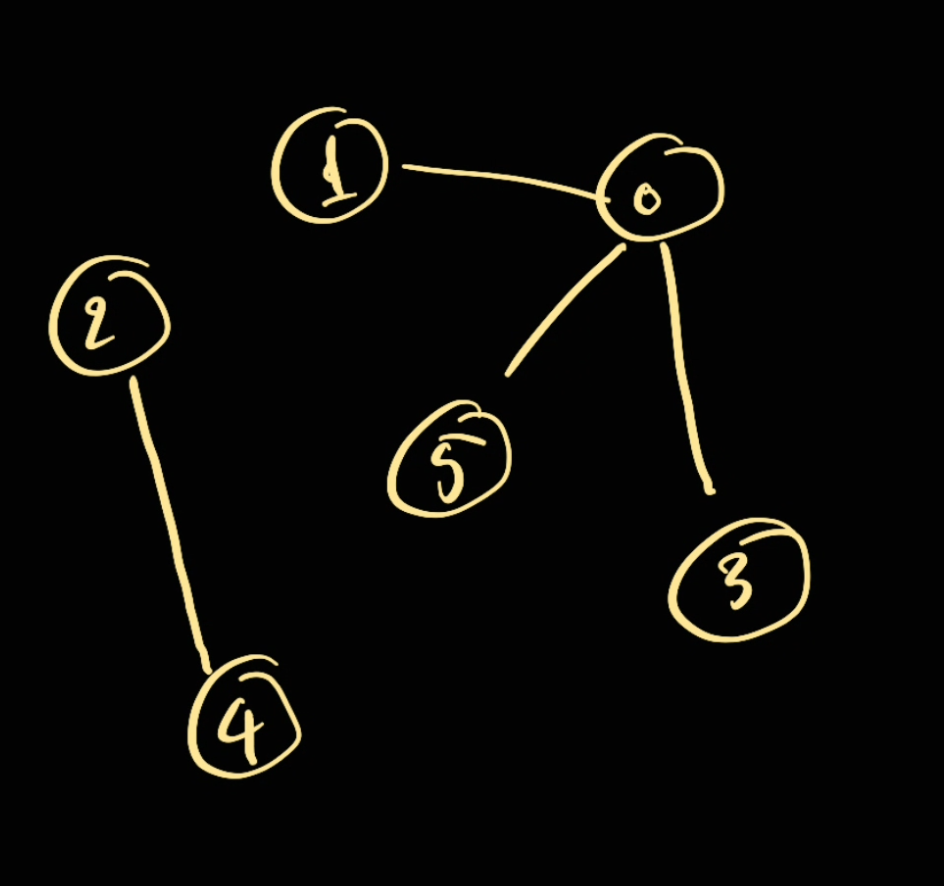
- In this case should be
[4,0,2,0,0,0]0has 4 elements2has 2 elements- the rest has
0elements
- In this case should be
Union
To union 2 groups, we simply union the parents of the 2 group together.
So for example, given the following case:
If we're doing a union(4, 3), we are essentially merging the root parent of 4 (2) with the parent of 3 (0)
Now we have 2 choices, either we merge 2 into 0 or 0 into 2:
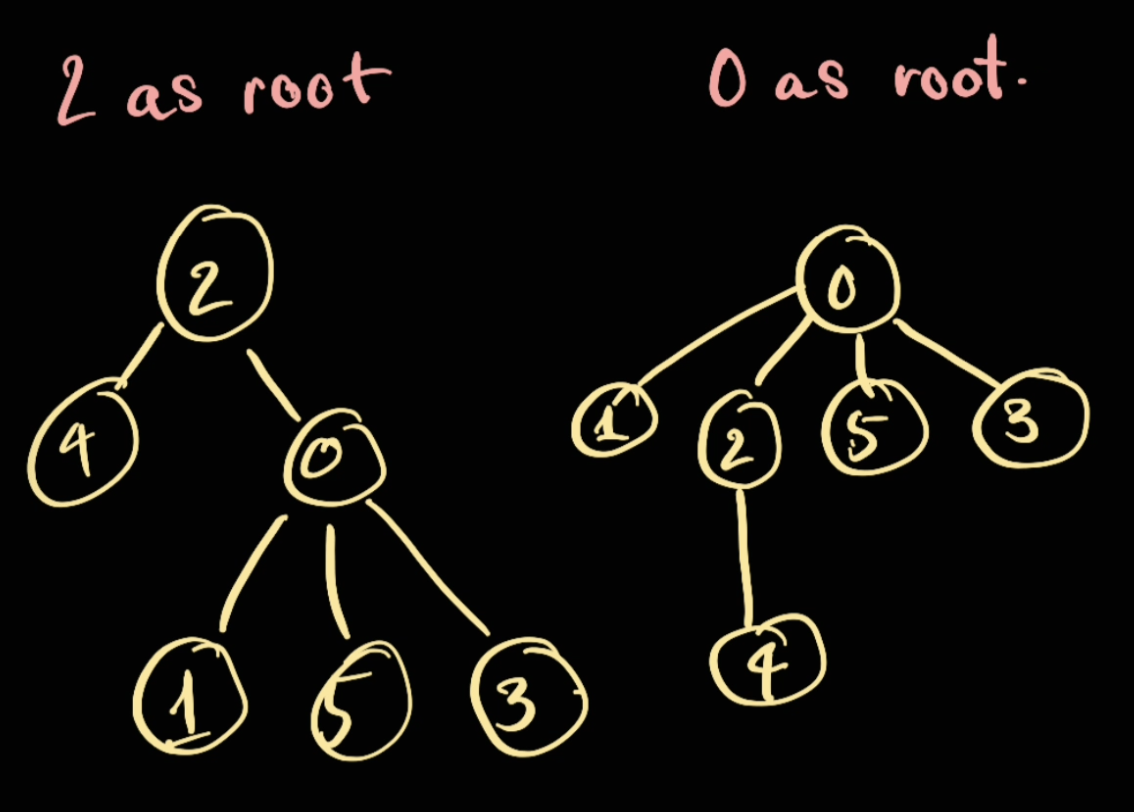
Both ways of merging should work, however, as a rule of thumbs, we should merge the smaller group into the larger group to reduce the size of the tree.
[!important]
This is the reason why we keep track of thesizearray
Implementation
class UnionFind:
def __init__(self, n) -> None:
self.parents = [i for i in range(0, n)]
self.componentSize = [1] * n
def union(self, a: int, b: int) -> bool:
rootA = self.find(a)
rootB = self.find(b)
# If they have the same root, nothing needs to be done
if rootA == rootB:
return False
if self.componentSize[rootA] < self.componentSize[rootB]:
self.parents[rootA] = self.parents[rootB]
self.componentSize[rootB] += self.componentSize[rootA]
self.componentSize[rootA] = 0
else:
self.parents[rootB] = self.parents[rootA]
self.componentSize[rootA] += self.componentSize[rootB]
self.componentSize[rootB] = 0
return True
Time complexity:
- for assigning the parent
Find
The find method will find the root of a node.
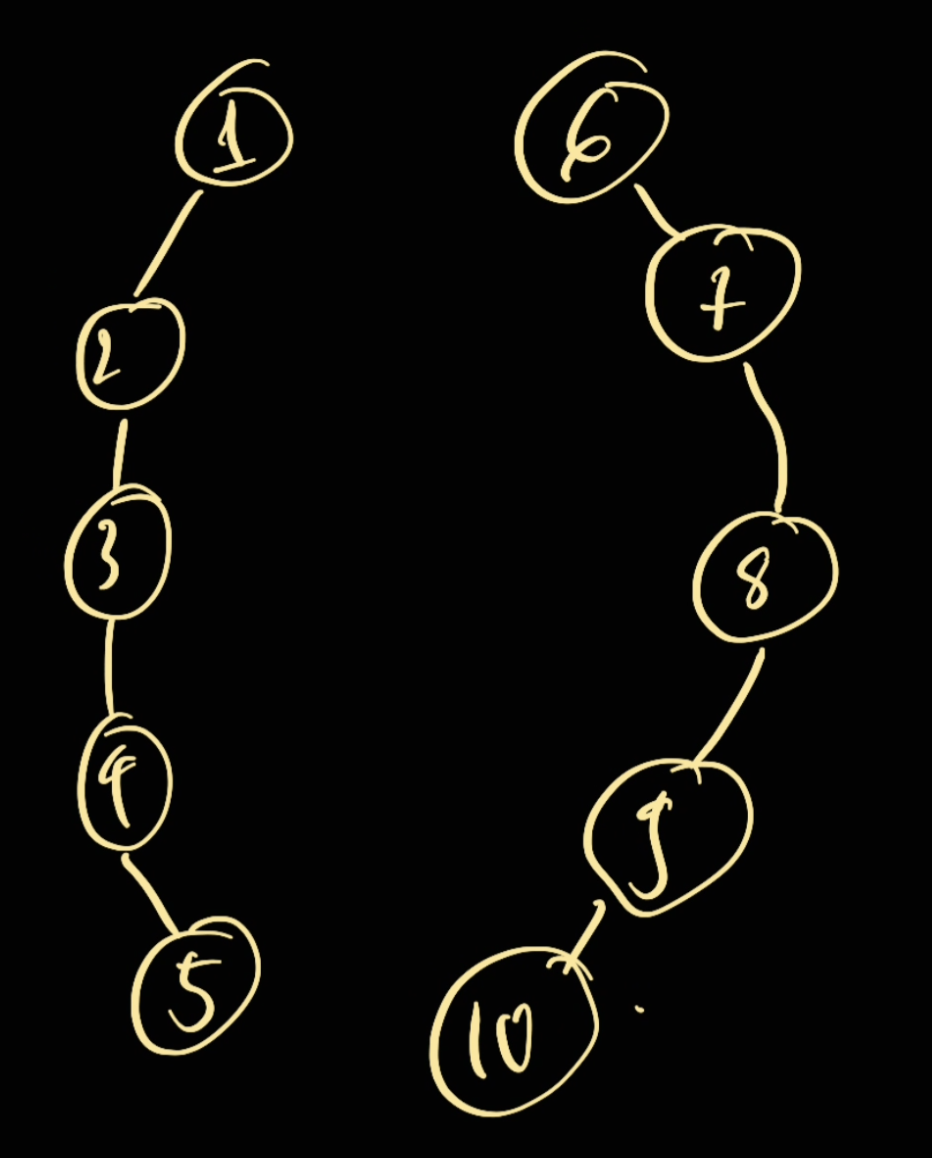
Given the above graph, we have:
find(5) -> 1find(10) -> 6
Implementation
Iteratively
def find(self, node: int):
currNode = node
while currNode != self.parents[currNode]:
parent = self.parents[currNode]
currNode = parent
return currNode
Time complexity: — worst case
Recursively
def find(self, node: int):
if node != self.parents[node]:
return self.find(self.parents[node])
return node
Time complexity: — worst case
Space complexity: — Recursion space
Path compression
As we can see from the above, the path are not optimal in find — to travel from 5 to 1 we need to go through 5 -> 4 -> 3 -> 2 -> 1
As the result, we can compress the path to be as following:
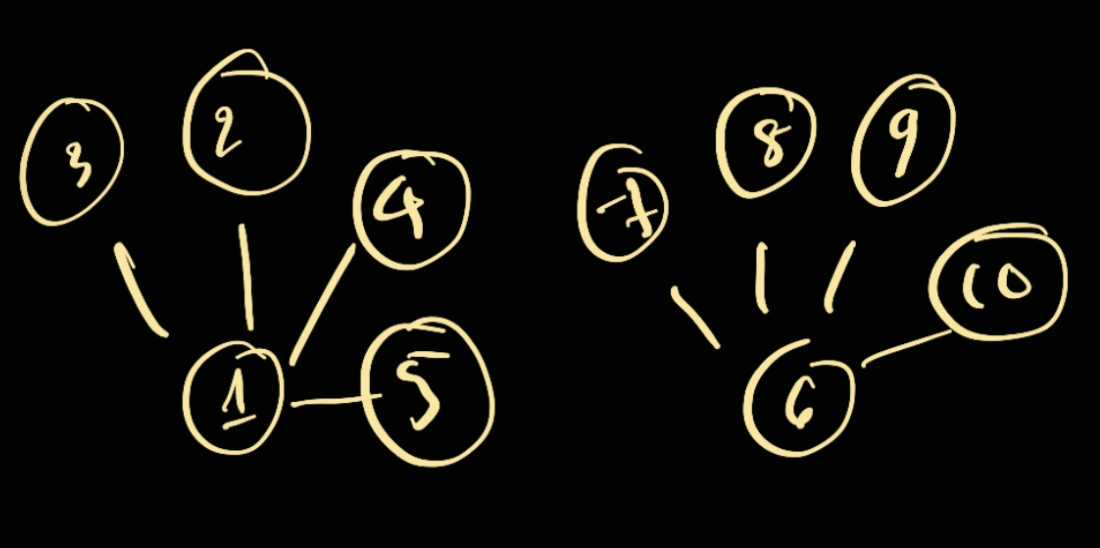
So in this case, travel from 5 -> 1 takes 5 -> 1.
Intuition
The idea is we connect the root of one node to be the root of other node. For example
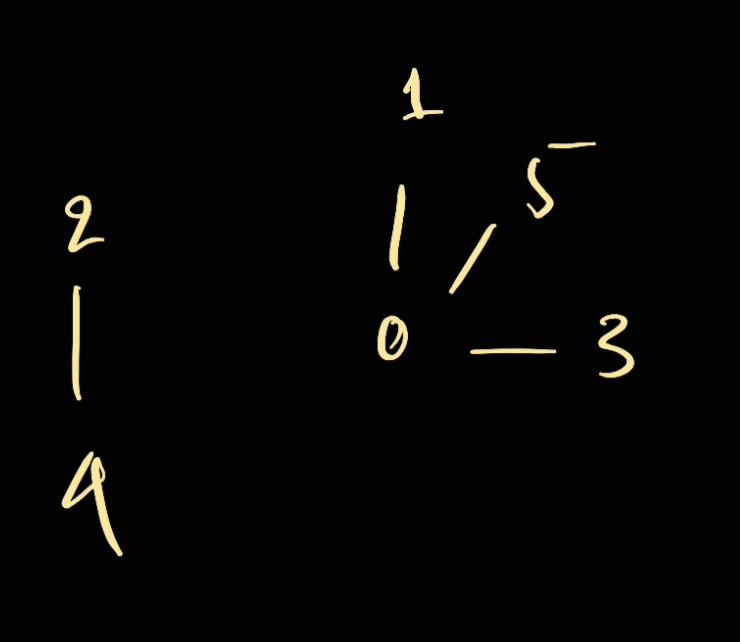
If we now perform union(4, 5) we will:
- Find the root of
4:find(4) -> 2 - Find the root of
5:find(5) -> 0
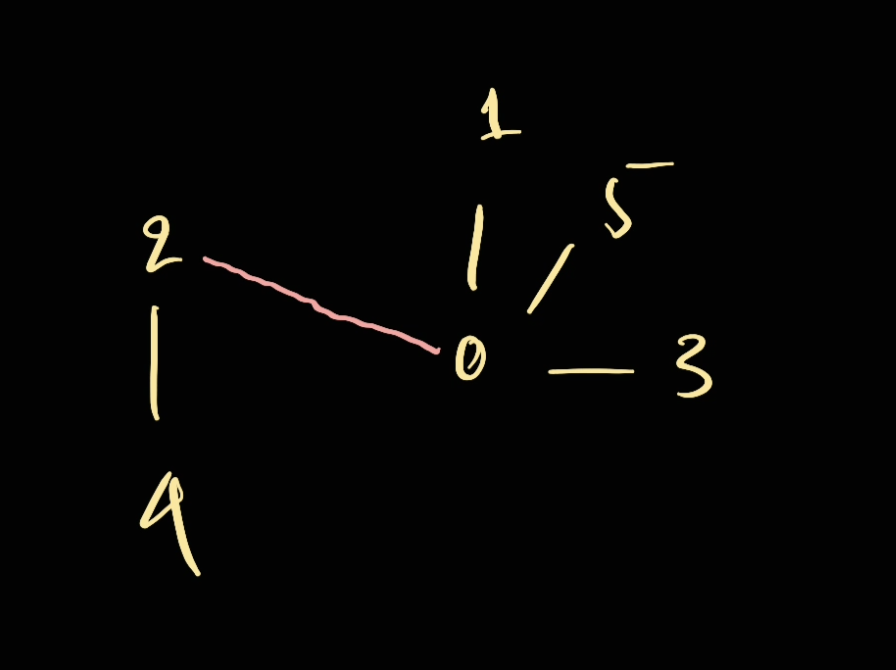
We connect 2 -> 0.
If we continue to do union(4, 1). We first:
find(4) -> 0find(1) -> 0
Since they're the same root, we're not doing union. However, we will compress the path:
- Parent of
4:2- Since
4 != 2.- Assign parent of
4to parent of2:0
- Assign parent of
- We now check
2
- Since
- Parent of
2is0- Since
2 != 0- Assign parent of
2to parent of0:0
- Assign parent of
- We now check
0
- Since
- Parent of
0is0: We break
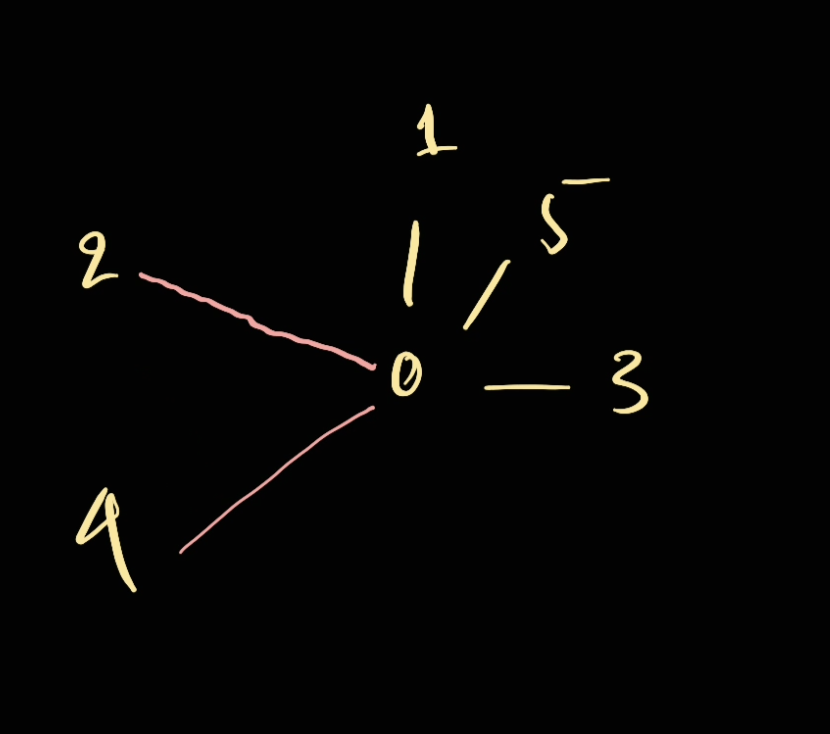
Pseudo
The algorithm works as following:
Assign as we go
while node != parentNode:
assign its parentNode to be the next parent
node -> parentNode
Since algorithm seems like it doesn't work if the tree has more than 3 elements — since assigning to the nextParent might not be sufficient enough.
However if we runs this algorithm from the start, it becomes correct as it always make sure that the nextParent's parent would be the root.
Time complexity:
- The reason why it's is because we traverse the tree upwards.
Simpler way: find root and then assign
root = node
# Find the root
while (root != self.parents[root]):
root = self.parents[root]
# Assign everything to its root
while (node != root):
parent = self.parents[node]
self.parents[node] = root
node = parent
Time complexity:
Implementation
class UnionFind:
def __init__(self, n) -> None:
self.parents = [i for i in range(0, n)]
self.componentSize = [1] * n
def union(self, a: int, b: int) -> bool:
rootA = self.find(a)
rootB = self.find(b)
if rootA == rootB:
return False
if self.componentSize[rootA] < self.componentSize[rootB]:
self.parents[rootA] = self.parents[rootB]
self.componentSize[rootB] += self.componentSize[rootA]
self.componentSize[rootA] = 0
else:
self.parents[rootB] = self.parents[rootA]
self.componentSize[rootA] += self.componentSize[rootB]
self.componentSize[rootB] = 0
return True
def find(self, node: int):
root = node
while (root != self.parents[root]):
root = self.parents[root]
# Path compression
while (node != root):
parent = self.parents[node]
self.parents[node] = root
node = parent
return root
Note that the path compression can also be implemented as follows:
def find(self, node: int):
currNode = node
while (currNode != self.parents[currNode]):
parent = self.parents[currNode]
self.parents[currNode] = self.parents[parent]
currNode = parent
return currNode
Or recursively:
def find(self, node: int):
if node != self.parents[node]:
self.parents[node] = self.find(self.parents[node])
return self.parents[node]
Deal with custom data type
In the example above, we can see that our UnionFind only works with integer as the input. However they might give us a Node or something.
In that case, we might wanna change our datastructures from array to dictionaries
class Node:
def __init__(self, val: str) -> None:
self.val = val
def __repr__(self) -> str:
return self.val
class UnionFindNode():
def __init__(self) -> None:
self.parents = {}
self.componentSize = defaultdict(lambda: 1)
def union(self, a: int, b: int) -> bool:
rootA = self.find(a)
rootB = self.find(b)
if rootA == rootB:
return False
if self.componentSize[rootA] < self.componentSize[rootB]:
self.parents[rootA] = self.parents.get(rootB, rootB)
self.componentSize[rootB] += self.componentSize[rootA]
self.componentSize[rootA] = 0
else:
self.parents[rootB] = self.parents.get(rootA, rootA)
self.componentSize[rootA] += self.componentSize[rootB]
self.componentSize[rootB] = 0
return True
def find(self, node: Node):
currNode = node
while (currNode != self.parents.get(currNode, currNode)):
parent = self.parents.get(currNode, currNode)
self.parents[currNode] = self.parents.get(parent, parent)
currNode = parent
return currNode
if __name__ == "__main__":
unionFind = UnionFindNode()
n1 = Node("1")
n2 = Node("2")
n3 = Node("3")
n4 = Node("4")
n5 = Node("5")
unionFind.union(n1, n3)
unionFind.union(n4, n1)
unionFind.union(n5, n2)
unionFind.union(n2, n3)
print(unionFind.parents, unionFind.componentSize)
Output:
{3: 1, 4: 1, 2: 5, 5: 1} {1: 5, 3: 0, 4: 0, 5: 0, 2: 0})