Number Of Connected Component In A Graph

Question

591 · Connecting Graph III - LintCode

Given n nodes in a graph, denoted 1 through n. ConnectingGraph3(n) creates n nodes, and at the beginning there are no edges in the graph.

You need to support the following method:

1. connect(a, b), an edge to connect node a and node b
2. query(), Returns the number of connected component in the Graph Traversal

Example 1:

Input:
ConnectingGraph3(5)
query()
connect(1, 2)
query()
connect(2, 4)
query()
connect(1, 4)
query()

Output:[5,4,3,3]

Example 2:

Input:
ConnectingGraph3(6)
query()
query()
query()
query()
query()


Output:
[6,6,6,6,6]

Solution

DFS way

This problem can be solve the using the same technique as Number of Islands.

For example in here:

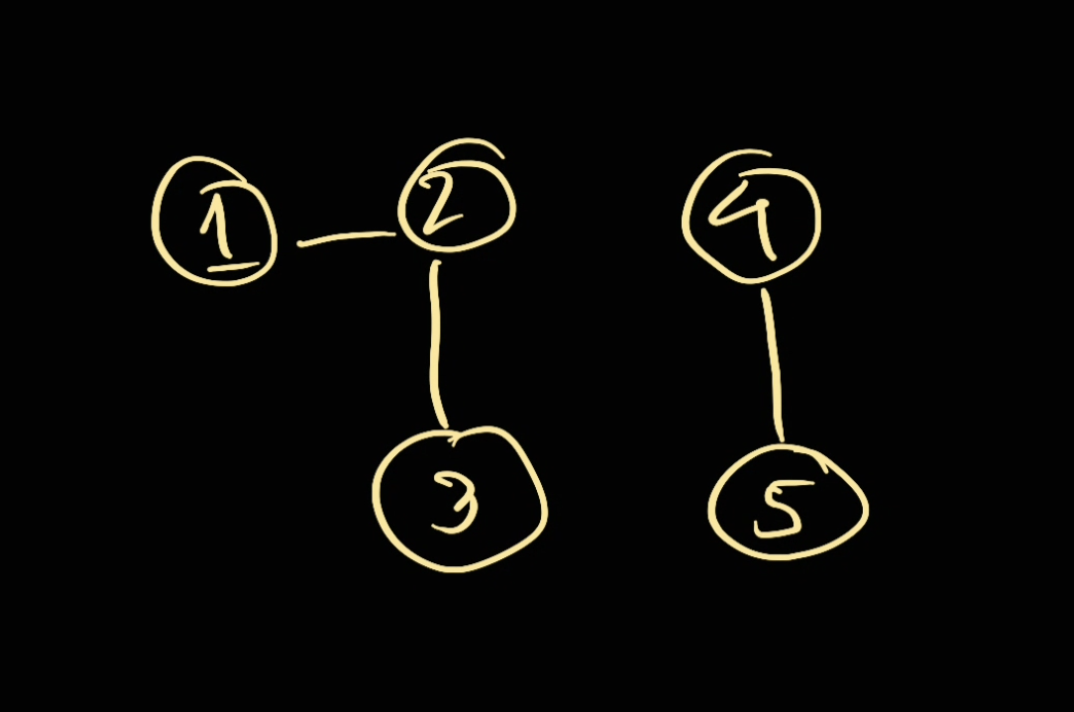
We can just simply go from 1 node (for example 1) and mark everything as visited:

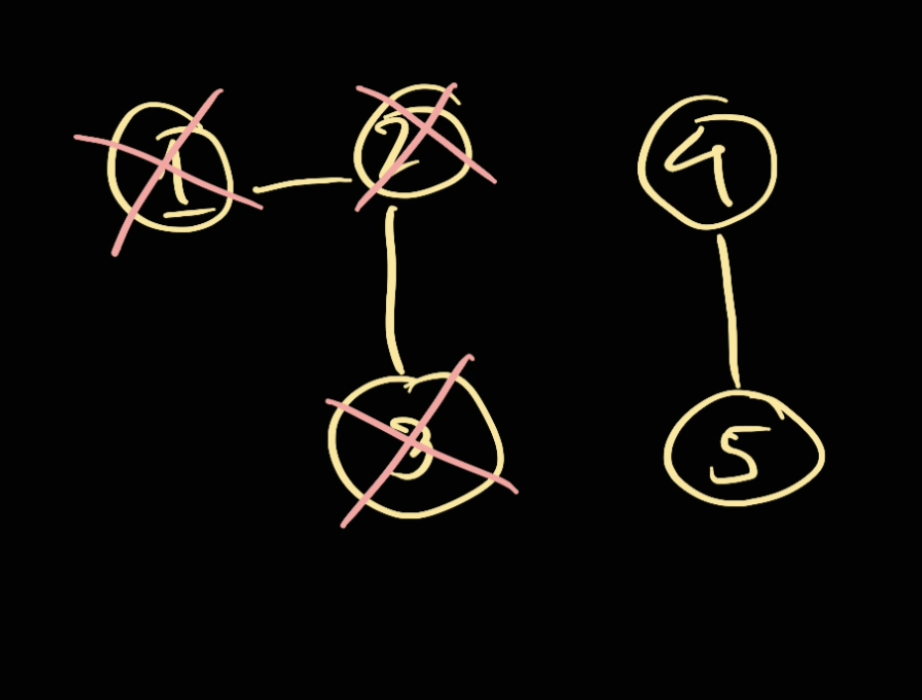
After that, we can increment the count by 1.

We do the same thing for 4:

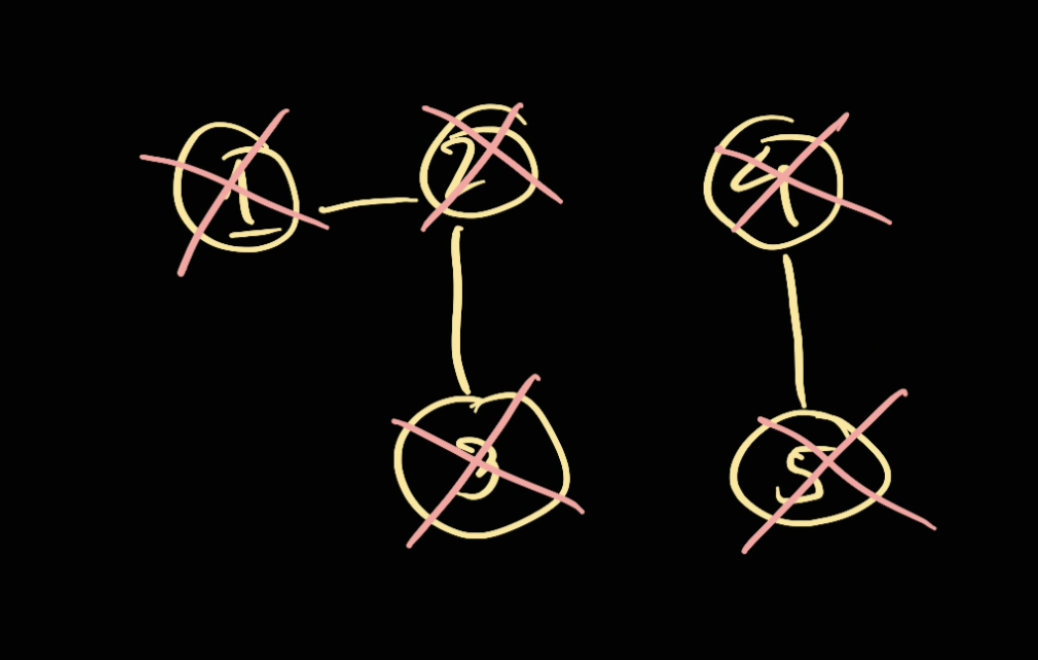
Therefore, the number of connected components is now 2

Implementation

from typing import *
from collections import defaultdict

class ConnectingGraph3:
    n: int
    adjacencyList: Dict[int, List[int]]
    
    def __init__(self, n):
        self.n = n
        self.adjacencyList = defaultdict(lambda: [])

    def connect(self, a, b):
        self.adjacencyList[a].append(b)
        self.adjacencyList[b].append(a)

    def query(self) -> int:
        count = 0
        visited = set()
        for node in range(1, self.n + 1):
            if node in visited: continue
            visited.add(node)

            self.visitGroup(node, visited)
            count += 1
        
        return count
    
    def visitGroup(self, node: int, visited: Set):
        toVisit = [node]
        
        while toVisit:
            currNode = toVisit.pop()
            for neighbour in self.adjacencyList[currNode]:
                if neighbour in visited: continue
                
                toVisit.append(neighbour)
                visited.add(neighbour)

Time complexity: $O(|V| + |E|)$ — $|V|$ is the number of node (n) and $E$ is the number of connected edge (connect)

Space complexity: $O(|V| + |E|)$ — We have to maintain $|E|$ adjacencyList and $|V|$ for the BFS traversal.

Note:

• In here we use the concept of Adjacency List to create our graph for simplicity instead of creating a node class.
• In the query, we count from 1 to self.n + 1 because that's just how they test the query from 1 to n

Union Find way

We can also use Union Find to tackle this problem. So we keep track of numberOfComponent and minus 1 for every single successful union operation.

Implementation

class AppUnion:
    def __init__(self, n): 
        self.unionFind = UnionFind(n)
        self.numberOfComponent = n

    def connect(self, a, b):
	    # Since for this question we count from `1`,
	    # And our [[Union Find]] counts from `0`
	    # We're minusing 1 for both `a`, and `b`
        success = self.unionFind.union(a - 1, b - 1)
        if success: 
            self.numberOfComponent -= 1

    def query(self) -> int:
        return self.numberOfComponent

Time complexity: $O(nlogn)$ — as explained in Union Find
Space complexity: $O(n)$ — to store Union Find parents and number of elements