Graph Valid Tree

178 · Graph Valid Tree - LintCode

Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether these edges make up a valid tree.

You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

Example 1:

Input: n = 5 edges = [[0, 1], [0, 2], [0, 3], [1, 4]]
Output: true.

Example 2:

Input: n = 5 edges = [[0, 1], [1, 2], [2, 3], [1, 3], [1, 4]]
Output: false.

Solution

DFS way

Intuition

One thing that you could think of is to go through all the pairs of edges and check if we've used both pairs or not. However, it's not necessary for edges to contain all the pair. It could have some missing pairs as well. Therefore dependent on the edges will not be a correct answer.

For this question, we need to go through to visit the graph by ourselves just to double check if there is no cycle. Which is similar to Number Of Connected Component in a graph > DFS way

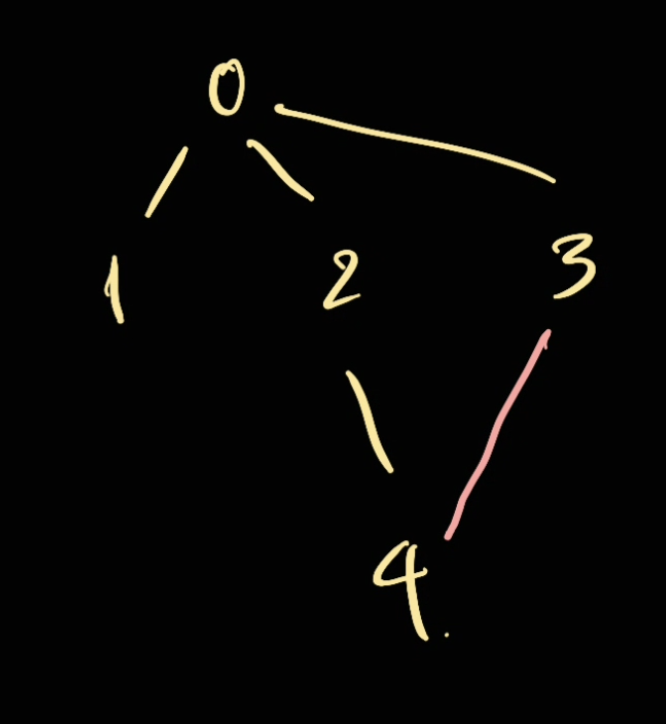
In this following graph, for example if we're at node 4, we want to check all the possible neighbours to see if we can have a cycle.

In this case we can go 2 or 3. However, since 4 is rooted from 2, we should skip 2.

Implementation

Using the concept of Adjacency List, we have:

from typing import *
from collections import defaultdict

class App:
    adjGraph: Dict[int, List[int]]

    def valid_tree(self, n: int, edges: List[List[int]]) -> bool:
        self.adjGraph = defaultdict(lambda: [])
        
        for a, b in edges:
            self.adjGraph[a].append(b)
            self.adjGraph[b].append(a)
        
        visited = set()

        return self.visit(0, None, visited) and len(visited) == n

    def visit(self, node: int, parent: int, visited: Set[int]):
        if node in visited: return False
        
        visited.add(node)
        
        for neighbour in self.adjGraph[node]:
            if neighbour != parent:
                if not self.visit(neighbour, node, visited):
                    return False
        
        return True

Time complexity: $O(|V| + |E|)$

• $|E|$ number of nodes
• $|V|$ number of edges

Space complexity: $O(|V| + |E|)$ — because of the recursion depth

Union Find way

For this one, we can also use Union Find to check if we have a valid edges.

We follows these following steps

1. Every single pair of edges, we will perform a union() of the 2 edges.
2. If the union()
   • not successful (they have the same root), then we should return False
   • successful, then we going to do n -= 1 to keep track the number of disconnected components.
3. We return True if n == 1 (as a result in the end it should only have 1 tree)

class AppUnionFind:
    def valid_tree(self, n: int, edges: List[List[int]]) -> bool:
        unionFind = UnionFind(n)
        numberOfComponents = n
        
        for a, b in edges:
            success = unionFind.union(a, b)
            if (success):
                numberOfComponents -= 1
            else:
                return False
        
        return numberOfComponents == 1

Time complexity: $O(logn)$
Space complexity: $O(logn)$