Unique Paths

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1

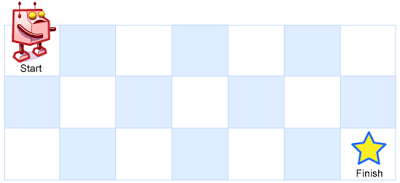
Input: m = 3, n = 7
Output: 28

Example 2

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Intuition

For example if we have a board here and need to calculate the unique moves from A to B:

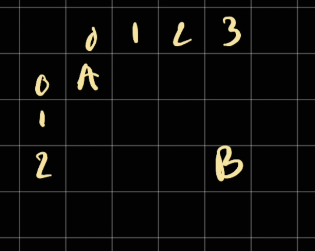
We can work from B to A since at B we know the goal already

As it can be seen from B, we can move to 2 two cells around with 1 unique move:

So the what would be the values at the ?. Since we can only move down and right. It should be the value of down and right.

So should be 2

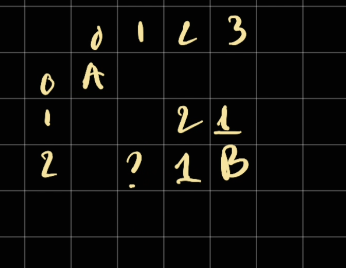
Similarly, in here we can only move down and right. Since we cannot move down, we only take the one from the right. There fore it's 1

In here, since you can go to it by moving down and right. On the right there are 2 ways to move to it, on the bottom there is 1 way to move to it. Therefore it should be 3

So we have the formular

$$ dp[row][col] = dp[down] + dp[right] $$
Or the same as
$$ dp[row][col] = dp[row + 1][col] + dp[row][col + 1] $$

BFS way (Slower)

An obvious way to think of this is to do BFS. Suppose we start from these cells

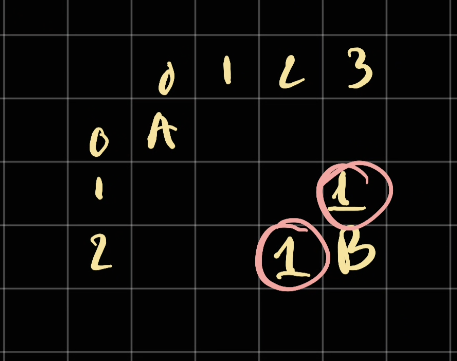
We can then start expanding out:

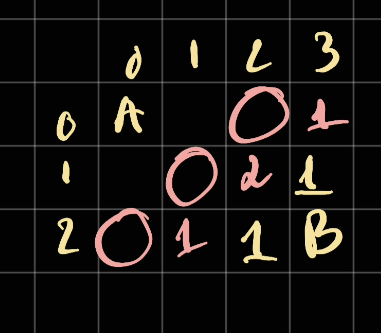
And then continue.

Implementation

Here we can use a queue and pop level by level so that we make sure we have the bottom and the right before we calculate

class AppSlow:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0 for _ in range(n)] for _ in range(m)]

        startPoint = (m - 1, n - 1)
        queue = deque([startPoint])
        visited = set()

        while queue:
            for _ in range(len(queue)):
                currentPosition = queue.popleft()
                visited.add(currentPosition)

                row, col = currentPosition

                if self.isInitialPosition(dp, currentPosition):
                    dp[row][col] = 1
                else:
                    dp[row][col] = self.getPaths(dp, row, col)
                
                for dr, dc in [(-1, 0), (0, -1)]:
                    newRow, newCol = row + dr, col + dc

                    if self.withinBoundary(dp, newRow, newCol) and \
                        (newRow, newCol) not in visited:
                        queue.append((newRow, newCol))
        return dp[0][0]

    def withinBoundary(self, dp, newRow, newCol):
        return newRow >= 0 and newCol >= 0 and newRow < len(dp) and newCol < len(dp[0])

    def isInitialPosition(self, dp, currentPosition):
        row, col = currentPosition
        goalRow, goalCol = len(dp) - 1, len(dp[0]) - 1

        return (row == goalRow and col == goalCol) or\
               (row == goalRow - 1 and col == goalCol) or\
               (row == goalRow and col == goalCol - 1)

    def getPaths(self, dp, row, col):
        bottomResult = dp[row + 1][col] if row + 1 < len(dp) else 0
        rightResult = dp[row][col + 1] if col + 1 < len(dp[0]) else 0
        return bottomResult + rightResult

Time complexity: $O(|V| + |E|)$

• in which $|V|$ is the number of nodes ($m \times n$)
• |E| is the number of edges ($m \times (n - 1) + n \times (m - 1)$)

Space complexity: $O(m \times n)$ + $O(m \times n)$

• Store the queue
• Store the dp array

For loop way (Faster)

It's not necessary to do BFS, we can just do it for loop way and loop for each row, and col.

This works because to find an answer of a cell, we only need the bottom and right. Which essentially can be done with a loop.

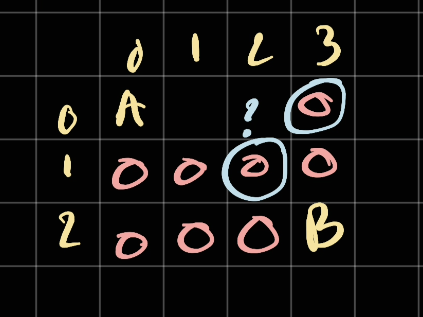
In here if we perform a loop from row to column go reverse, we should already have what we need to calculate ?

Implementation

class App:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0 for _ in range(n)] for _ in range(m)]
        startRow, startCol = (m - 1, n - 1)

        dp[startRow][startCol] = 1
        dp[startRow - 1][startCol] = 1
        dp[startRow][startCol - 1] = 1

        for row in range(startRow, -1, -1):
            for col in range(startCol, -1, -1):
                if dp[row][col] != 0: continue
                bottomRow = dp[row + 1][col] if row + 1 < m else 0
                rightRow = dp[row][col + 1] if col + 1 < n else 0

                dp[row][col] = bottomRow + rightRow
        
        return dp[0][0]

Time complexity: $O(m \times n)$
Space complexity: $O(m \times n)$ — store the dp array

Forward way (Calculate from A)

Similar idea but calculating from A. We need to however calculate the cell of left and top since we move down and right:

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        board = [[0 for col in range(n)] for row in range(m)]

        for row in range(len(board)):
            for col in range(len(board[0])):
                board[row][col] = self.calculateMaximumPath(board, row, col)
        
        return board[-1][-1]
    
    def calculateMaximumPath(self, board: List[List[int]], row: int, col: int):
        if row == 0 and col == 0: return 1

        leftValue = board[row][col - 1] if col > 0 else 0
        topValue = board[row - 1][col] if row > 0 else 0

        return leftValue + topValue