Heap Theory

Theory

Value of a node is ≥ or ≤ than its children depends on if it's min heap or max heap

Binary Heap (Min, Max heap)

• Min-heap will have min at the top
• Max-heap will have max at the top

Two mains operations: insert and extract_min

Insert

Insert at the bottom. Example min-heap:

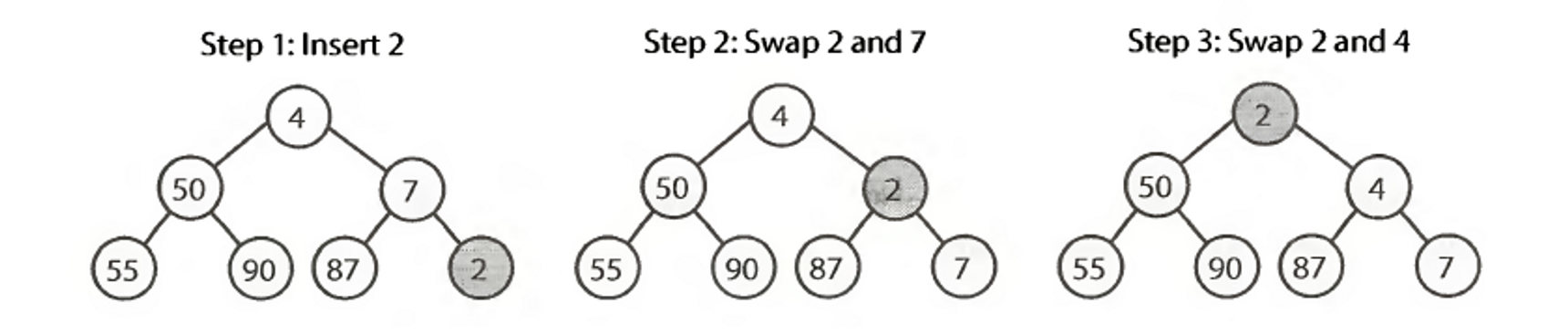
Complexity: O(log n)

Extract

Minimum element is always at the top. We:

1. Remove the top element and swap it with the last element in the heap (bottommost, rightmost element)
2. Sort the heap again from top to bottom

For example in a min-heap:

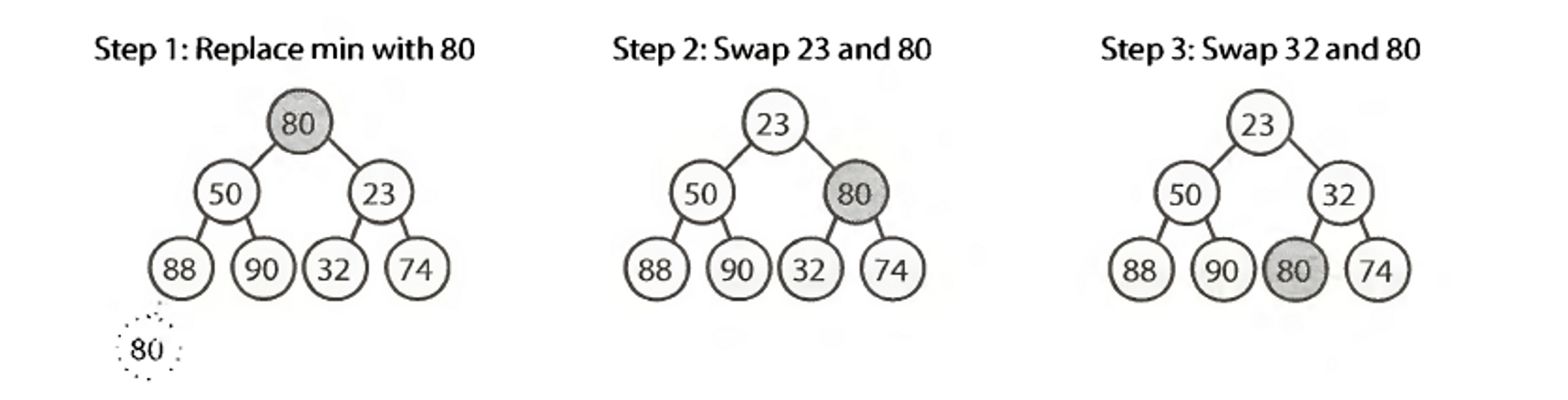
Complexity: O(log n) for building. Popping O(1)

Max nodes at height h

$x = 2^{h+1} - 1$

Get height from number of nodes n

$h = log_2(n)$

In the array

A Heap can be represented as an array. We read the array from top -> bottom and left -> right.

For example this following heap can be read as:

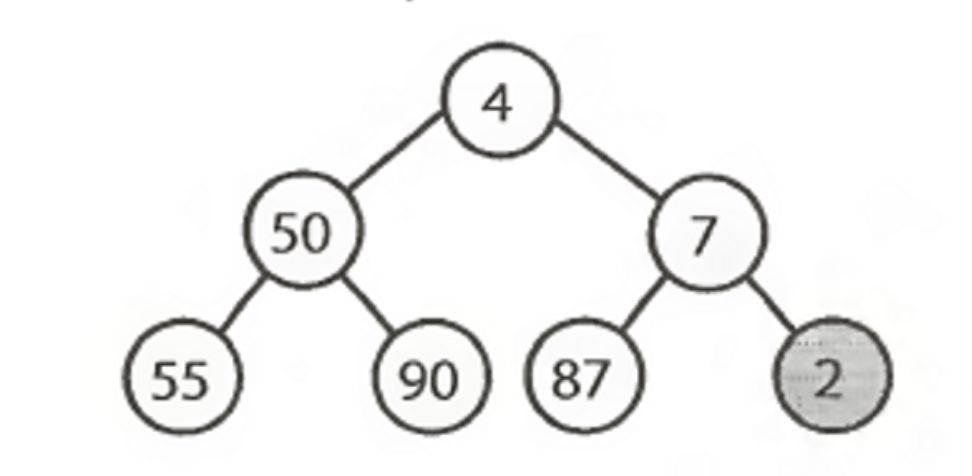
[4,50,7,55,90,87,2]

At index k

1. Its first child is at 2*k + 1.
2. Its second child is at 2*k + 2.
3. Its parent is at (k - 1) // 2.

Tip: just remember the first child, we can figure out the rest.

See: Heap Implementation