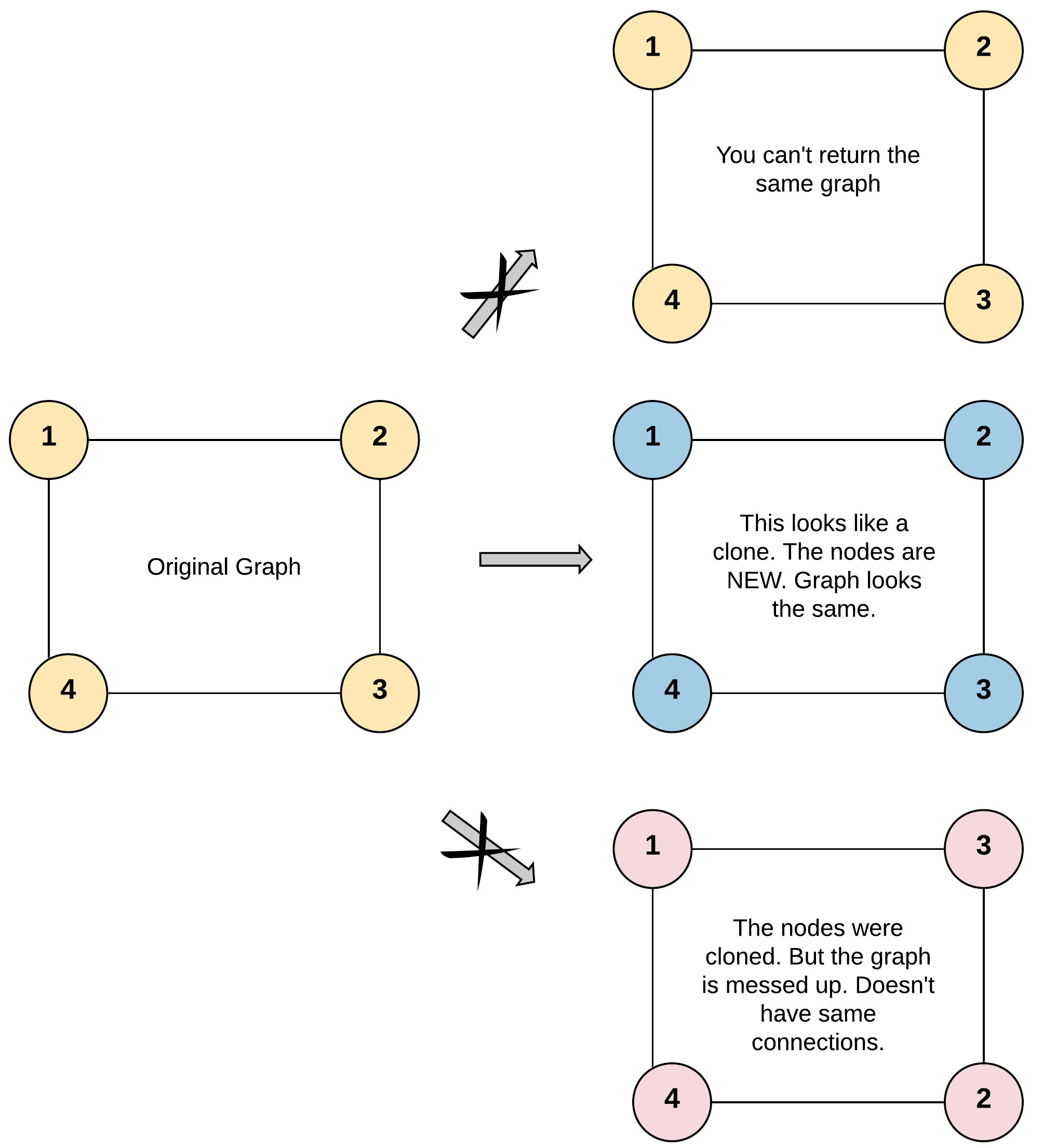
Clone Graph

Question

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Constraints:

• The number of nodes in the graph is in the range [0, 100].
• 1 <= Node.val <= 100
• Node.val is unique for each node.
• There are no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

Solution

We can do a DFS traversal for this question. The reason why we do a DFS is because for each created node, we need to create its neighbors as well. Using BFS would not be able to create the neighbors.

Intuition

For each node, we can go through and then create the neighbors. For each neighbors we recursively doing the same creation.

Looking at this scenario below:

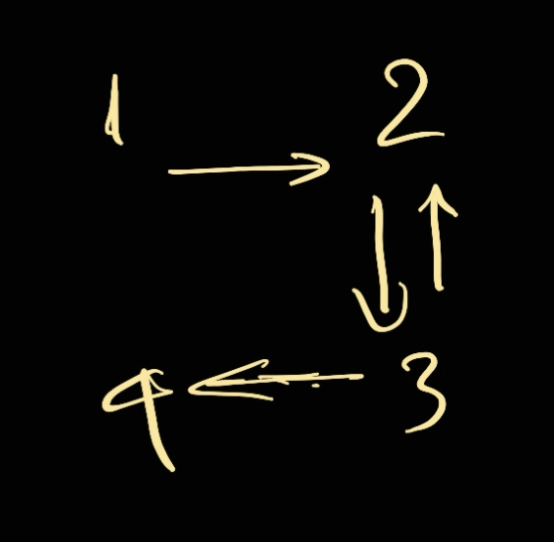
Imagine using recursion, we're now reached to node 4. Since in node 3, we've already added 4 as a neighbors. Because of that, from 4 we need to add 3 as its neighbors as well.

Now for DFS traversal, you will need a visited set. However if 3 is already visited, we need to have a way to return the cloned node 3 that we have already created. Given the constraint is Node.val will be unique, we can do this easily.

Implementation

from typing import *
from collections import deque

class Node:
    def __init__(self, val = 0, neighbors = None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []

class Solution:
    def __init__(self) -> None:
        self.visited = {}

    def cloneGraph(self, node: 'Node') -> 'Node':
        if not node: return None
        if node.val in self.visited: return self.visited[node.val]
        
        clonedNode = Node(node.val)
        self.visited[node.val] = clonedNode
        
        for neighborNode in node.neighbors:
            clonedNeighbour = self.cloneGraph(neighborNode)
            clonedNode.neighbors.append(clonedNeighbour)
            
        return clonedNode

Time complexity: $O(|V| + |E|)$ — since we're doing DFS traversal for each node

Space complexity: $O(|V|)$ — for the vertices that we've created.