Kth Smallest Element In A BST

Question

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) o,f all the values of the nodes in the tree.

Example 1:

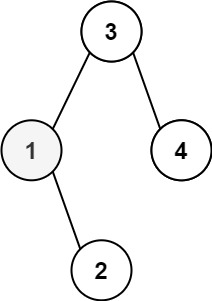
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

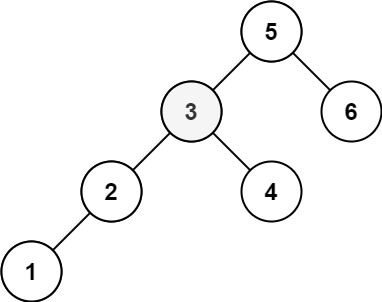
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Solution

We can quickly see that for this problem, we can find the k minimum by looking at the right side of the tree. For example if we have the following:

For example if we're looking for 4th smallest, we can simply traverse from the left to right from the bottom left:

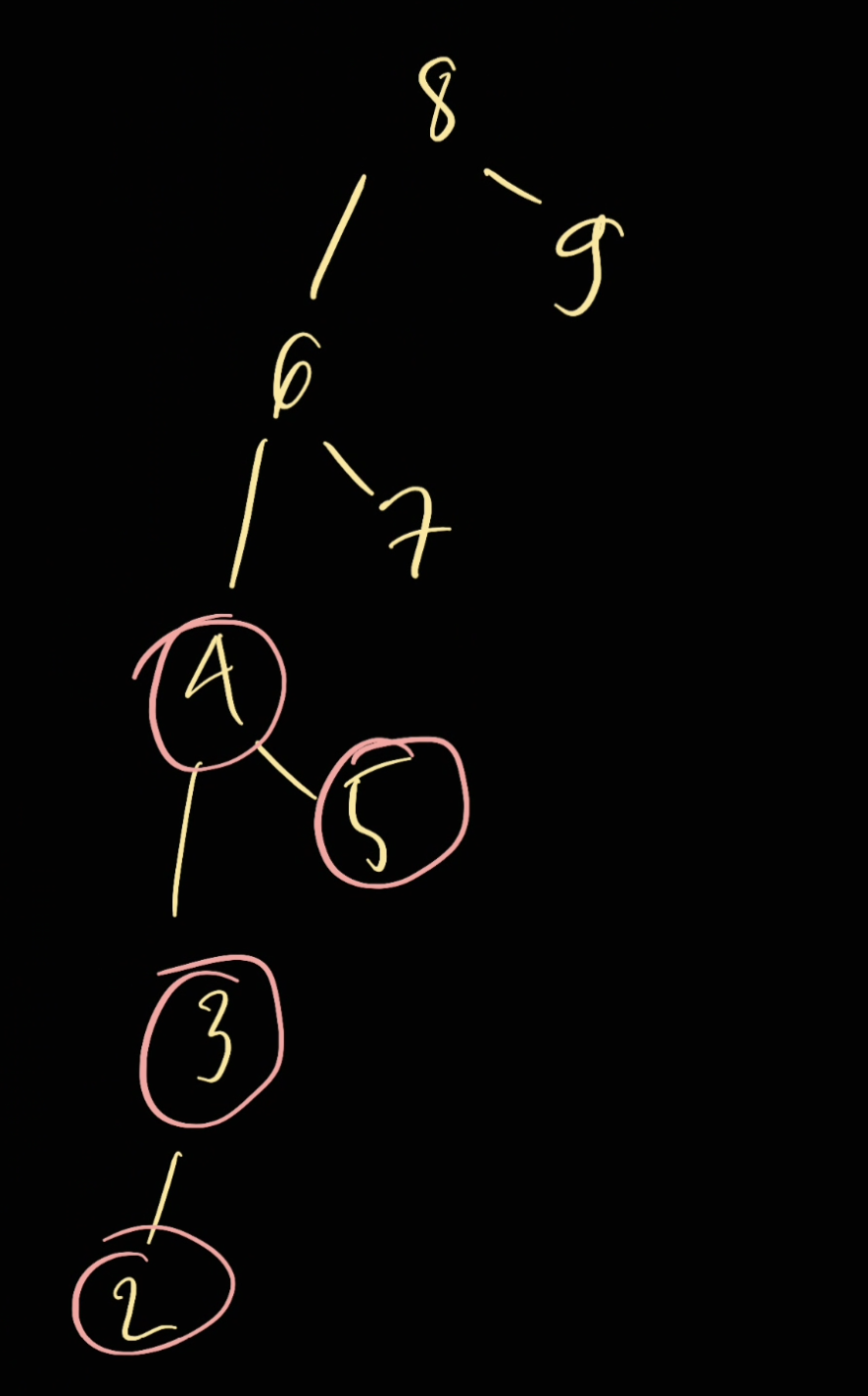
As the result in here we can see that the answer would be 5. In here we can go for an inorder traversal so left -> root -> right.

Recursion or Iterative?

As it's in-order, we have the option of choosing whether it's recursion or iterative. However, choosing it to be recursion will make it harder to break out of the loop once we found the valid solution.

Therefore, we should go for iterative, we can follow in-order traversal iteratively.

Implementation

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int
        if not root: raise Exception("Illegal Arguments")
        stack = []
        currNode = root

        while stack or currNode:
            while currNode.left:
                stack.append(currNode.left)
                currNode = currNode.left
            
            k -= 1
            if (k == 0): return currNode.val

            currNode = stack.pop()
            currNode = currNode.right

        
        raise Exception("No result")

Time complexity: $O(k)$ — given k is the smallest number we're looking for
Space complexity: $O(logn)$ — given that $n$ is the number of nodes inside the tree