Construct Binary Tree From Preorder And Inorder Traversal

Question

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

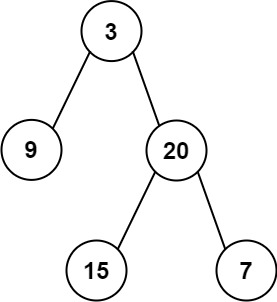
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Solution

Nature of the traversal

To solve this question, we first need to revise inorder traversal and preorder traversal.

In-order traversal

For inorder, we visit the left -> root -> right. This means given an array of inorder traversal, we knows that at one index, whatever on the left handside will be the left elements in the tree. Whatever on the right handside will be the right elements in the tree

For example if we have this tree:

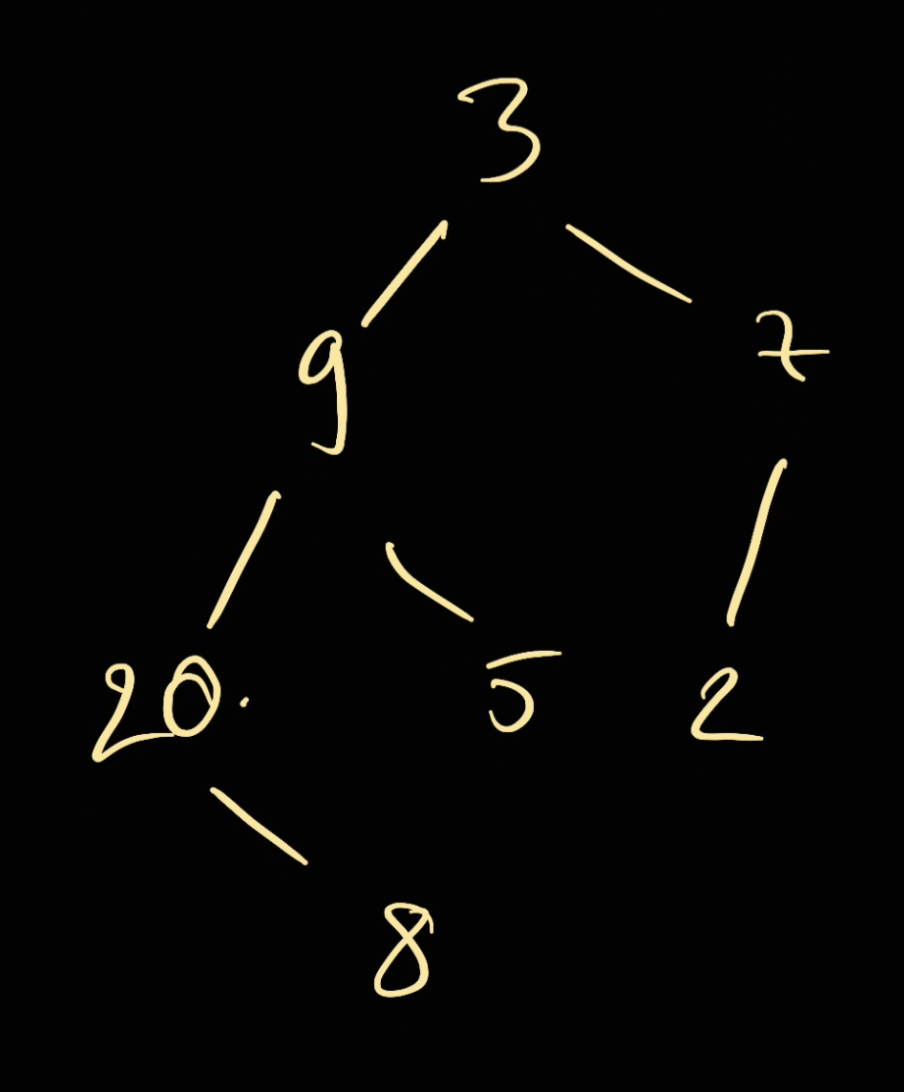
We have our in-order traversal (left -> root -> right) would be:

[20, 8, 9, 5, 3, 2, 7]

So pick 1 point, let say 2:

                 v
[20, 8, 9, 5, 3, 2, 7]
--------left----  -right-

We can see that everything on the left handside of 2: (20, 8, 9, 5, 3) would also appear on the left handside as the tree above. Everything on the right handside of 2 (7) would appear on the right handside in the tree above.

This holds true for any other node as well.

Pre-order traversal

For pre-order traversal, we go root -> left -> right. As a result, we always visit the root first in the order of left -> right. So if we go from left -> right, we should always visit the root first and then its children (and then the right).

Yes it has the right side as well so we need to becareful.

Let revise the example above:

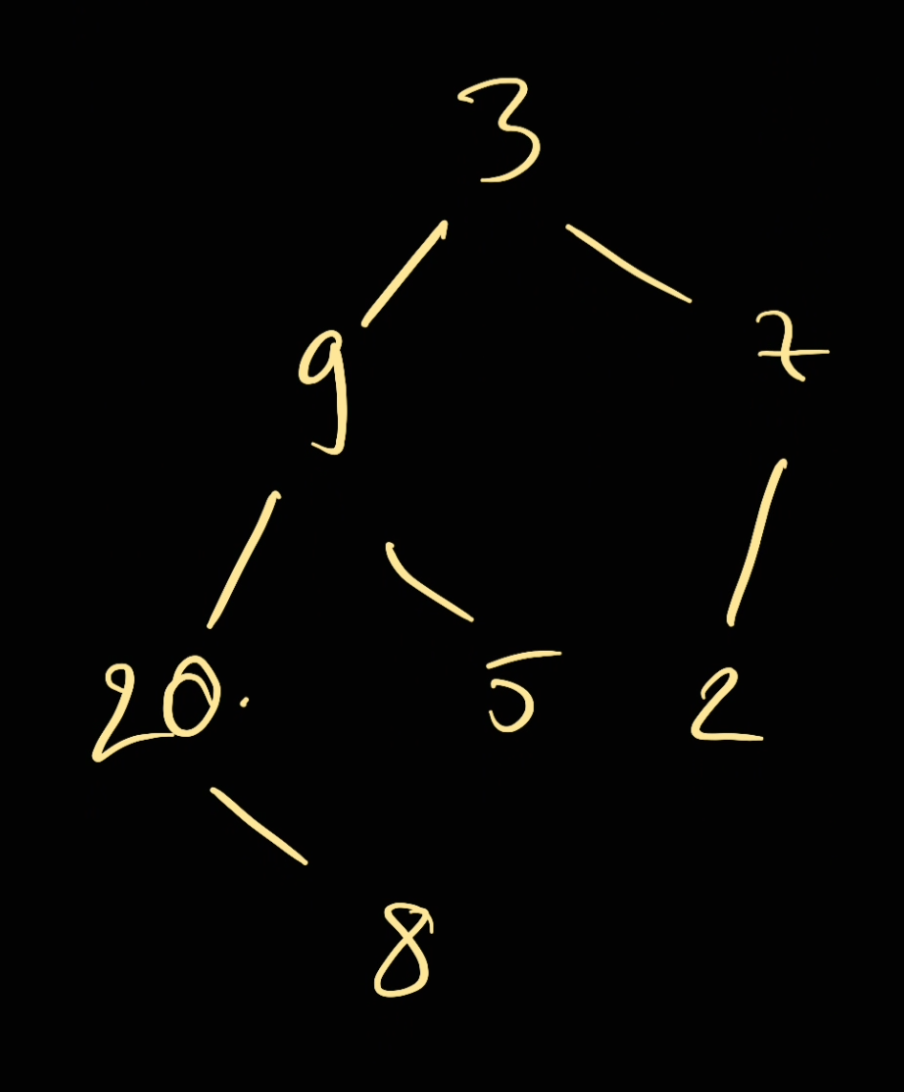
We have our pre-order traversal (root -> left -> right)

[3, 9, 20, 8, 5, 7, 2]

So for example we pick a note in here (20), we can see that 20 is the root of 8 because we visit root and then left and then right.

        v
[3, 9, 20, 8, 5, 7, 2]

However, we don't know if 8 is on our left or on our right. All we know is 20 is the root of 8. Wait, but does that mean 8 is also the root of 5 or 20 is also the root of 5 as well?

[!important]
Yes, we don't know! Sometimes it's the root, sometimes it's just on the right side. So in this case, technically speaking. 20 is either the root of 8 or 8 is just simply on the right side of 20.

So how do we know if it's the root or just on the right side? That's when the in-order comes in.

Considering both in-order and pre-order and try to build the tree out of it.

Let's get the same example above. For example, we have

Preorder: [3, 9, 20, 8, 5, 7, 2]
Inorder: [20, 8, 9, 5, 3, 2, 7]

First, we know for sure 3 is going to be the root of this tree because pre-order traversal will always visit the root first. Therefore we have:

Now based on the Inorder list, we can see that (20, 8, 9, 5) are in the left of 3 whereas (2, 7) are in the right.

              v
[20, 8, 9, 5, 3, 2, 7]
 -----left----   -right-

Therefore, we can conclude this following:

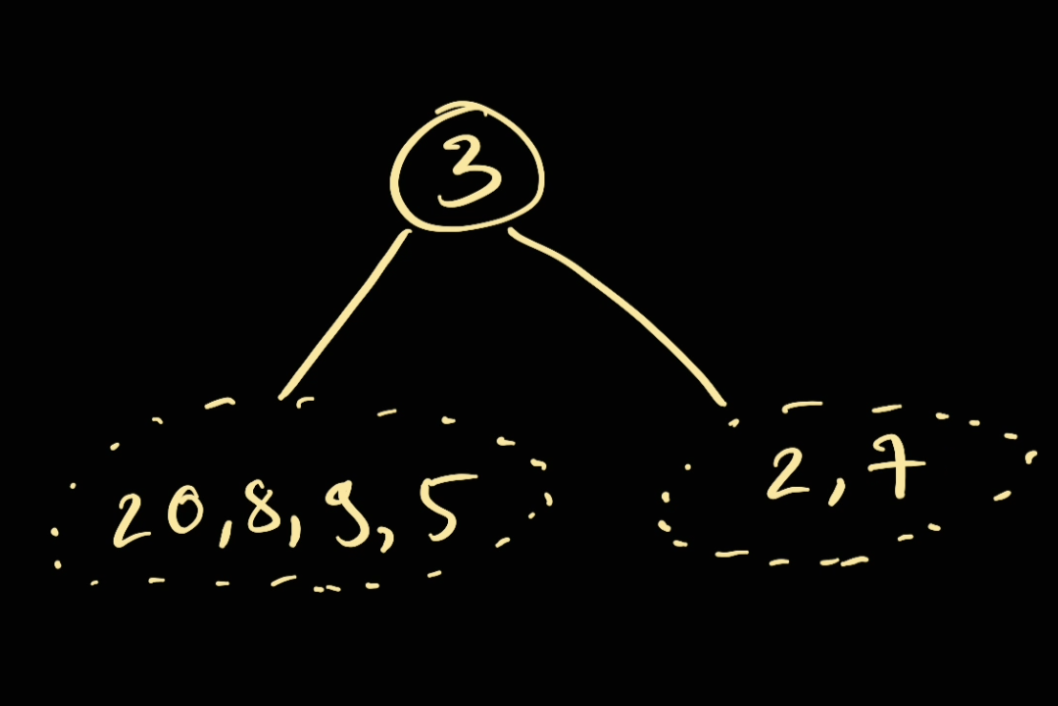
So on the left handside, amongst 20, 8, 9, 5 there one of them should be the next root. Similarly either 2,7 should be the next root.

Let's visit our pre-order list:

[3, 9, 20, 8, 5, 7, 2]

And come back to the previous question:

Wait, but does that mean 8 is also the root of 5 or 20 is also the root of 5 as well?

Well, we can't answer it yet. But if you compare between (5, 7, 2), we know that 7 and 2 will be on the right side of 5

So applying this concept, we just keep digging futher until we know.

Next candidate for our pre-order list is 9. Since 9 is within this list of (20, 8, 9, 5), we conclude that 9 will be the root of all of these numbers.

Now look at this inorder list, we have (20, 8) on the left handside, and (5) will be on the right handside

        v
[20, 8, 9, 5, 3, 2, 7]
 -left-   -r-

So we have

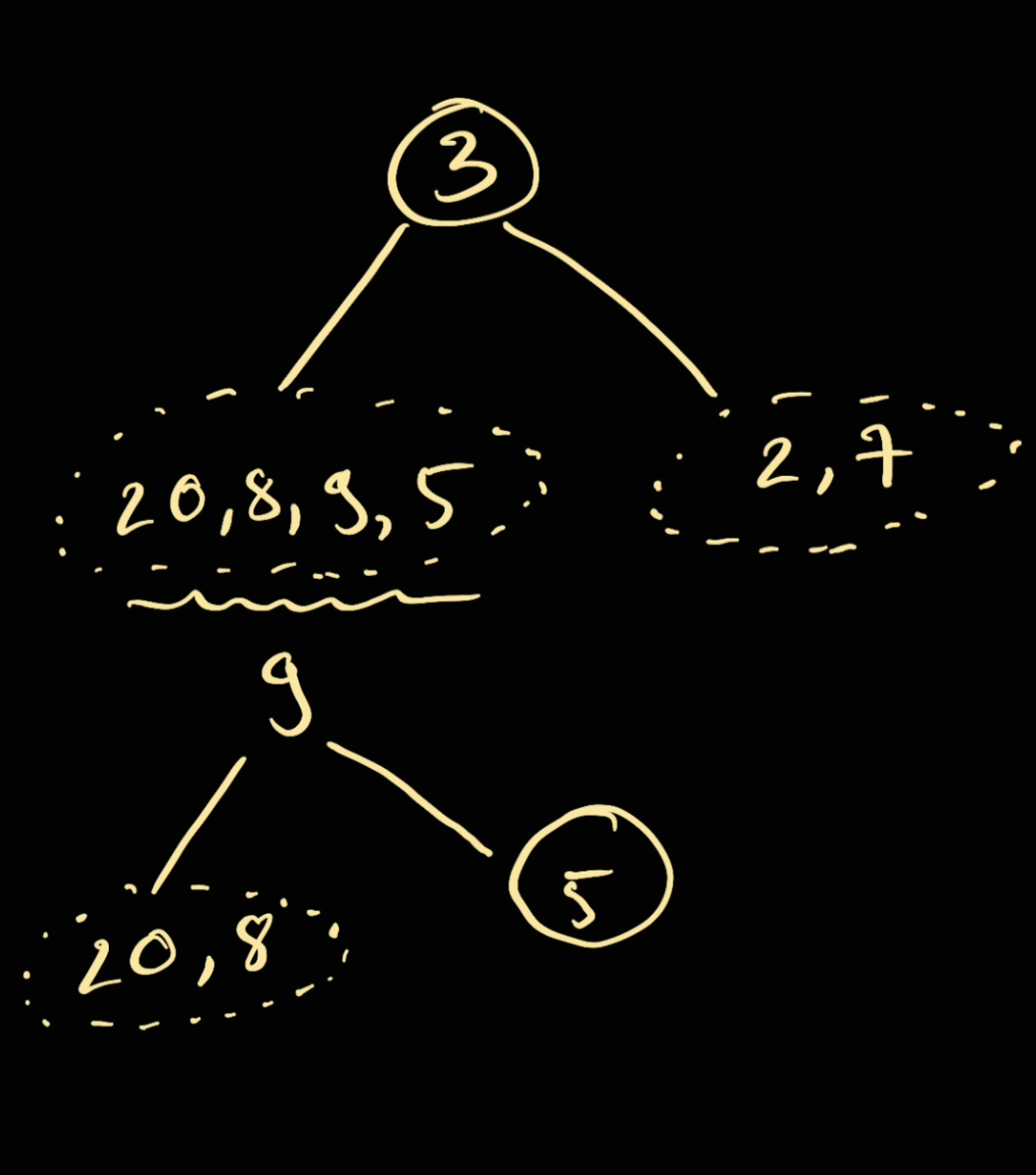
Now we can answer our previous question: no, 8 will not be the root of 5 and neither 20

[!important]
Note: it's important that when we're looking for the root, we only take in consideration the number within our range. So in this case for example in the group of 20, 8.

Preorder: [3, 9, 20, 8, 5, 7, 2]

We should only consider 20, 8 as the root and not 5,7,2 at all. Therefore we need to slice our array of preorder to be only 20, 8.

Implementation

class App:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder or not inorder: return None

        currentRootValue: int = preorder[0] 
        root = TreeNode(currentRootValue)

        indexCurrentRootValue = inorder.index(currentRootValue)
        leftInorder = inorder[:indexCurrentRootValue]
        rightInorder = inorder[indexCurrentRootValue + 1:]

        root.left = self.buildTree(preorder[1 : 1 + len(leftInorder)], leftInorder) 
        root.right = self.buildTree(preorder[1 + len(leftInorder):], rightInorder)

        return root

Time complexity: $O(n^2)$

• Every single element we need to visit 2 array. For every single time need to do an index() that will take $logn$ and slice and so on

Space complexity: $O(n \times n) = O(n^2)$

• For space complexity, we are recursionly loop through 2 branches left, right for each node. And then we also bring our array over (2 arrays of n) element worst case so it's going to be $O(n^2)$

Note: in here as explain above, we only wants to pass the relevant preorder to the subtree. So for example in the case where we have

Preorder: [3, 9, 20, 8, 5, 7, 2]
Inorder: [20, 8, 9, 5, 3, 2, 7]
root = 3
leftInorder = [20, 8, 9, 5]
rightInorder = [2, 7]

Therefore, the possible roots candidate of 7 and 2 should be 7,2. Which is 4 elements (size of the left inorder) away from 3

Optimisation

1. Quick find the length of leftInorder

As we see in the above, the length of leftInorder is len(20, 8, 9, 5) == 4. However another way to find this length is just simply the index of 3:

                     index 4
                       v
Inorder: [20, 8, 9, 5, 3, 2, 7]
          -----------
   there must be 4 elements here

Therefore we can just simply replace len(leftInorder) == indexCurrentRootValue

class App:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder or not inorder: return None

        currentRootValue: int = preorder[0]
        root = TreeNode(currentRootValue)

        indexCurrentRootValue = inorder.index(currentRootValue)

        root.left = self.buildTree(preorder[1 : 1 + indexCurrentRootValue], inorder[:indexCurrentRootValue]) 
        root.right = self.buildTree(preorder[1 + indexCurrentRootValue:], inorder[indexCurrentRootValue + 1:])

        return root

2. Use two pointers to define index instead of slicing and 1 hashmap

As we can see, we can simply optimise by using 2 pointers to define the index with a hashmap to quickly find the index of the element in the array without having to do .index() and slicing.

Therefore we have this following code:

class App:
    preorderIndexMap: Dict[int, int]
    inorderIndexMap: Dict[int, int]

    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        self.preorderIndexMap = { number: index for index, number in enumerate(preorder) }
        self.inorderIndexMap = { number: index for index, number in enumerate(inorder) }
        self.preorder = preorder

        return self._buildTree(0, len(preorder), 0, len(inorder))

    def _buildTree(self, preorderStartIndex, preorderEndIndex, inorderStartIndex, inorderEndIndex) -> Optional[TreeNode]:
        if preorderStartIndex >= preorderEndIndex or inorderStartIndex >= inorderEndIndex: return None

        currentRootValue: int = self.preorder[preorderStartIndex]
        root = TreeNode(currentRootValue)

        indexCurrentRootValue = self.inorderIndexMap[currentRootValue]

        inorderLength = indexCurrentRootValue - inorderStartIndex + 1
        
        root.left = self._buildTree(preorderStartIndex + 1, preorderStartIndex + inorderLength, inorderStartIndex, indexCurrentRootValue)
        root.right = self._buildTree(preorderStartIndex + inorderLength, preorderEndIndex, indexCurrentRootValue + 1, inorderEndIndex)

        return root

Time complexity: $O(n + n) = O(n)$

• For each element to build, we visit twice — one at the preorder list and one at the inorder list

Space complexity: $O(n)$

• To keep track of the index map