Lowest Common Ancestor

Question

Given a binary search tree (BST) | or Binary Tree, find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example

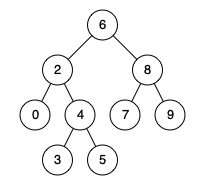
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

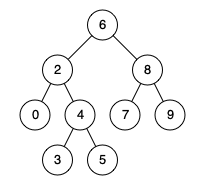
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Input: root = [2,1], p = 2, q = 1
Output: 2

Solution

Given a binary tree (not binary search tree)

We can do a Tree DFS post-order traversal to start looking for the node. For example:

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root: return None
        if (root == p or root == q): return root 

        leftCommonAncesstor = self.lowestCommonAncestor(root.left, p, q)
        rightCommonAncestor = self.lowestCommonAncestor(root.right, p, q)
        
        if leftCommonAncesstor and rightCommonAncestor:
            return root
        
		return leftCommonAncesstor or rightCommonAncestor

The reason why we're doing postorder is because we need to look at the children first before making a decision.

In here, since the element in the tree are unique. We can return if root == p or root == q. So technically root can only equals to one of them because they're unqiue.

We check if in the left we have either node q or p and check in the right if we have the same.

If we have both left and right, we should return root

else we should return leftCommonAncesstor or rightCommonAncestor, the one which is not None will be returned

[!note]
We can do this since the question specifically mentioned that the root will guarantee exists.

So technically we want to priority the top element we found. Therefore we use a postorder traversal

Time Complexity: $O(n)$ because we have to go through all the node one by one
Space Complexity: $O(logn)$ given the recursion, we need to traverse the height of the tree - which is $O(logn)$

Given a binary search tree

For a binary search tree, since left < root < right. It's actually faster and we can achieve $O(logn)$ time complexity.

For this, we can do a pre-order traversal, since we can determine if the root is the lowest common ancestor node without the need to traverse through its children.

Since everything on the right branch > root > everything on the left branch. We can simply do this check at a node to see if it's lowest common ancestor:

 if (root.val <= p.val and root.val >= q.val) or\
	(root.val >= p.val and root.val <= q.val):
		# If root inbetween the 2 values
		return root

There should be only 1 root that valid the above condition. There can't be a situation that some where in the tree there is another root that satisfy the same condition as well.

[!note]
This is because of the nature of binary search that if there is a root that stays in between 2 values. That root is the only root that is between that has 2 values.

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root: return None

        if (root.val <= p.val and root.val >= q.val) or\
            (root.val >= p.val and root.val <= q.val):
                # If root inbetween the 2 values
                return root
        # root has to be either smaller or larger than both value, we can pick either q or p to check
        if root.val > p.val:
            # if root is larger, we need to go to the left
            return self.lowestCommonAncestor(root.left, p, q)
        else:
            # else we go to the right
            return self.lowestCommonAncestor(root.right, p, q)

We can also do this iteratively:

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        currNode = root
        while currNode:
            if (currNode.val <= p.val and currNode.val >= q.val) or\
                (currNode.val >= p.val and currNode.val <= q.val):
                # If currNode inbetween the 2 values
                return currNode
	        # currNode has to be either smaller or larger than both value, we can use 1 to check
            if currNode.val > p.val:
                # if currNode is larger, we need to go to the left
                currNode = currNode.left
            else:
                # else we go to the right
                currNode = currNode.right

Time complexity: $O(logn)$
Space complexity:

• Recursive method: $O(logn)$
• Iterative: $O(1)$