Maximum Depth Of Binary Tree

Question

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

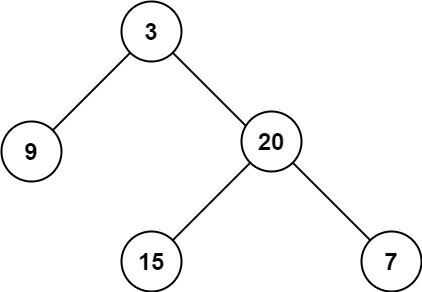
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Solution

For this question we can do either tail or non-tail recursion.

Tail recursion

For tail recursion, we want to keep track of the level and pass it to the children nodes. Therefore we have

class Solution:
    maxDepth: int

    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root: return 0

        self.maxDepth = 0
        self.dfsCountHeight(root, 1)

        return self.maxDepth
    

    def dfsCountHeight(self, node: Optional[TreeNode], level: int) -> None:
        if not node: return

        self.maxDepth = max(self.maxDepth, level)
        
        self.dfsCountHeight(node.left, level + 1)
        self.dfsCountHeight(node.right, level + 1)

Time complexity: $O(n)$ — $n$ is the number of nodes
Space complexity: $O(logn)$ — the height of the binary tree

Non tail recursion

For non-tail recursion, we want to start from the bottom up. So for example given the tree:

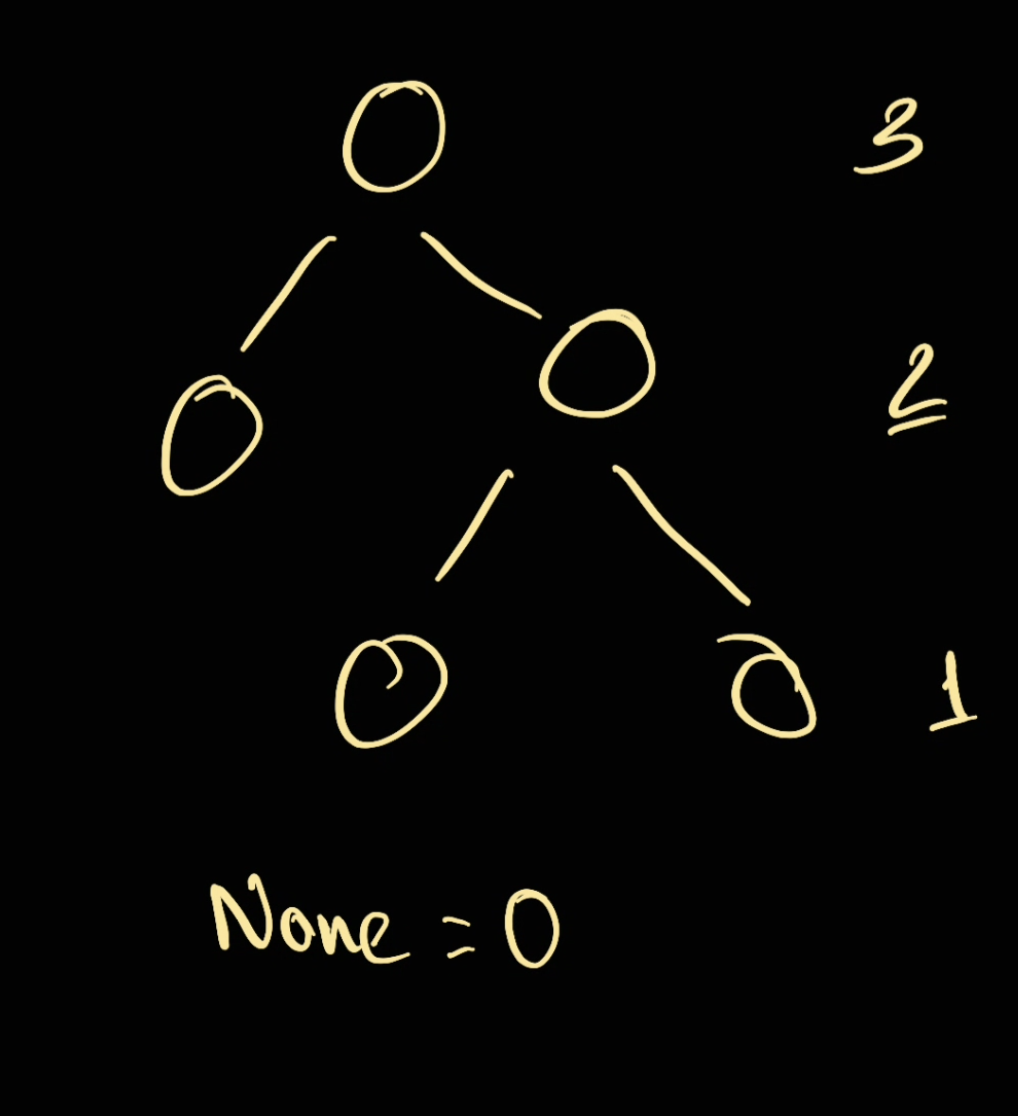
So in our case, we want the root node to return 3. As a result, we want in our base to return 0, so we can populate up to 3 in the root.

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None: return 0
        
        left = self.maxDepth(root.left) + 1
        right = self.maxDepth(root.right) + 1
        
        return max(left,right)

Time complexity: $O(n)$ — $n$ is the number of nodes
Space complexity: $O(logn)$ — the height of the binary tree