Binary Tree Maximum Path Sum

Question

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

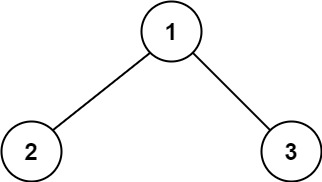
Input: root = [1,2,3]
Output: 6
Explain: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

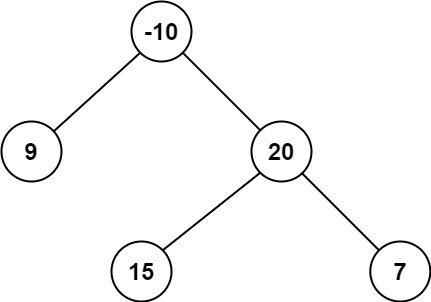
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Solution

In this problem, it's important to work from the sub problem to the bigger problem. So let's start with the very easy sub-problem.

Imagine that the tree is like below, what would be the max sum?

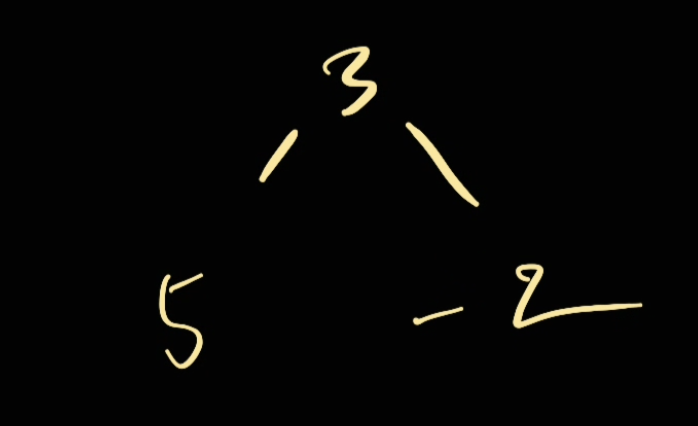
It's going to be 8. The formula can be calculated as following

maxSum = root + max(left, 0) + max(right, 0)

The max() in here is for the case when one of the value is negative. If that so we don't want to take that value anymore.

Now let's imagine if there is something above 3, so like:

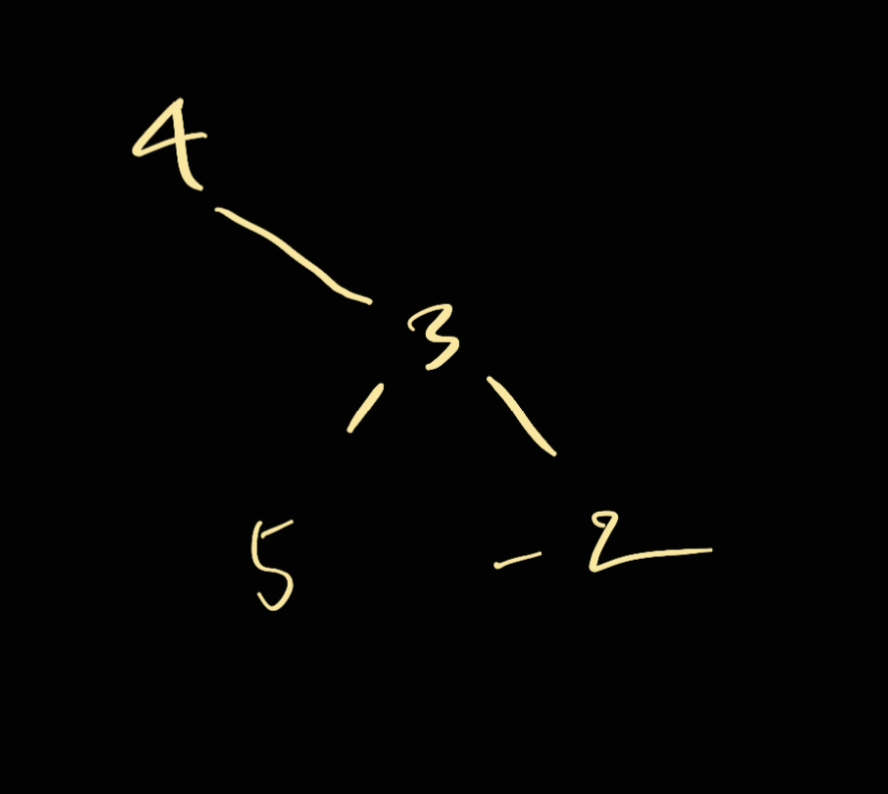
How would you propagate the result back to 4? It should be either

• 5 + 3
• 3 + max(-2, 0) = 3

As a result, we can have this basic recursion logic

maxSum = root + max(left, 0) + max(right, 0)
return max(root + left, root + right)

Implementation

class App(object):
    maxSum: int

    def maxPathSum(self, root: Optional[TreeNode]) -> Optional[int]:
        if not root: return None
        self.maxSum = float('-inf')
        self._maxPathSum(root)
        return self.maxSum

    def _maxPathSum(self, root: Optional[TreeNode]) -> int:
        if not root: return 0

        if not root.left and not root.right: 
            self.maxSum = max(self.maxSum, root.val)
            return root.val

        leftSum = max(self._maxPathSum(root.left), 0)  
        rightSum = max(self._maxPathSum(root.right), 0) 

        self.maxSum = max(leftSum + rightSum + root.val, self.maxSum)
        return max(root.val + leftSum, root.val + rightSum)

Time complexity: $O(n)$

• Given $n$ is the number of nodes inside the tree, we at least need to visit each node once

Space complexity: $O(logn)$

• Because we're doing recursion, so we need to count the memory heap which is the height of the tree