Largest Rectangle In Histogram

Question

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

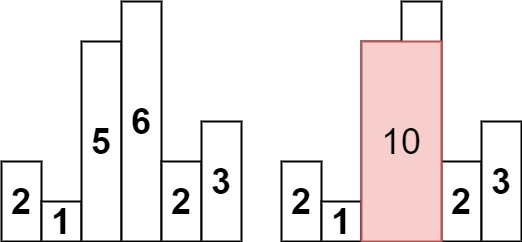
Input: heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1.
The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

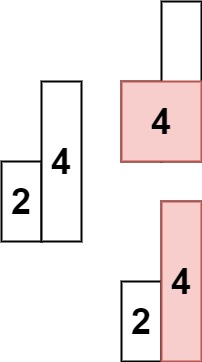
Input: heights = [2,4]
Output: 4

Solution

Bruteforce

Since a histogram is bounded by it's min height. A bruteforce solution is to go through everything to calculate the are with subject to min height:

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        maxArea = float('-inf')

        for i in range(len(heights)):
            minHeight = heights[i]
        
            for j in range(i, len(heights)):
                minHeight = min(minHeight, heights[j])
                width = j - i + 1
                maxArea = max(maxArea, minHeight * width)
        
        return maxArea

Time Complexity: $O(n^2)$
Space: $O(1)$

Monotonic stack O(n)

In this problem, we can use Monotonic Stack to solve this algorithm. Basically we want to build an increasing histogram.

For example, the following is considered an increasing histogram:

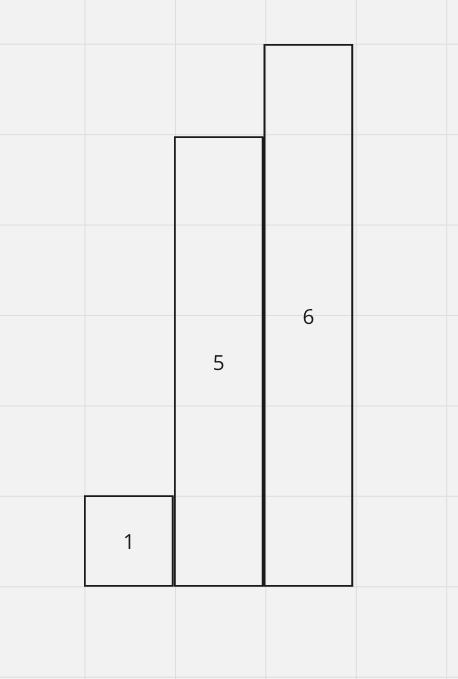
It basically just increasing, not going down.

Why?

Because once we have something like that, we can calculate the maxArea from each the histogram using just for loop:

increasingHistograms = [1,5,6]
maxArea = 0

for i, height in enumerate(increasingHistograms):
    maxWidth = len(increasingHistograms) - i
    maxArea = max(maxArea, maxWidth * height)

print(maxArea) # 10

So how do we do it.

We need to pop out the one that's not increasing so that we have an increasing histogram.

Let's consider this one:

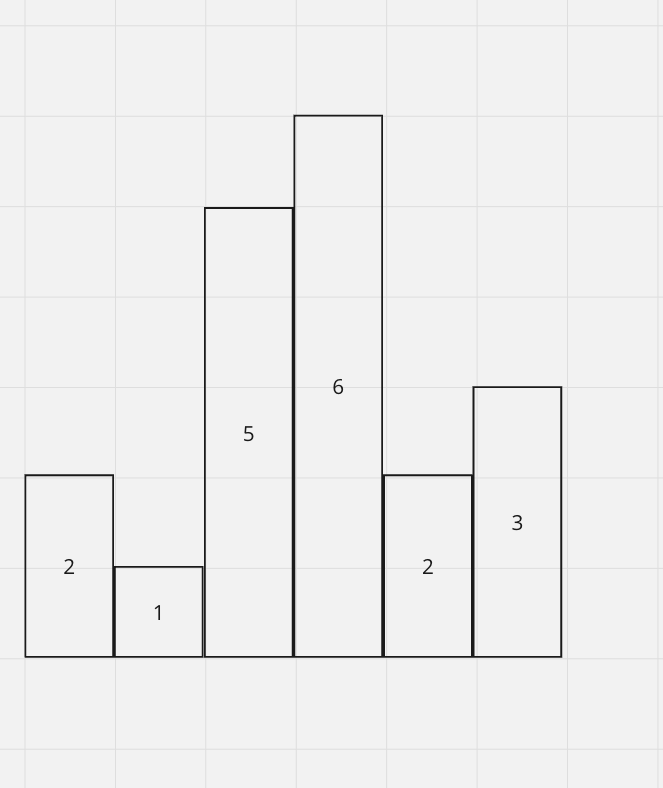
We want to pop out (2,5,6) as we go from left -> right so that our histogram is increasing.

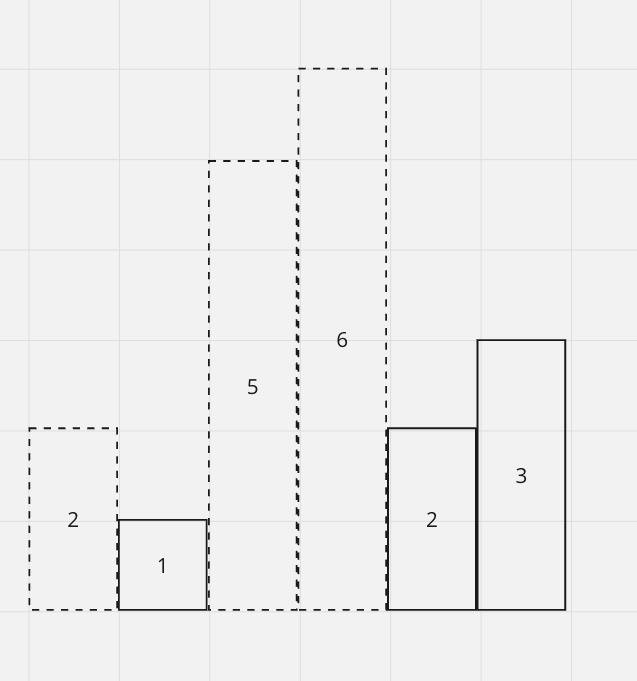
As a result, a histogram of 1, 2, 3 should be increasing.

But what happen to the empty space after we pop? We should extend the rest of our histogram out to use that space.

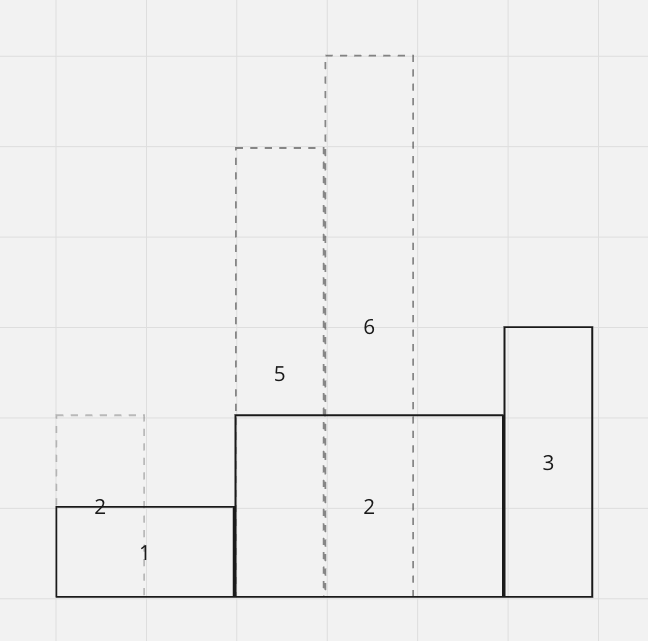
So that's the idea. In the end we can just calculate the maxArea of the graph above to keep track of our maxArea

How ever, we also need to calculate the maxArea of the increasingHistograms that we popped

Algorithm walk through

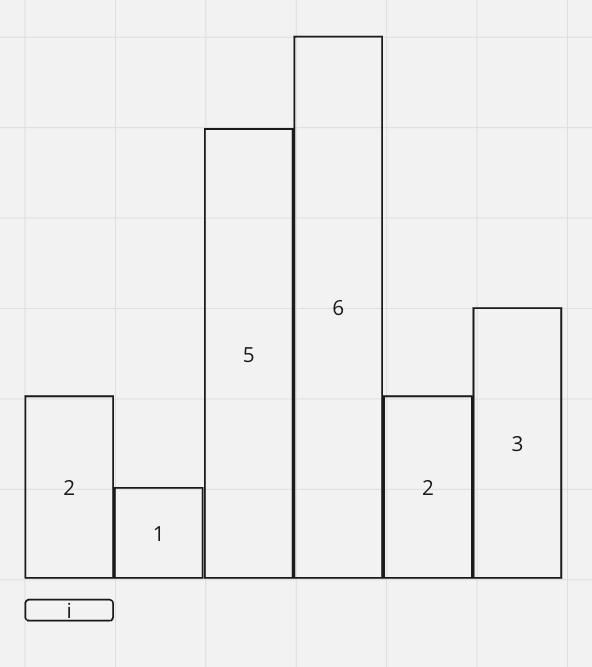
We start at i = 0 at 2. We include 2 as an increasingHistograms.

Moving on to 1, since 1 < 2 we cannot form an increasingHistograms, we have to remove 2.

When removing 2, we make sure to calculate the maxArea of 2 which is 2

As we remove 2, we also expands 1 out because of the empty space we can use

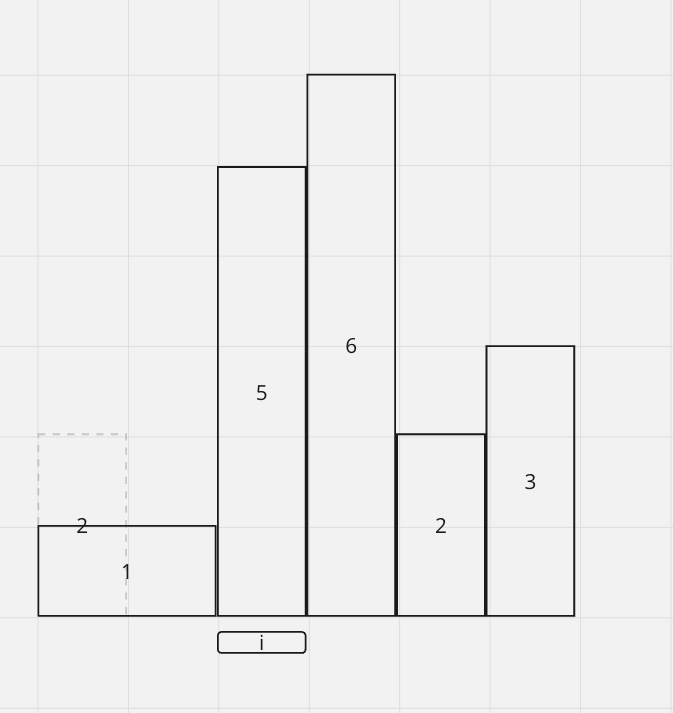
Now at 5, since 5 is an increasingHistograms we continue

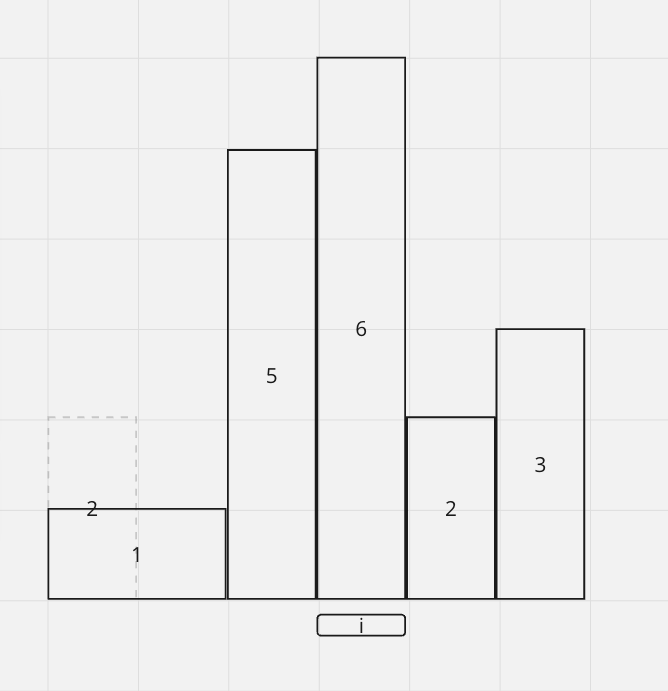
Similar to 6, it's increasing.

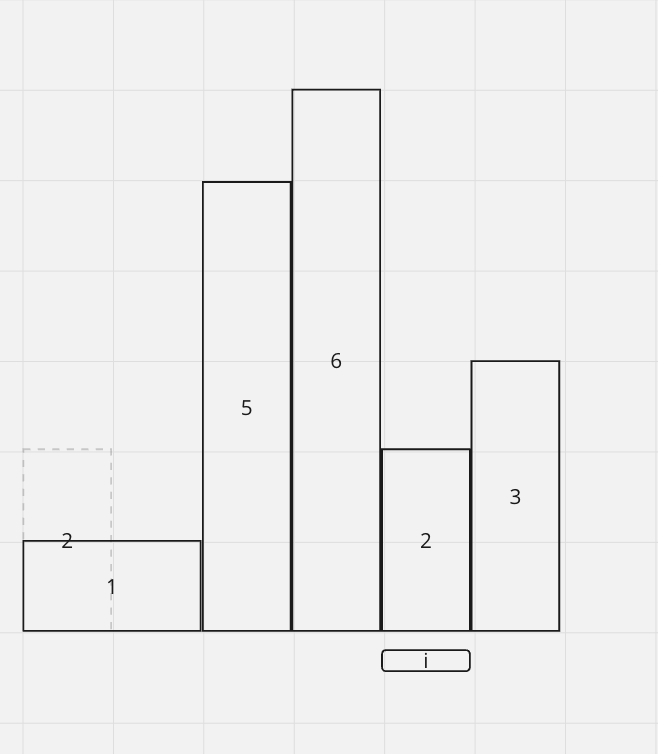
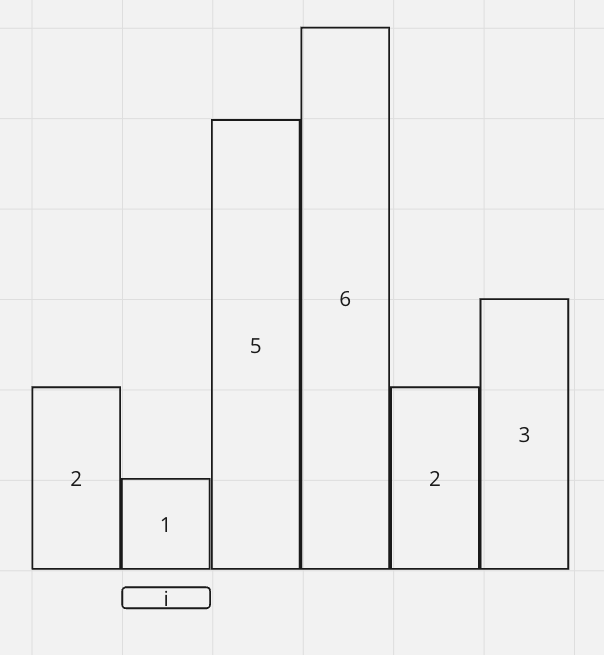
Now at 2, since 6 > 2, it's not increasing anymore. We have to pop 6 out and calculate the maxArea of 6.

So we have maxArea = 6

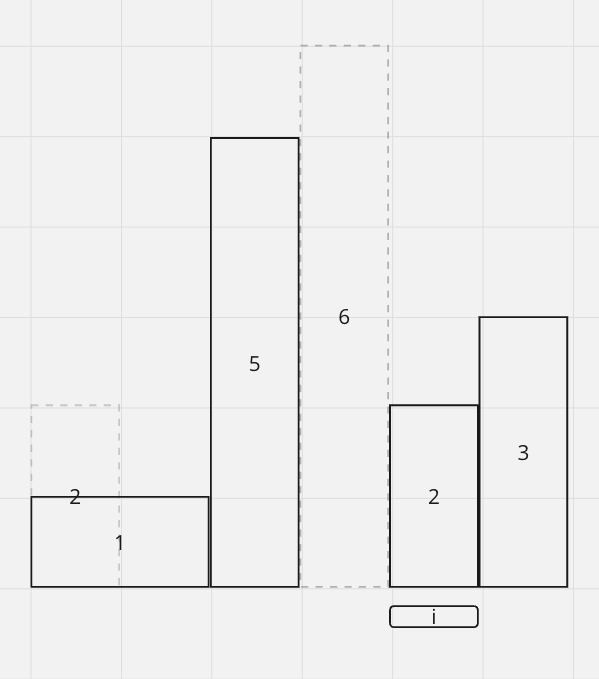
Since 5 > 2, we have to pop 5 out as well. As a result, we want to calculate the maxArea of 5. Note that from 5 we can technically expands to 2

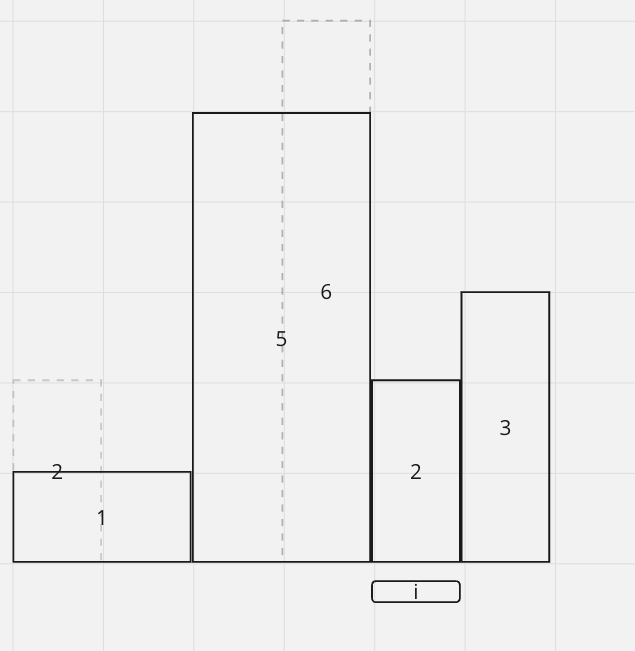
So the maxArea = 10, we pop 5 out and expand 2

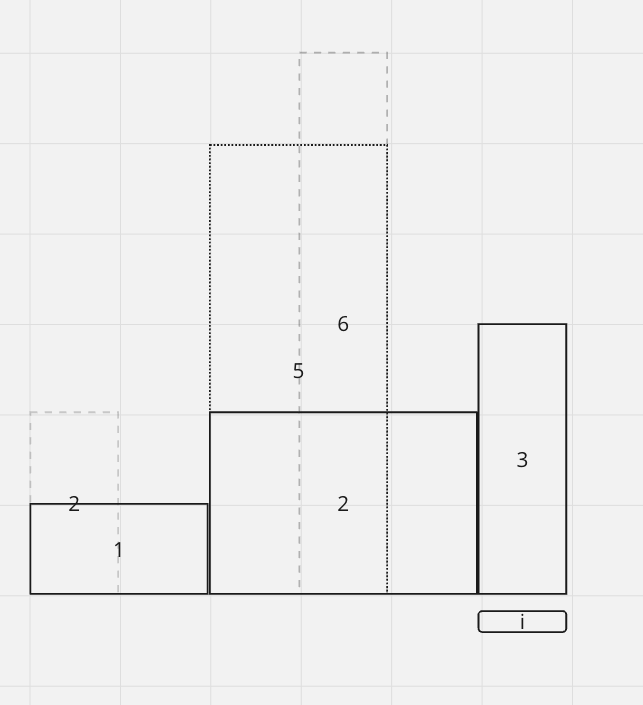
Now at 3, we can add it in our histogram that's fine.

At the end, we want to calculate the area of the above histogram manually.

Implementation

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        maxArea = 0
        increasingHistograms = []
        
        for i, height in enumerate(heights):
            startIndex = i
            
            while increasingHistograms and self.cannotFormIncreasingHistogram(increasingHistograms, height):
                topStackIndex, topStackHeight = increasingHistograms.pop()
                maxArea = max(maxArea, topStackHeight * (i - topStackIndex))
                startIndex = topStackIndex
                
            increasingHistograms.append((startIndex, height))
        
        for i, height in increasingHistograms:
            maxWidth = len(heights) - i
            maxArea = max(maxArea, height * maxWidth)
        
        
        return maxArea

    
    def cannotFormIncreasingHistogram(self, stack: List[Tuple[int, int]], height: int) -> bool:
        topStackHeight = stack[-1][1]
        return height < topStackHeight

Time complexity: $O(n)$
Space complexity: $O(n)$