Decode String

Question

Given an encoded string, return its decoded string.

The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.

You may assume that the input string is always valid; there are no extra white spaces, square brackets are well-formed, etc. Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there will not be input like 3a or 2[4].

The test cases are generated so that the length of the output will never exceed 105.

Example 1:

Input: s = "3[a]2[bc]"
Output: "aaabcbc"

Example 2:

Input: s = "3[a2[c]]"
Output: "accaccacc"

Example 3:

Input: s = "2[abc]3[cd]ef"
Output: "abcabccdcdcdef"

Solution

Why it's not a good idea to do recursion

Let's consider the following string:

3[a2[c]3[b]]

It might be tempting to do this recursively, so for example:

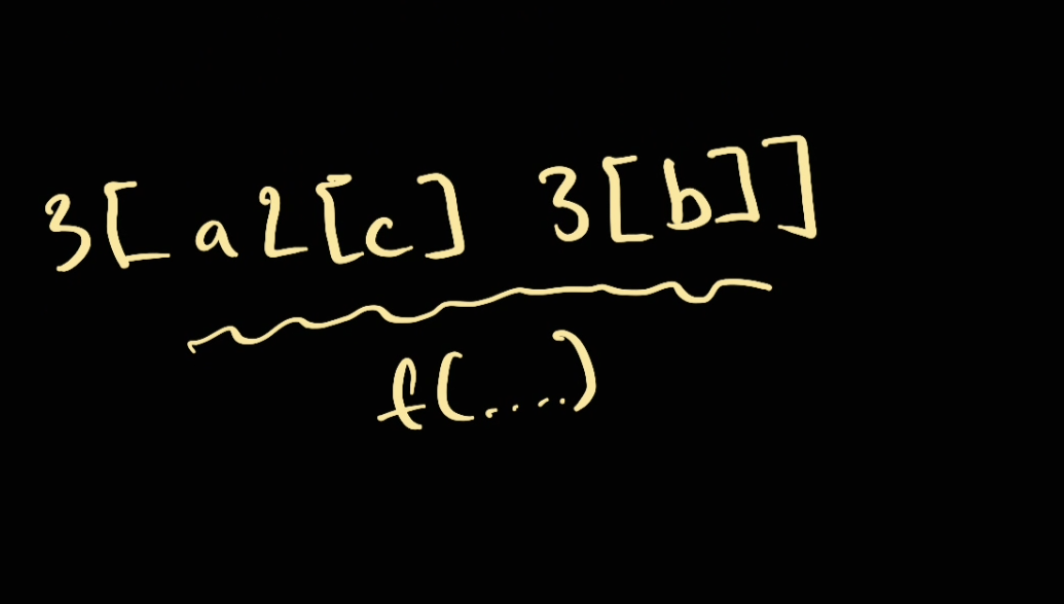
However, it's hard to know where the scope of subproblem is going to end because we're reading string by string.

So we're reading:

3[a[2c]3...?

How do we know what's $x$ of our recursion $f(x)$. The only way to know is to read through the whole string first to find the matching bracket to limit the scope of $x$.

However this will be very complex.

Intuition

If we looking at this problem, we can actually parse as the string as we go when we first encounter the ]. Let's come back to our example:

3[a2[c]3[b]]

What if we traverse the string 1 by 1:

3
3[
3[a
3[a2
3[a2[
3[a2[c
3[a2[c]

Note that in here, since we encoutered our first ], we know that we can convert the string 2[c] immediately to cc

3
3[
3[a
3[a2
3[a2[
3[a2[c
3[a2[c] -> 3[acc

Keep continue this iteration we have

3
3[
3[a
3[a2
3[a2[
3[a2[c
3[a2[c] -> 3[acc
3[a2[c]3 -> 3[acc3
3[a2[c]3[ -> 3[acc3[
3[a2[c]3[b -> 3[acc3[b
3[a2[c]3[b] -> 3[acc3[b]

Similarly in here, since we encountered ] again, we can then parse this 3[b] -> bbb:

3
3[
3[a
3[a2
3[a2[
3[a2[c
3[a2[c] -> 3[acc
3[a2[c]3 -> 3[acc3
3[a2[c]3[ -> 3[acc3[
3[a2[c]3[b -> 3[acc3[b
3[a2[c]3[b] -> 3[accbbb
3[a2[c]3[b]] -> 3[accbbb]

In here again, we encounter ]. We then convert this string 3[accbbb] -> accbbbaccbbbaccbbb

3
3[
3[a
3[a2
3[a2[
3[a2[c
3[a2[c] -> 3[acc
3[a2[c]3 -> 3[acc3
3[a2[c]3[ -> 3[acc3[
3[a2[c]3[b -> 3[acc3[b
3[a2[c]3[b] -> 3[accbbb
3[a2[c]3[b]] -> accbbbaccbbbaccbbb

Implementation

class App:
    def decodeString(self, s: str) -> str:
        stack = []

        for char in s:
            if char == "]":
                parsedSubString = self.parseSubstring(stack)
                for c in parsedSubString:
                    stack.append(c)
            else:
                stack.append(char)
        
        return "".join(stack)

    def parseSubstring(self, stack: List[str]) -> str:
        parsedSubString = "" 
        numString = "" 

        # parse string
        while stack:
            char = stack.pop()
            if char == "[":
                break
            else:
                parsedSubString = char + parsedSubString
        
        # parse integer
        while stack:
	        # Check before pop so we don't accidentally
	        # Pop out a non digit
            char = stack[-1]
            if char.isdigit():
                numString = char + numString
                stack.pop()
            else:
                break
    
        return int(numString) * parsedSubString

Time complexity: $O(n \times max(k))$

• $n$ is the length of this decode string
• $k$ is the given $k$, because we need to iteratively add $k$ length inside our stack again so it's $O(n \times max(k))$

Space complexity: $O(n \times max(k))$

• Similarly for our space, we need to store this decoded string. This is the length of the decoded string.