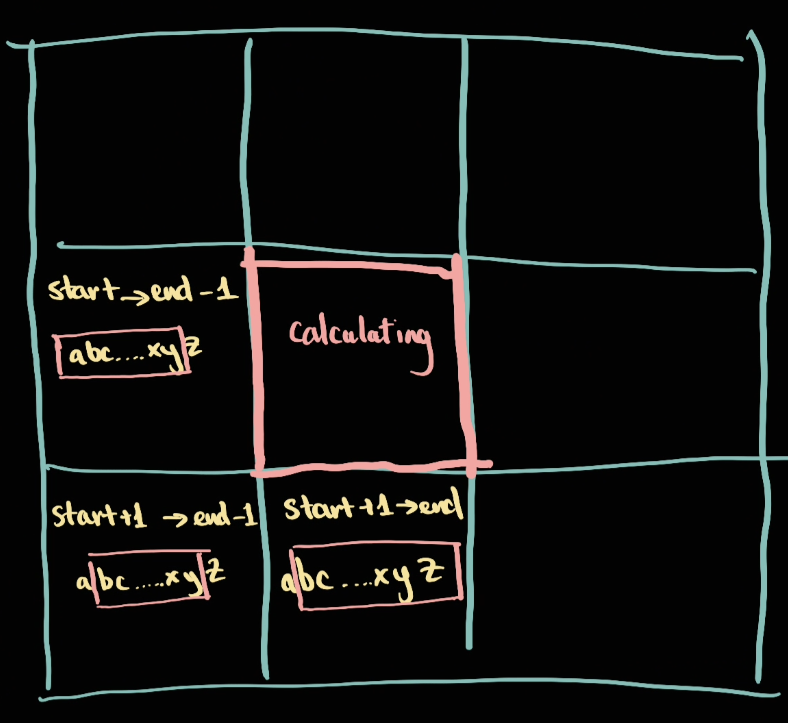
Traverse DP Table

Length traversal

A DP table normally looking like this with left handside is the start index and top is the end index

We normally traverse base on the length, for example, we can start with length = 1.

That means for each start index, we traverse up to the end index so that the distance between start index and end index == 1

Consider the following square:

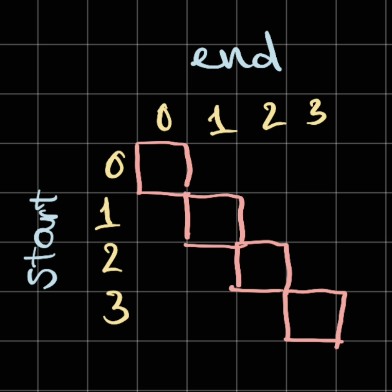
• At 0, we traverse from start = 0 and end = 0
• At 1, we traverse from start = 1 and end = 1
• At 2, we traverse from start = 2 and end = 2
• At 3, we traverse from start = 3 and end = 3

Once we done, we increase length = 2, and traverse from start again

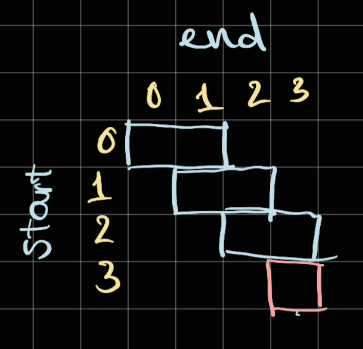
The blue rectangles are the traversal done in this iteration

We similarly do for length = 3 and length = 4

Code

def traverse(nums: List[int]):
	dp = [[0 for _ in range(len(nums))] for _ in range(len(nums))]

	for length in range(1, len(nums) + 1): # take length nums
		start = 0
		end = start + length - 1 # Inclusive end

		while (end < len(nums)):
			dp[start][end] = length
			
			start += 1
			end += 1
	return dp

traverse([0,1,2,3])

[
	[1, 2, 3, 4], 
	[0, 1, 2, 3], 
	[0, 0, 1, 2], 
	[0, 0, 0, 1]
]

Query for a result

Most of the time, we need to re-use previous result. For example, in Longest Palindrome Substring, we can query for the previous state in between start and end

It's fairly simple, for example given the following table.

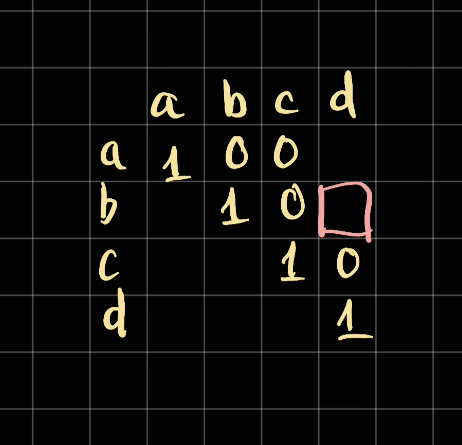
At the moment, we are considering the result of b -> d so in this case is bcd.

To calculate this result, we need to know the result in between b and d, which is c. We can take a look diagonally at start + 1 and end - 1:

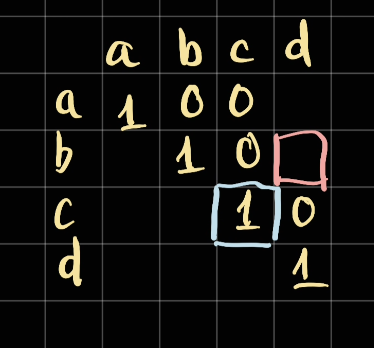
So we know that the result of c is 1

Similarly, to calculate the result of a -> d (abcd) we need the result of the inbetween (bc). We can also follow the same fomular of start + 1 and end - 1

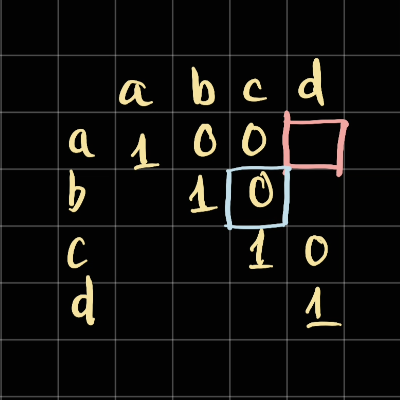
We basically have the following formula: