Longest Palindrome Substring

Question

Given a string s, return the longest palindromic substring in s.

Example 1:

Input: s = "babad"
Output: "bab"
Explanation: "aba" is also a valid answer.

Example 2

Input: s = "cbbd"
Output: "bb"

Non-DP way, check through all the possible palindrome

Revisit that to do a Palindrom check, we have 2 option:

1. Loop from outside to inside
2. Check from inside to outside

Since in here, as we're reading the string s, it's faster to do the check from inside to outside expanding from string s.

Let's go through an example

Checking from outside to inside (slower)

Let's consider this string:

mamappadaadap

If we checking from inside to outside, that means at each character we need to establish 2 pointers at the start and end of the string.

However we don't know which start and which end we can establish. Therefore, we need to do a loop. So let's imagine we're at the letter a position.

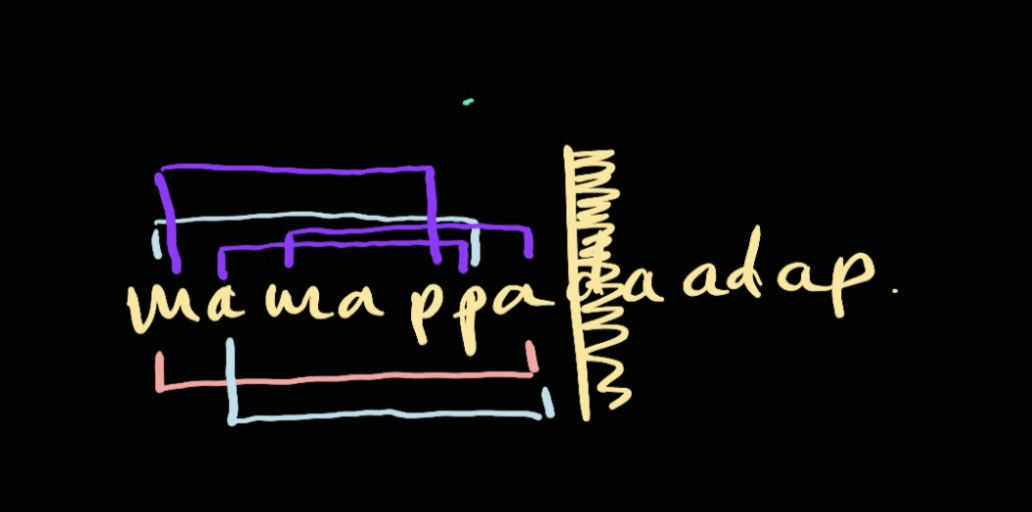
There are multiple thing we need to check here:

• Length = 7:
  • mamappa
• Length = 6
  • mamapp, amappa
• Length = 5
  • mamap, amapp, mappa
• Length = 4
  • mama, amap, mapp, appa(found)

Therefore, for each loop i, we need to check the palindrome from size of i goes down. Of course we can start from string.length to begin for optimisation. However:

• Checking for palindrom is $O(n)$ itself.
• Looping through each $n$ size is another $O(n)$
• For $n$ size we need to shift through each word of size n will be another $O(n)$

Therefore these whole thing will be $O(n^3)$

Checking inside to outside

If we checking from inside to outside, at one node we can check if it can form either:

• Odd length palindrom
• Even length palindrom

For example, given the same string mamappadaadap:

We start from m, in this case we have 1 palindrome (m)

Next, we move to a, in here we can see that we can form an odd palindrom if we expand from a:

Therefore the maximum length is now 3 (mam)

Next we move to m, also we can form ama with length 3

We then move to a, but however this one can't form any palindrom

Keep following, we can see that if we move to p, this one can form an even palindrome:

And the algorithm keeps going.

Implementation

class App:
    def longestPalindrome(self, s: str) -> str:
        if len(s) <= 1: return s
        self.longestSubstring = s[0] # Handle edge case

        for index in range(0, len(s)):
            self.findPalindromicOddString(index, s)
            self.findPalindromicEvenString(index, s)

        return self.longestSubstring


    def findPalindromicOddString(self, index: int, string: str) -> None:
        left, right = index - 1, index + 1
        self.findPalindromic(left, right, string)

    def findPalindromicEvenString(self, index: int, string: str) -> None:
        left, right = index, index + 1
        self.findPalindromic(left, right, string)
    
    def findPalindromic(self, left: int, right: int, string: str) -> None:
        while left >= 0 and right < len(string):
            if string[left] != string[right]:
                return
            
            lengthCurrentString = right - left + 1
            if lengthCurrentString > len(self.longestSubstring):
                self.longestSubstring = string[left: right + 1]
            
            left -= 1
            right += 1

Time complexity: $O(n^2)$

• $n$ times of performing $O(n)$ to perform Palindrom check
  Space complexity: $O(1)

Dynamic programming

The first thing to solve a dynamic programming problem is to determine if this is a

• 1-D Dynamic programming
• 2-D Dynamic programming

Let's first come up with an intuition of how to solve this

Intuition

We to detect if a string is a palindrom, we can consider the following:

String: babcbab

        b.....b
        ^     ^   The same, so we consider the inner group
	     
	    b.....b
	     ^   ^

As a result, we can see that if we have 2 pointers start and end. If s[start] == s[end] (the same letter), then we can check the result of F(start + 1, end - 1) (the result of the inner group).

If this result is True (inner group is a palindrome), then the new palindrome then the new palindrome would be b..innergroup..b

2-D or 1-D array

Since there are multiple inner group, for example

b.....b
   ^ ^  inner group 1
   
b.....b
 ^  ^   inner group 2

b.....b
    ^^  inner group 3

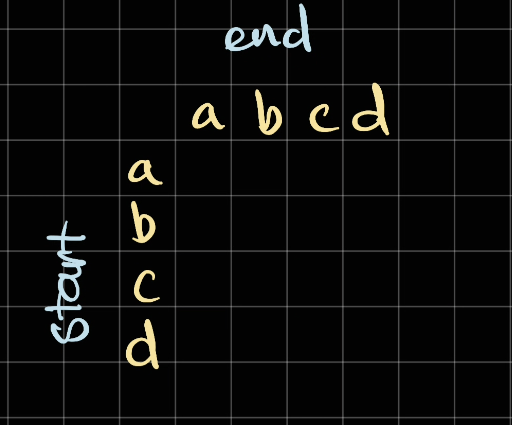
We need a 2-d array of start and end. We can represent the array as following.

Consider the example abcd. We can pick the start as the row and end as a column. The reason why we pick like this is because it's much easier to read.

For example, the following highlight

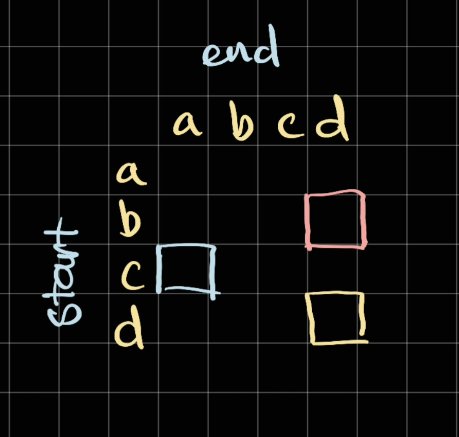
• Red squares: from b -> d (bcd)
• Blue squares: from c -> a (negative length, cannot form a string)
• Yellow square: from d -> d (d)

What to store in our table

Depends on what we store, the way we perform our algorithm changes. So far I can think of 2 ways:

1. Store the result of if the current substring is palindrome
   • As we traverse, we can keep track of the longer length (explain later on)
2. Store the longest length of palindrome up to the point
   • We need to do a backtrack in the end to find out which one has the longest palindrome.

Let's consider both option later on

How to traverse DP table

We need to traverse by length since as the length is increasing, we want to:

1. See if the current substring with given length is palindrome
2. If following method 2, we want to keep track of longest length of palindrome

For length traversal see Traverse DP Table > Length traversal

1. Store the result of if current substring is palindrome

So basically in our table, we store if the current substring is palindrome.

Consider the example abbad which we have abba is a palindrome.

Since each character itself is a palindrome, we mark that character as True

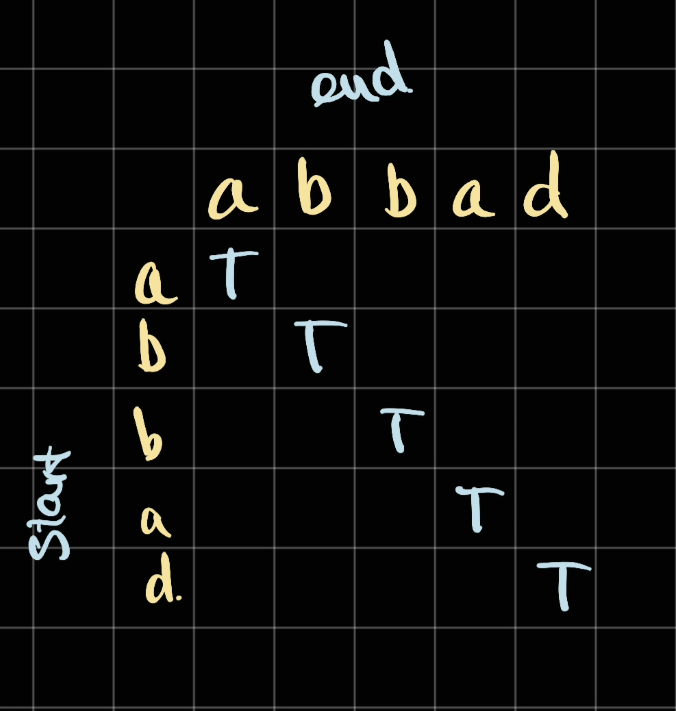
class Solution:
    def longestPalindrome(self, s: str) -> str:
        dp = [[False for _ in range(len(s))] for _ in range(len(s))]
        longestStart, longestEnd = 0, 0

        for i in range(len(s)):
            dp[i][i] = True

At 1 point of start and end we follow the following logic

• If s[start] == s[end]
  • set dp[start][end] to True in between start and end are also palindrome
  • Referring to Traverse DP Table > Query for a result, we have the condition dp[start][end] == True and dp[start + 1][end - 1] == True
• Else we set dp[start][end] to False

Edge case

Note: when filling the second row, there is an edge case.

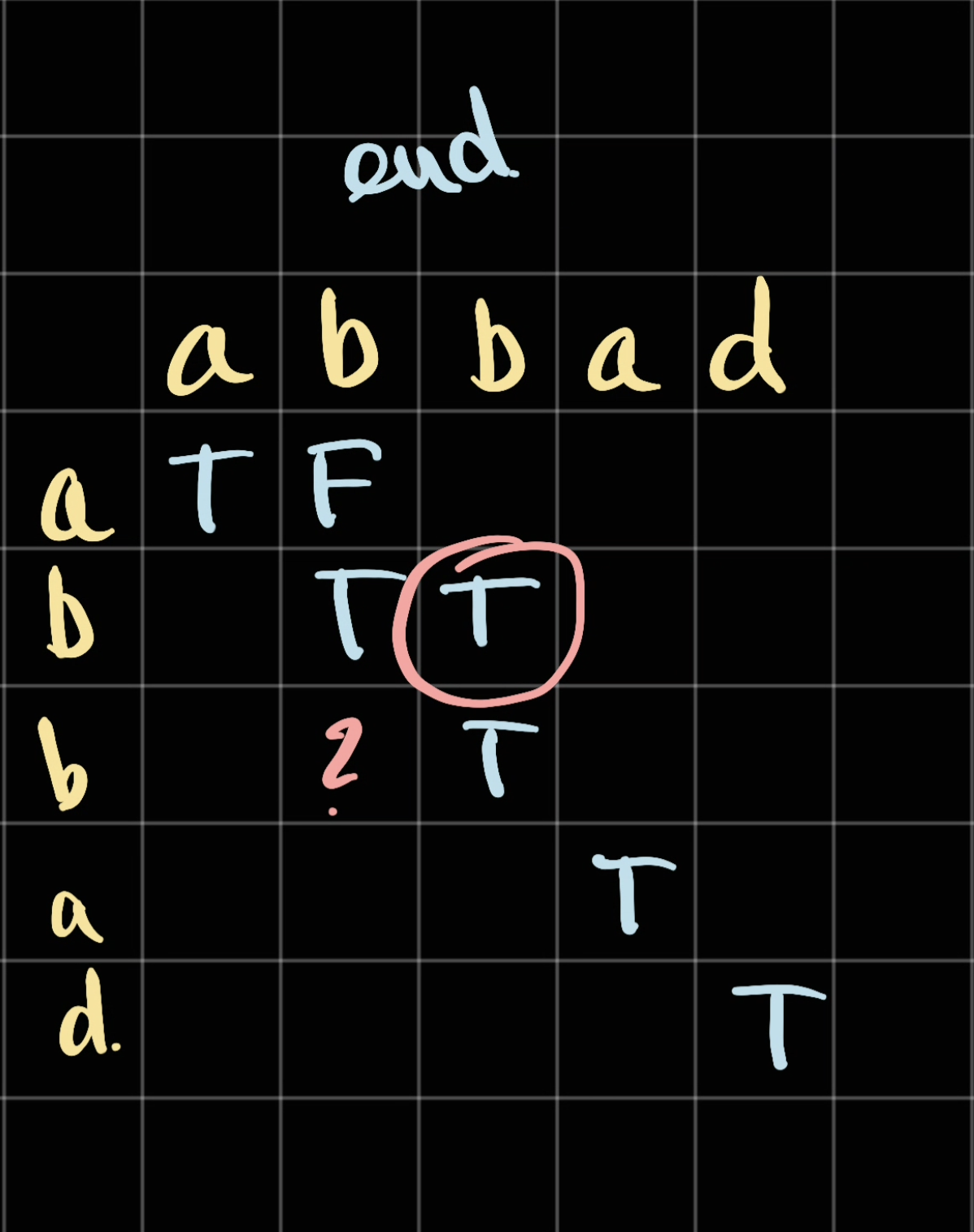
When at bb, we need to consider the inbetween b...?...b. However there is nothing inbetween, and by default we initalised our array to be all False.

So therefore in this case, we have to force a condition that if the inbetween string length < 0 then we should not consider inbetween.

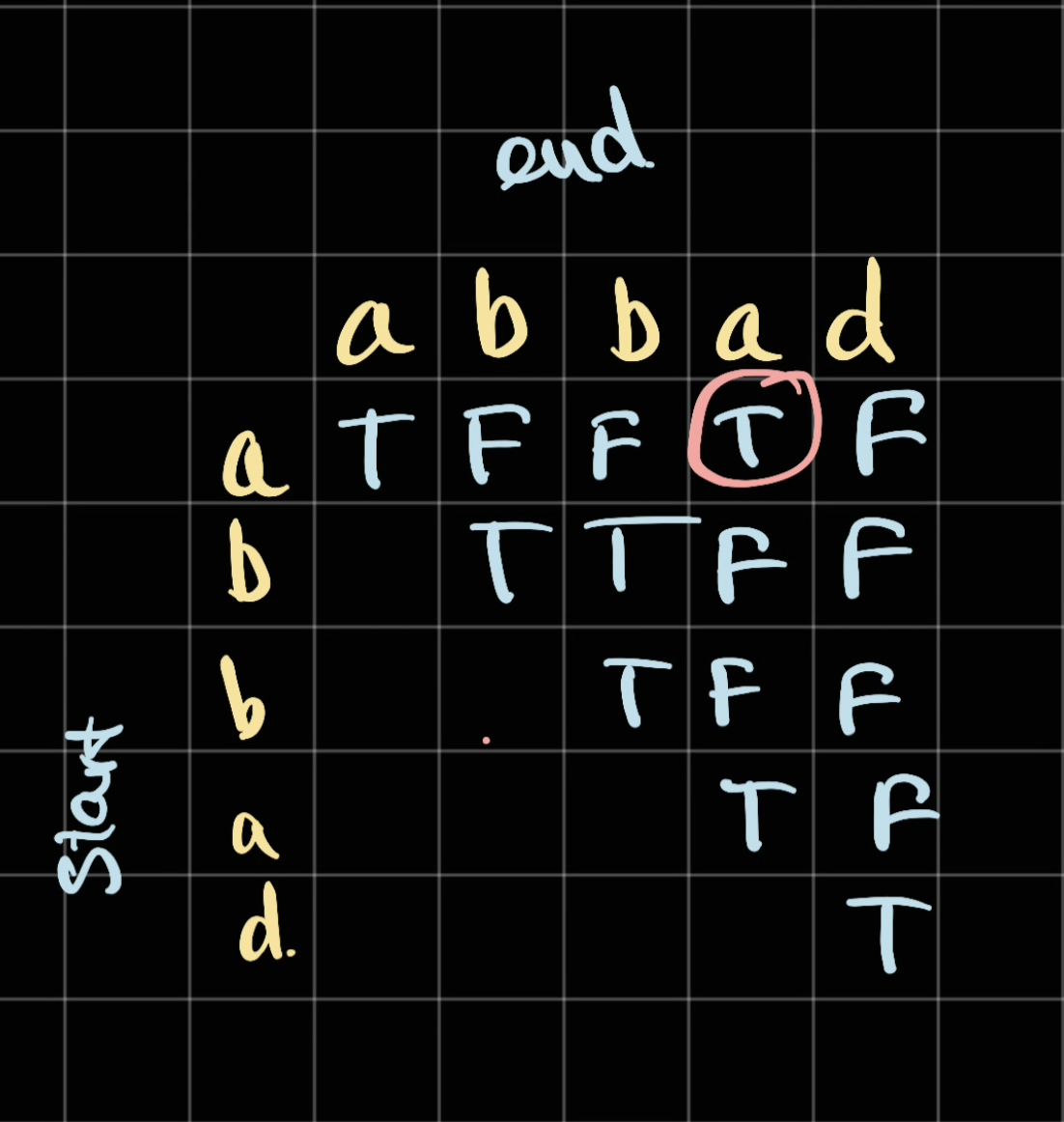
Implementation

class Solution:
    def longestPalindrome(self, s: str) -> str:
        dp = [[False for i in range(len(s))] for j in range(len(s))]

        for i in range(len(s)):
            dp[i][i] = True
        
        bestStart, bestEnd = 0, 0

        for length in range(2, len(s) + 1):
            start = 0
            end = start + length - 1

            while (end < len(s)):
                if s[start] == s[end]:
                    betweenIsPalindrome = dp[start + 1][end - 1] if end - 1 >= start + 1 else True
                    
                    if (betweenIsPalindrome) and length > (bestEnd - bestStart + 1):
                        bestStart = start
                        bestEnd = end
                    
                    dp[start][end] = betweenIsPalindrome

                
                start += 1
                end += 1
        

        return s[bestStart : bestEnd + 1]
       

Time complexity: $O(n^2)$
Space complexity: $O(n^2)$

2. Store the maximum length of palindrome so far

Similar to the above concept but we store the length of the longest palindrome substring so far

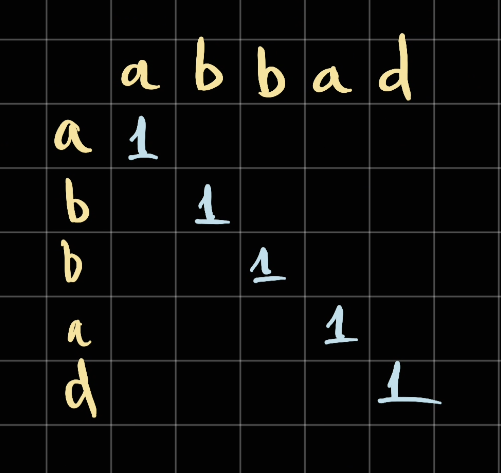
Each character is a palindrome itself so we make it 1

class App:
    def longestPalindromeSubString(self, s: str) -> int:
        dp = [[0 for _ in range(len(s))] for _ in range(len(s))] 

        for i in range(len(s)):
            dp[i][i] = 1

At 1 point of start and end we follow the following logic

• If s[start] == s[end]
  • if inbetween start and end is a palindrome, we assign dp[start][end] = dp[in_between] + 2
    • dp[in_between] = dp[start + 1][end - 1] as of Traverse DP Table > Query for a result
    • +2 because we add 2 new characters start and end
  • Else, go to the below else
• Else we need to consider all the path so far and pick the most optimal one, which we have 2 paths
  • From start to last character (end - 1)
  • Skip start: from start + 1 to current character end
  • Note: the reason why we need to either skip start or end is because since s[start] != s[end], it doesn't make sense to consider a path that has both start and end

See Traverse DP Table > Query for a result

So given the example above, we have

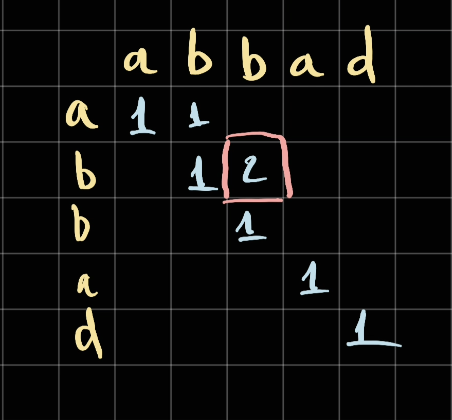
In this case, since bb is a palindrome and in between of bb is nothing. Therefore dp[bb] = 0 + 2 = 2 (we add 2 letter b and b to nothing length) .

Next we consider

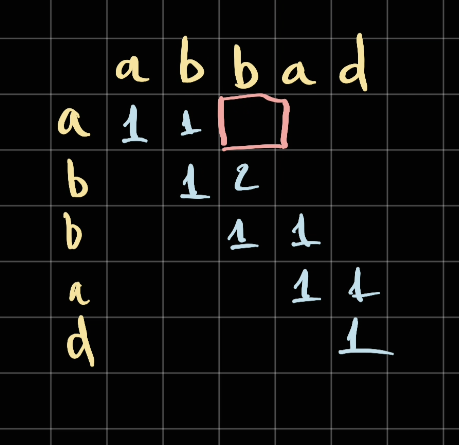
At this stage, since a != b, we should consider all the paths that doesn't have a and b together:

• ab: dp[start][end - 1]
• bb: dp[start + 1][end]

dp[start][end] = max(dp[start][end - 1], dp[start + 1][end])
dp[start][end] = max(1, 2) = 2

Which makes sense because given abb, the longest palindrome subsequences so far is 2

Similarly, in here since a == a:

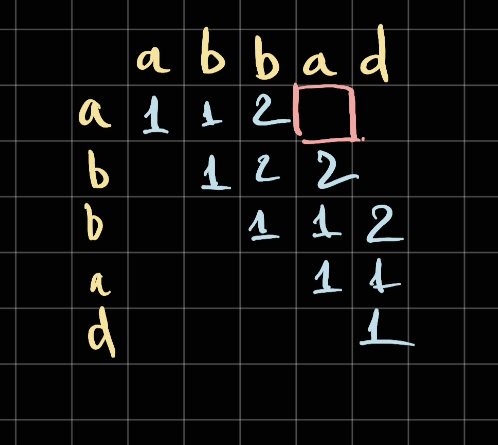
We need to take the longest substring inbetween (bb) = 2 and add 2 letter a's to the current result:

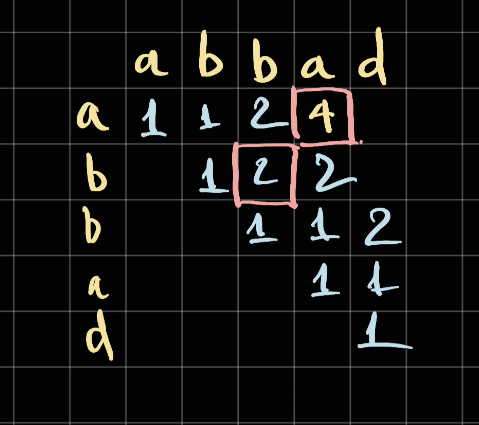
Similarly we can fill the rest

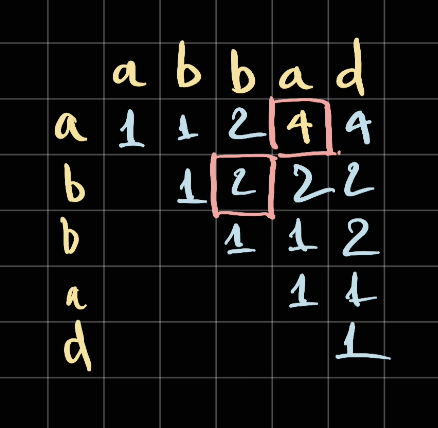
Once we have the result, we can backtrack from the 4 to find the first appearance of the 4 and get the string from start to end

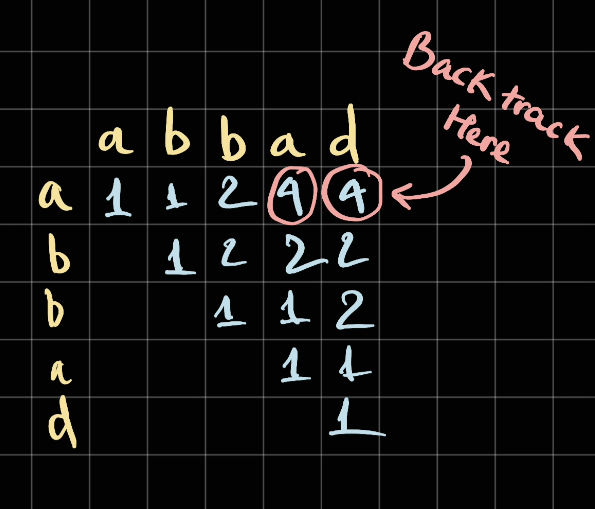
Edge case

Consider the following case of abca:

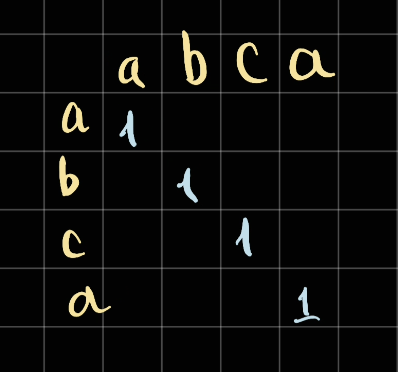
Let's pre-fill the values:

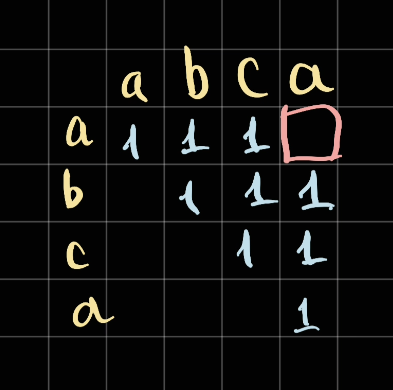
Now when filling for this square, following the same fomular, since a == a, we take the length of the substring palindrome in between bc == 1 and + 2

So we will have 1 + 2 = 3 which is not true. Because bc max palindrome length is indeed 1 but however bc is not a palindrome, so we cannot add the length on top of bc.

Therefore we need to make a rule that we only add if the length of the palindrome is the same as the length of the text in between. So in this case, we only add if length of palindrome in bc is 2 (since bc has 2 characters). However it's only 1 since it's either just b or c.

Therefore, we fall into the Else case where we take the max(dp[start][end - 1], dp[start + 1][end]) = 1

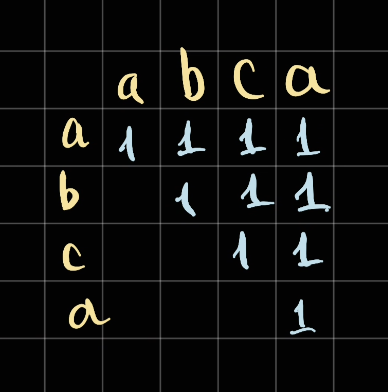
Implementation

from typing import *

class App:
    def longestPalindromeSubString(self, s: str) -> int:
        dp = [[0 for _ in range(len(s))] for _ in range(len(s))] 

        for i in range(len(s)):
            dp[i][i] = 1

        for length in range(2, len(s) + 1):
            start = 0
            end = start + length - 1 # inclusive

            while (end < len(s)):
                if s[start] == s[end]:
                    lengthPreviousSubstring = (end - 1 - (start + 1)) + 1

                    if dp[start + 1][end - 1] == lengthPreviousSubstring:
                        # previous substring must be palindrome
                        dp[start][end] = dp[start + 1][end - 1] + 2 # 2 is 2 new characters
                    else:
                        dp[start][end] = max(
                            dp[start + 1][end], # star + 1 -> end group
                            dp[start][end - 1] # start -> previous char group
                        )
                else:
                    dp[start][end] = max(
                        dp[start + 1][end], # star + 1 -> end group
                        dp[start][end - 1] # start -> previous char group
                    )

                start += 1
                end += 1
        
        return self.getResult(dp, s)

    
    def getResult(self, dp: List[List[int]], s: str):
        start, end =  0, len(dp) - 1
        currMax = dp[start][end]
        nextValue = currMax

        while True:
            if end > 0 and dp[start][end - 1] == currMax:
                end -= 1
            elif start < len(dp) - 1 and dp[start + 1][end] == currMax:
                start += 1
            else:
                break
        
        return s[start: end + 1]

Time complexity: $O(n^2) + O(n^2)$

• Actual DP: $O(n^2)$
• Backtrack for result: $O(n^2)$

Space complexity: $O(n^2)$