Longest Common Subsequence

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

• For example, "ace" is a subsequence of "abcde".

A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Intuition

To find the longest common subsequence, we align the 2 words as a table, for example, consider the 2 word "abcdef" and "dcef" — in which the longest subsequence should be cef (3 length)

We can start by marking on the row to the col. Considering the row is what we have so far:

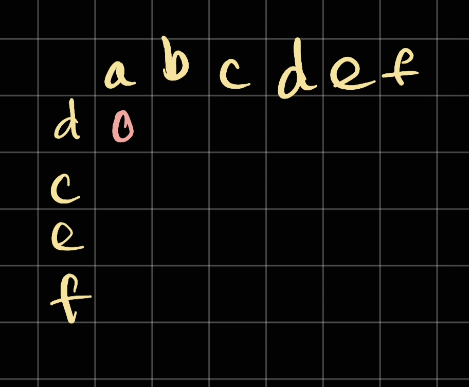
So in this case, we compare d with a. Since they're different, we mark that as 0 as the length of subsequence:

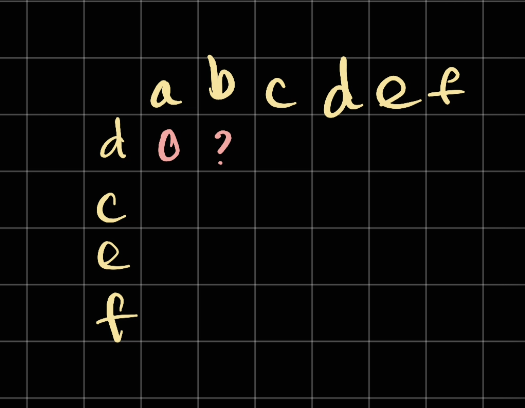
Next, we consider d with b, since they're also different, we mark it as 0.

The length of the longest subsquence when comparing d and ab is 0 which makes sense.

Similarly, we do the same for c.

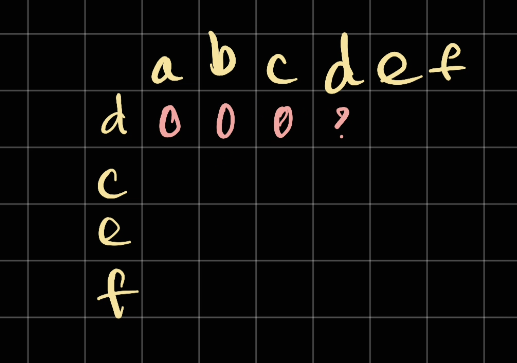
Now in here, since d is the same as d, which means the longest common subsequence of d vs abcd is 1. So we mark it as 1

At e, since d != e, but the longest common subsequence so far is 1 so we mark the longest common subsequence of d vs abcde is 1.

Similarly, in f it's also 1

Now come back to c, this is essentially comparing dc vs a. Since c != a, we try to see what the result of d vs a. (Since we always want to record the best value before the conflict c != a happens, which in this case is d vs a — before considering c)

Since at d vs a, it's 0, we take the result as 0.

Similarly in here, we're comparing dc with ab. Since c != b, we try to take the result before c != b. Which are dc vs a and d vs ab, both of these are 0, therefore it's 0:

Now in here we're comparing dc with abc. Now since c == c. We want to take (the result of d vs ab) + 1 Because we want to find the best result before c == c in the string dc vs abc so it should be d vs ab

Since dp[d vs ab] = 0, we make this 0 + 1 = 1

Now in here, we're comparing dc vs abcd, since c != d. We need to record the max value before c != d happens:

• at d vs abcd we have 1.
• at dc vs abc we have 1.

Therefore we can have max(1, 1) = 1

Similarly, at e we can take the max(dc vs abcd, d vs abcde) which give us 1

Continuing the same logic so far:

If stringA[row] != stringB[col]: 
	take max(dp[left], dp[top])

If stringA[row] == stringB[col]: 
	take dp[row - 1, col - 1] + 1
	     ^^^^^^^^^^^^^^^^^^^^
	     previous max previous subsequence 

We have this table filled:

So the maximum subsequence is 3

Implementation

class App:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        self.maxLength = 0
        
        dp = [[0 for _ in range(len(text1))] for _ in range(len(text2))]

        for row in range(len(text2)):
            for col in range(len(text1)):
                if(text2[row] == text1[col]):
                    dp[row][col] = self.calculateLength(dp, row, col)
                else:
                    dp[row][col] = self.getLength(dp, row, col)
                self.maxLength = max(self.maxLength, dp[row][col])

        return self.maxLength

    def calculateLength(self, dp, row, col):
        previousResult = dp[row - 1][col - 1] if row >= 1 and col >= 1 else 0
        return previousResult + 1

    def getLength(self, dp, row, col):
        topResult = dp[row - 1][col] if row >= 0 else 0
        leftResult = dp[row][col - 1] if row >= 0 else 0

        return max(leftResult, topResult)

Time complexity: $O(m \times n)$

• $m$ and $n$ is length of text1 and text2
  Space complexity: $O(m \times n)$
• $m$ and $n$ is length of text1 and text2