Skip List

Definition

Skip list is a probabilistic datastructure where it's created base on a sorted link list.

The datastructure looks like below:

This is a sorted linked list, sorted from the left -> right.

In here the bottom level $S_0$ it's a sorted linked list, with the list node defined as below:

class ListNode:
	above: Optional[ListNode]
	left: Optional[ListNode]
	right: Optional[ListNode]
	below: Optional[ListNode]
	val: int

The above level ($S_1$, $S_2$, … $S_5$) are called express lane. Which is created base on a probability.

So for example, everytime at a node, we going to flip a coin with chance of $\frac{1}{2}$ probability. If it's head, we're going to copy that node to the above level, if it's tail, we do nothing.

Search

When searching for a node, we search from the top-left node of the skip list:

We basically go down first and then go right.

So in this case, for example if we need to search for node 0.

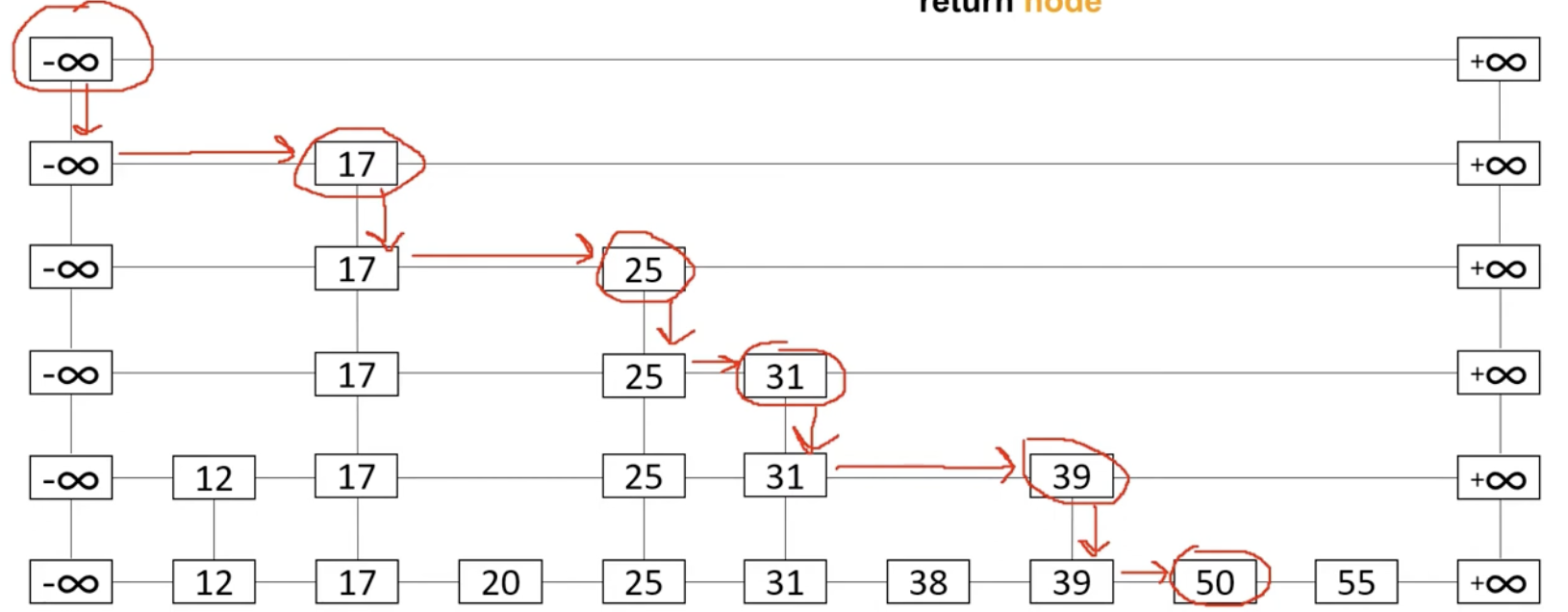
In here, since we cannot drop down anymore, we've found the node.

Pseudo code

search(n):
	node = start

	while node.getBelow() != null
		# Go down
		node = node.getBelow()
		
		while node.getNext().getVal() <= n:
			# Go right
			node = node.getNext()

	return node

Time complexity: $O(logn)$ — since we keep dropping down the tree

What if the key doesn't exist

For example if we're searching for 49, the following will happen:

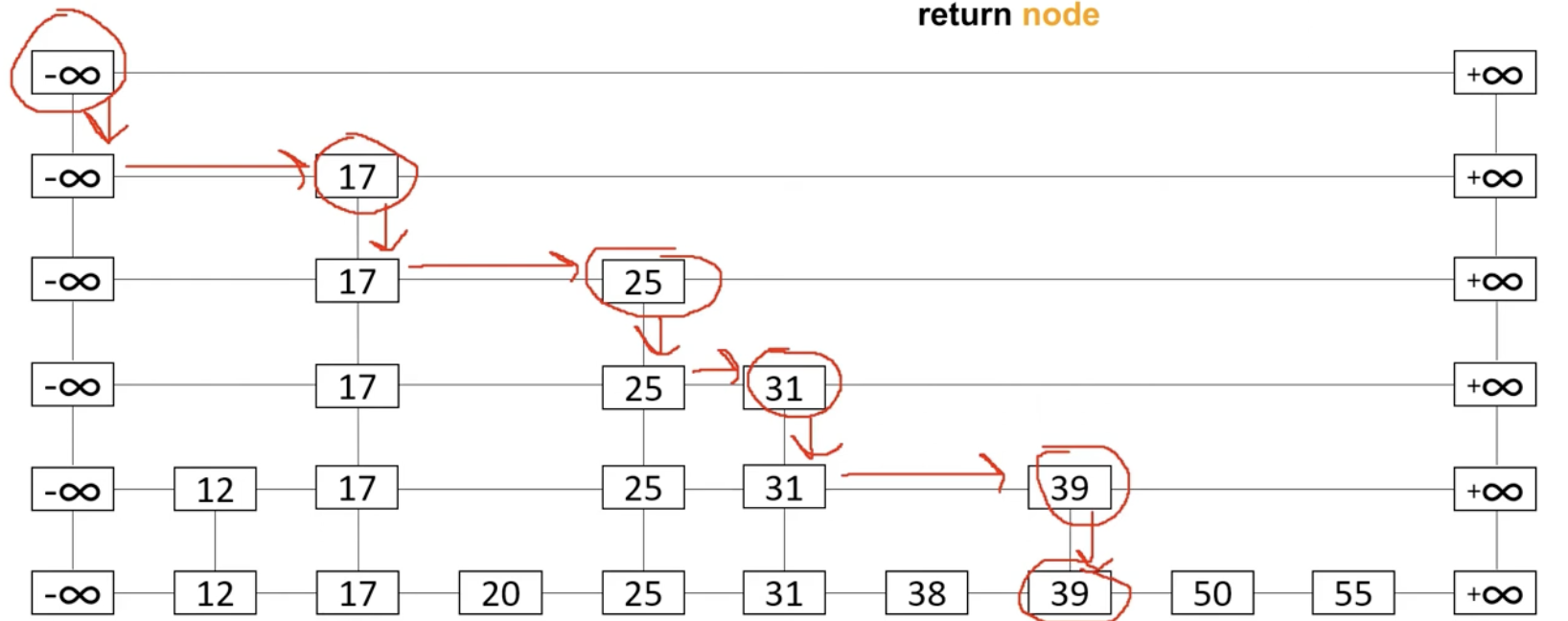
Base on the algorithm, it will return 39 because we're finding the largest node <= 49

Which key would we return if there are multiple key

For example if we're searching for 17 which appears multiple time in the second column

In this case, we will return the bottom level node

Insertion

We need to search for the key first.

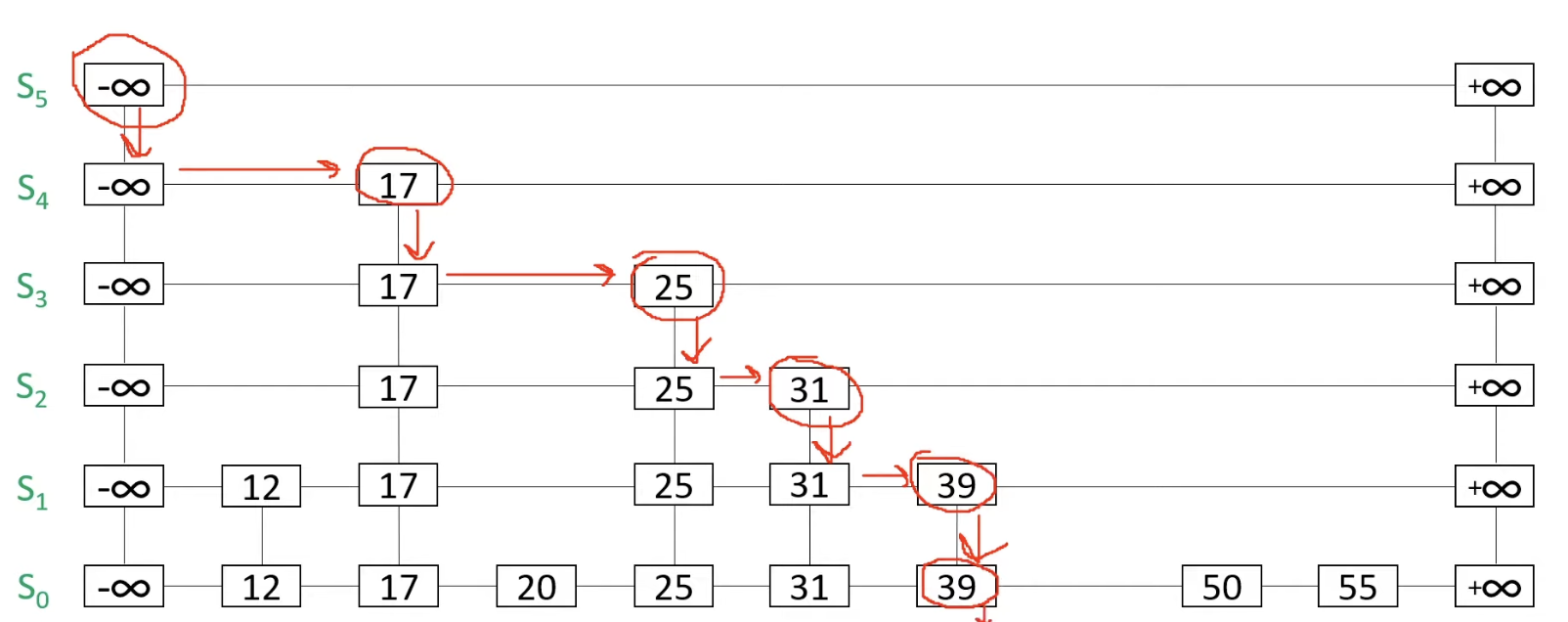
For example, in this case, we will add the node 42. That means we need to search for something <= 42

In this case, we can perform the above search operation. As a result, we obtained 39 at the bottom level.

As a result, we can add 42 in between 39 and 50.

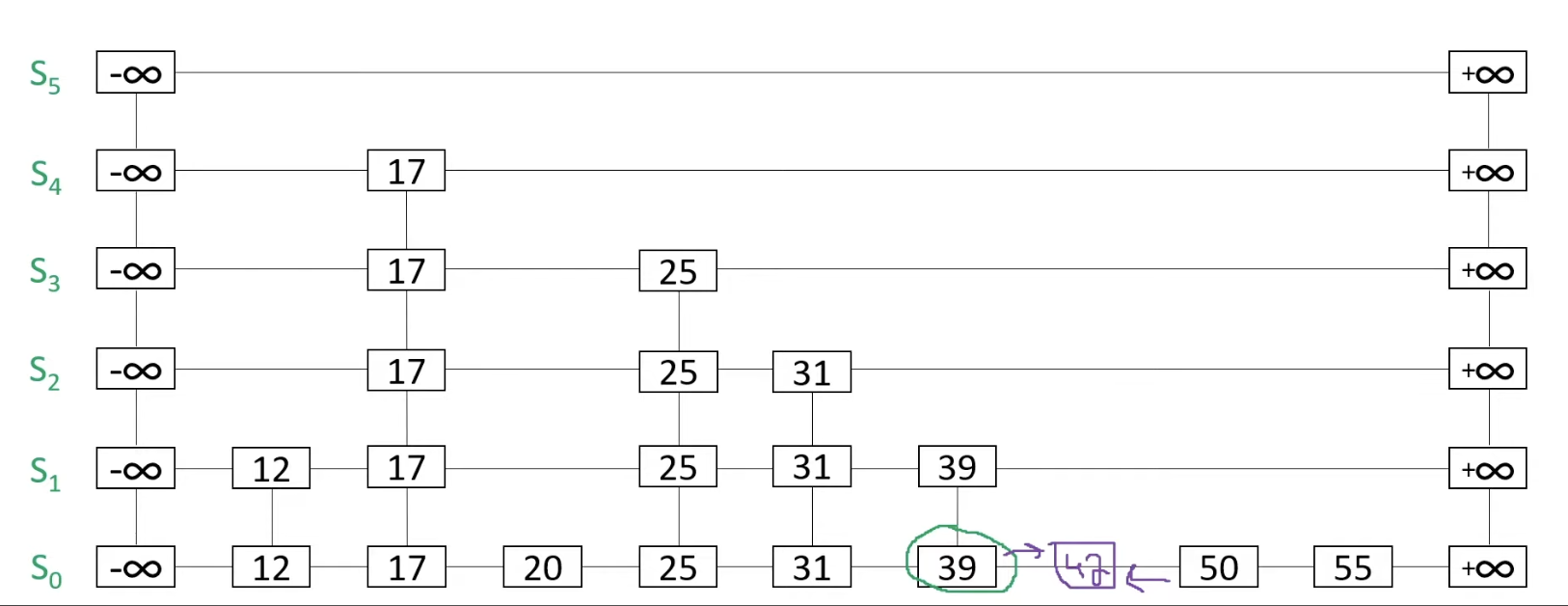
Now we're going to flip the coin, if it's head, we're going to add a node to the above row, if it's tail, we do nothing.

For example, we flipped the coin and it's head. As a result, we will add 42 in the above row:

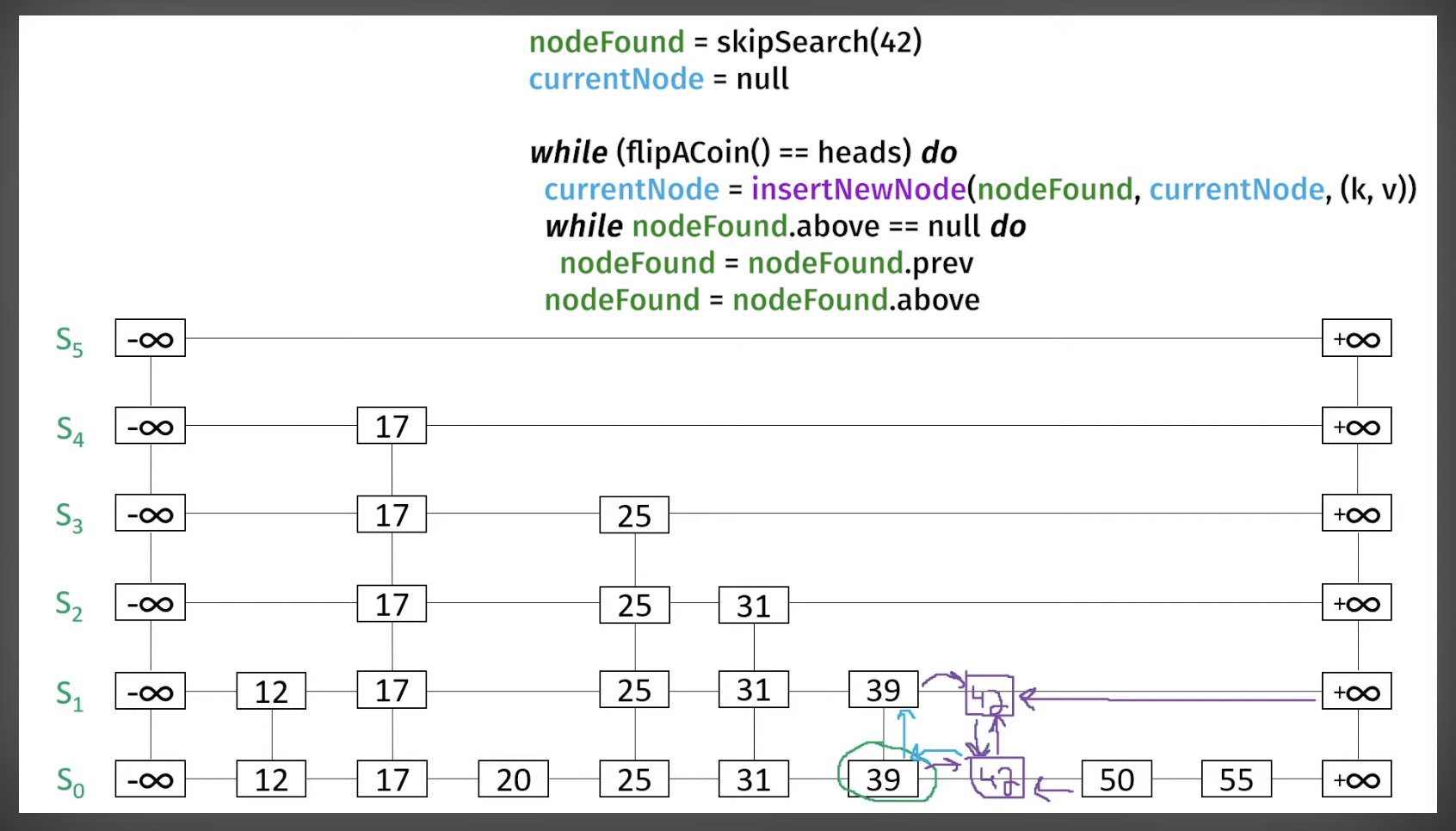
So we:

• Assign S_0.42.above = new ListNode(42)
• Assign S_1.42.below = S_0.42
• Find previous node of S_0.4 that has above: (39)
  • Assign S_1.39.next = S_1.42
  • Assign S_1.42.previous = S_1.39

Similarly, if we roll the dice again and get head, we insert 42 in the above. So we go below

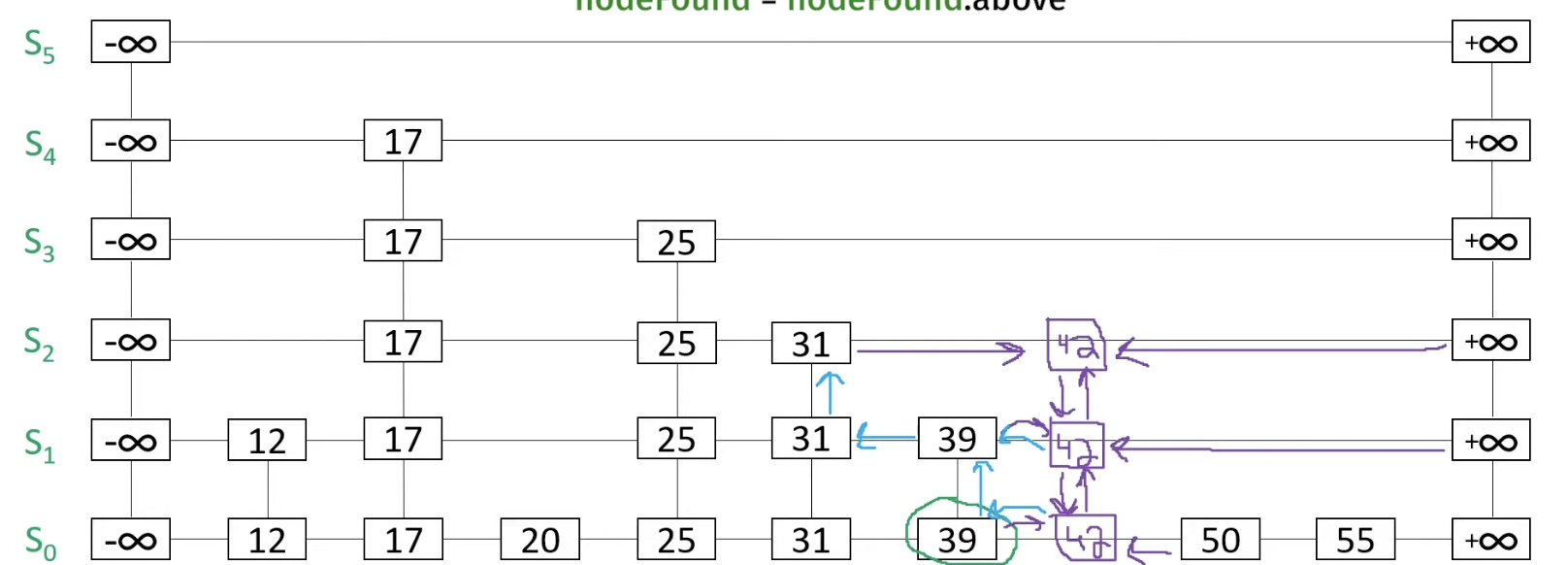
So at S_2.42, we go down to S_1.42 and then find the previous node that has above (S_1.31). We then connect S_2.31 to S_2.42.

Next, if we flip the coin, and it's tail, we stop the operation.

Pseudocode

nodeFound = search(42)

while (flipCoin() == heads) do
	nodeFound.next = ListNode(42)

	# If doesn't have the above node
	while nodeFound.above == null do:
		nodeFound = nodeFound.prev
	nodeFound = nodeFound.above

Time complexity: $O(logn)$

Deletion

Let say we want to delete 25

We also use the search operation to 25. If it doesn't exist (the return node is not 25 then we return null)

So after searching for 25, we have:

In here since the node is indeed 25, we can delete.

In here we going to map 20 -> 31 and 31 -> 20 (bypassing 25)

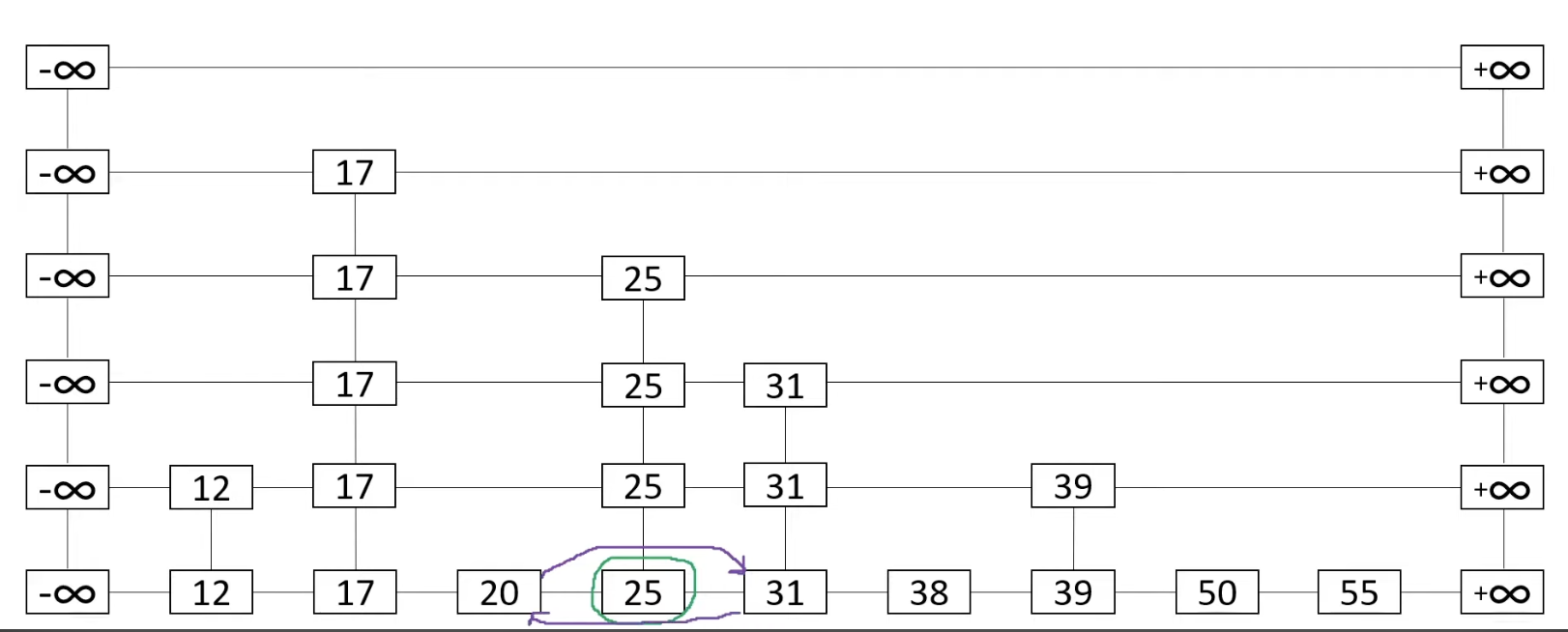
After that, we go upper level and do the same thing: 17 -> 31, 31 -> 17

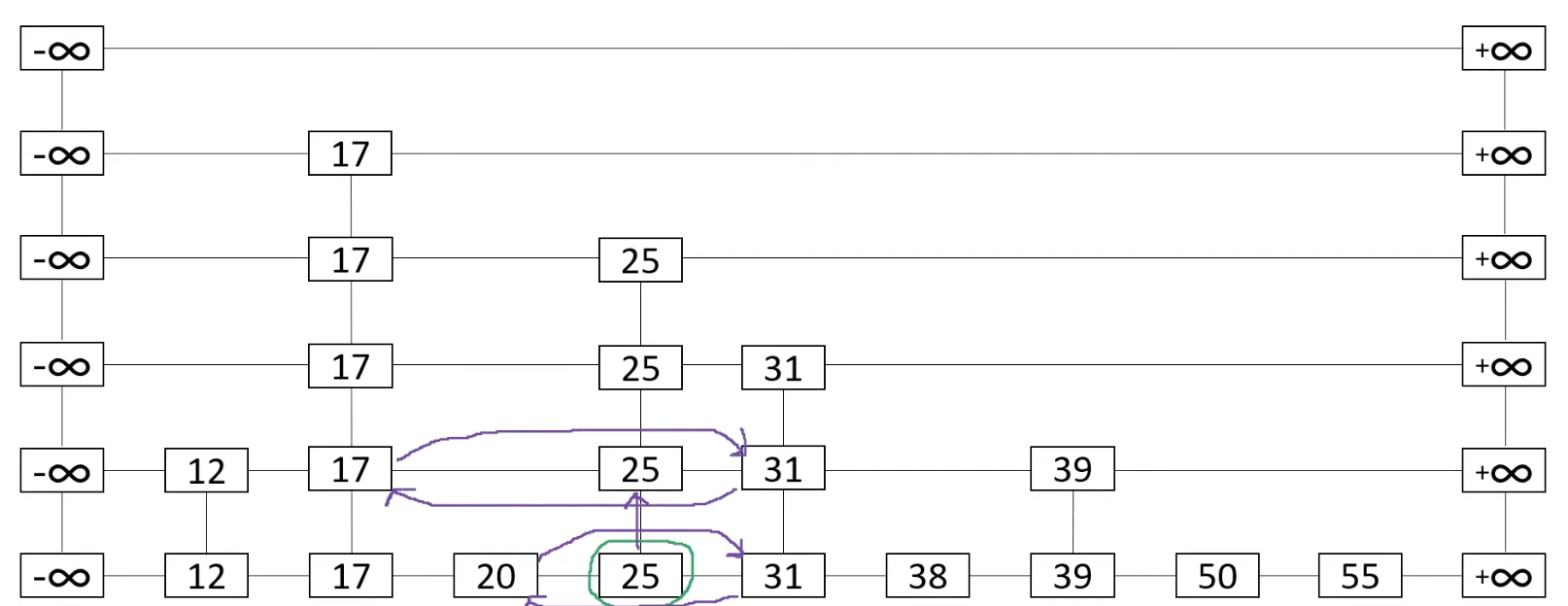
We continue to go up again and do the same thing

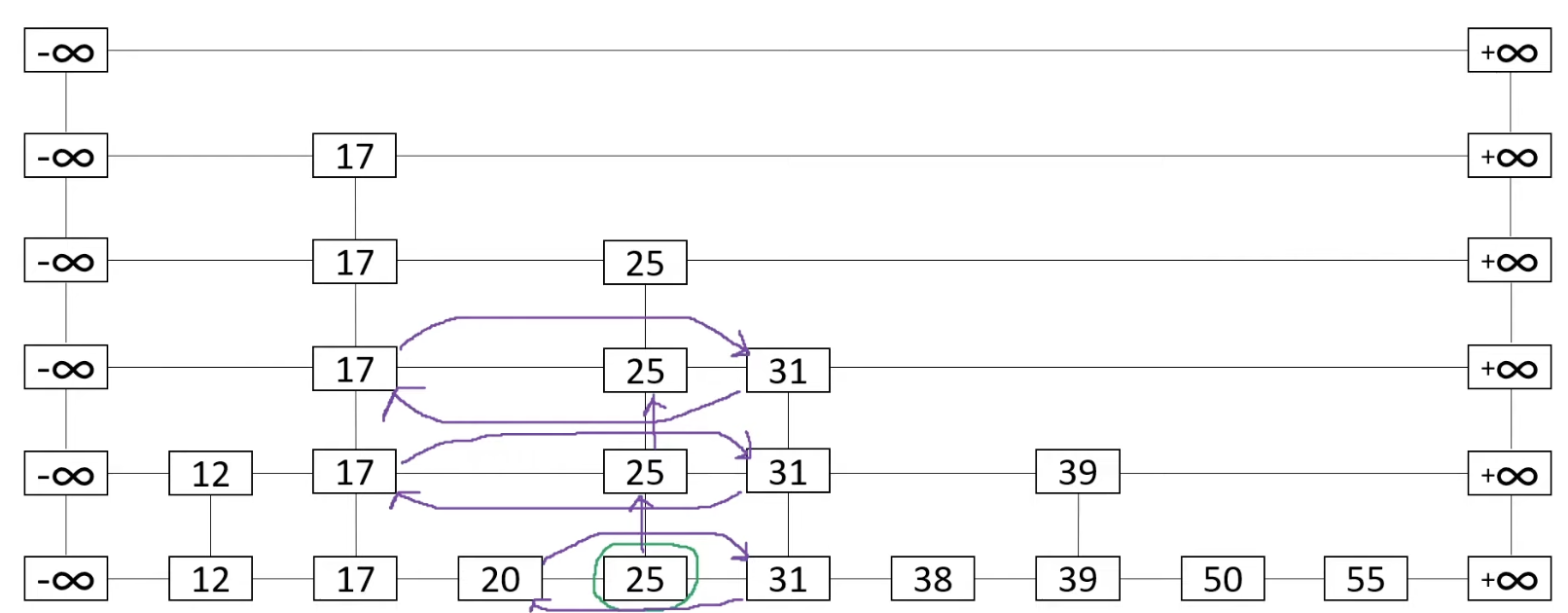
And go up again

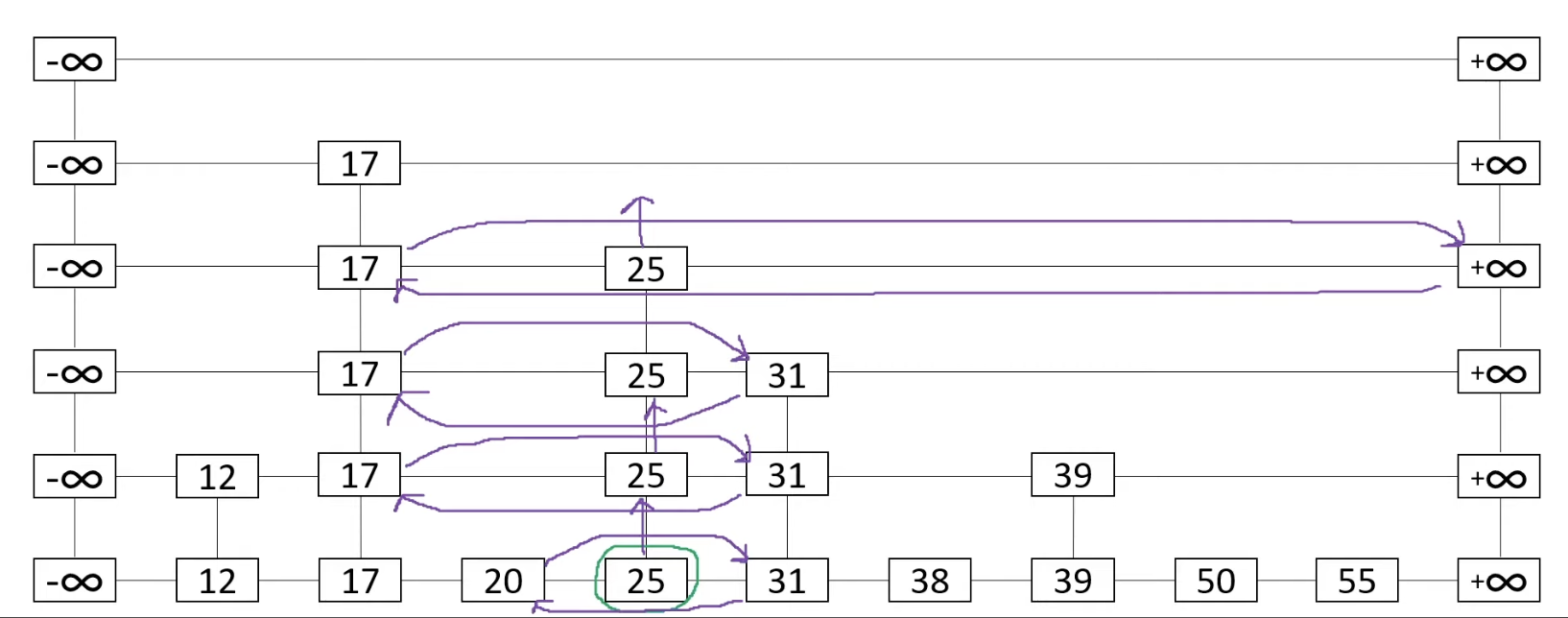
Since 25 has no above node, we stop

Pseudo code

nodeFound = search(25)

if nodeFound.val != 25: stop

while (nodeFound != null) do
	nodeFound.prev <-> nodeFound.next
 
	# If doesn't have the above node
	nodeFound = nodeFound.above

Time complexity: $O(logn)$ — since we're traversing through the height of the tree.