WordSearch II

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1

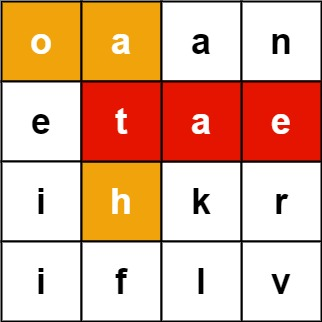
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2

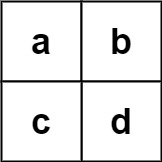
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Solution

This question focusing on how to use a Trie and search recursively within a Trie.

Intuition

Considering the following example:

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]]
words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

To solve this problem

1. We can start building a Trie of each word
2. We can start doing graph traversal dfs at each cell of the board and check if we can form any words from our Trie.

Gotcha

In here, for example if we have

Let ssay our given word is

eaabcdfga

The DFS will traverse as the following direction:

1. Visit e — since we have e as the root in our Trie

2. visit a — since our a is the next candidate in our Trie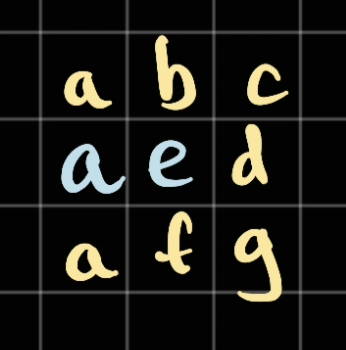
   Note: in here we mark the blue one visited

3. Now we have to visit another a, let's assume it chose the one below.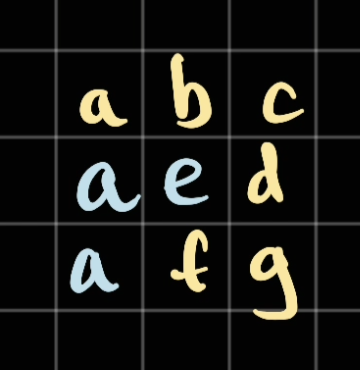

4. Here we look for the next character which is b, however there is no b here. As a result, we will go to the top one:
   

5. Fast forward, we go to visit ...bcdfga, let's mark this path as the red colour:
   

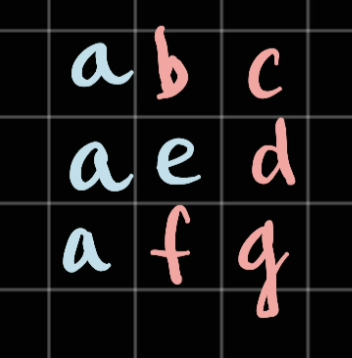
6. As we can see, we cannot see the last a since the letter is already visited. Therefore, we will need to pop out the visited a if we can't process further.

Implementation

from collections import defaultdict
from dataclasses import dataclass
from typing import *
import unittest

@dataclass
class TrieNode:
    value: int
    neighbours: Dict[str, 'TrieNode']
    isWord: bool
    numberOfCharacters: int

    def __init__(self, value):
        self.value = value
        self.neighbours = {}  # " { a : TrieNode(a) }"
        self.isWord = False
        self.numberOfCharacters = 0

    def insertWord(self, word: str) -> None:
        currNode = self
        for char in word:
            if char not in currNode.neighbours:
                currNode.neighbours[char] = TrieNode(char)
            
            currNode = currNode.neighbours[char]
            currNode.numberOfCharacters += 1

        currNode.isWord = True
    
    def pruneTree(self, word):
        # Pruning the tree once we finished searching for a word to reduce time for next word
        currNode = self
        for letter in word:
            currNode = currNode.neighbours[letter]
            currNode.numberOfCharacters -= 1
            

class App:
    def __init__(self):
        self.result = None

    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        root = TrieNode("*")
        self.root = root

        for word in words:
            root.insertWord(word)
        
        self.result = []
        
        for row in range(len(board)):
            for col in range(len(board[0])):
                if board[row][col] in root.neighbours:
                    self.searchWord(board, row, col, root, [], "")

        return self.result

    def searchWord(self, board, row, col, node, visited, word):
        if not self.withinBoundary(board, row, col, visited):
            return

        letter = board[row][col]
        if letter not in node.neighbours: return

        currNode = node.neighbours[letter]
        if currNode.numberOfCharacters == 0: return
        
        visited.append((row, col))

        word += letter

        if currNode.isWord:
            self.result.append(word)
            currNode.isWord = False # avoid duplication
            self.root.pruneTree(word)

        for dr, dc in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
            self.searchWord(board, row + dr, col + dc, currNode, visited, word)

        visited.pop()


    def withinBoundary(self, board, row, col, visited):
        return not (row < 0 or col < 0 or col >= len(board[0]) or row >= len(board) or (row, col) in visited)

Time complexity: $O(n \times L + rows \times cols \times 4^L)$

• We have $n$ is the length of the
• $L$ is the length of the longest word
• $4^L$ is because for each row, col, we need to search 4 direction.

Note:

• At the end of the node we need to do a visited.pop() to release the node out for the next use, because potientially we need to reuse this letter
• When we find the node, we mark the node isWord = False so that we don't readding it to the result anymore next time we found it.
• We're adding pruneTree here, which means to reduce the number of nodes in the Trie so that next time it search quicker.