Design Add And Search Words DataStructure

Question

Design a data structure that supports adding new words and finding if a string matches any previously added string.

Implement the WordDictionary class:

• WordDictionary() Initializes the object.
• void addWord(word) Adds word to the data structure, it can be matched later.
• bool search(word) Returns true if there is any string in the data structure that matches word or false otherwise. word may contain dots '.' where dots can be matched with any letter.

Example

Input
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
Output
[null,null,null,null,false,true,true,true]

Explanation
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True

Solution

Note that in here it's not regular Implement Trie Prefix Tree question since we have the dot. The dot can be matches with any of the letter, which means we have to do a horizontal search.

For example, if we have these words:

abcde
abcxf
abd
abcj

And we're searching for abc.f.

When we're at the c in abc. We need to decide which branch to go:

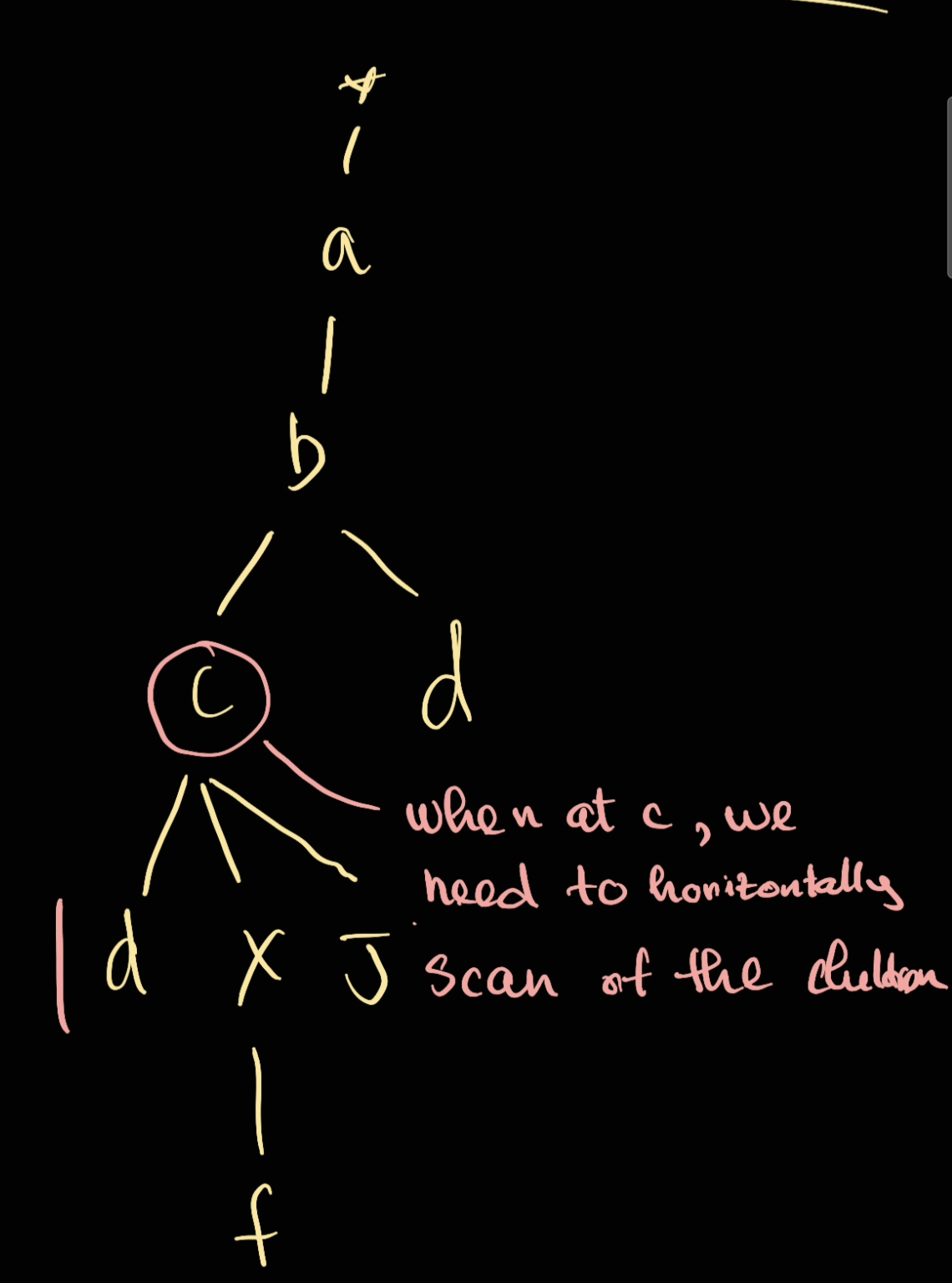
Therefore it needs to be a recursion. Which will be done at the parent level

So we will:

1. At parent level, we check if it has the next letter we're looking for or . (wildcard) :
   • if it's . (wildcard):
     • We perform step 1 for all the children of the current parent. So essentially skipping to check that child
   • else:
     • If yes (it has next letter we looking for) then we perform the same thing for the next letter. So now parrent = nextLetter
     • If No then we return False
2. When the parent is the leaf (we've finished traversing through all the letter in our search space).
   • At this point, the parent should be the last character of our search word. We can simply return parent.isWord

Implementation

from typing import *
import unittest

class Node:
    value: str
    children: Dict[str, 'Node']
    isWord: bool
    def __init__(self, value: str) -> None:
        self.value = value
        self.children: Dict[str, 'Node'] = {} # { 'a': Node('a') }
        self.isWord = False
        
class App:
    def __init__(self):
        self.root = Node(None)
        self.wildCard = "."
        pass

	# Regular Trie add word
    def addWord(self, word: str) -> None:
        if len(word) < 1: raise Exception("Invalid input")
        
        currentNode = self.root
        
        for letter in word:
            if not letter.isalpha():
                raise Exception("Invalid input")
            
            if letter not in currentNode.children:
                currentNode.children[letter] = Node(letter)

            currentNode = currentNode.children[letter]
        
        currentNode.isWord = True


    def search(self, word: str) -> bool:
        if len(word) < 1: raise Exception("Invalid input")
        return self.searchFromNode(self.root, 0, word)

    def searchFromNode(self, parentNode: 'Node', letterIndex: int, word: str) -> bool:
        if letterIndex >= len(word): return parentNode.isWord
        
        currentLetter = word[letterIndex]

        if currentLetter != self.wildCard and not currentLetter.isalpha():
            raise Exception("Invalid input")

        if self.parentNodeDoesNotHaveLetter(parentNode, currentLetter):
            return False
        
        if currentLetter == self.wildCard:
            for letter in parentNode.children:
                if (self.searchFromNode(parentNode.children[letter], letterIndex + 1, word)):
                    return True
            return False

        return self.searchFromNode(parentNode.children[currentLetter], letterIndex + 1, word)

    def parentNodeDoesNotHaveLetter(self, node: str, letter: str) -> bool:
        return letter != self.wildCard and letter not in node.children

Time complexity:

• addWord: $O(n)$ where $n$ is the length of the word being added
• searchWord: $O(m)$ where $m$ is the sum of all the words length in our tries
  • This is because worst case we need to go search for every single path

Space complexity: $O(m)$ where $m$ is the sum of all the words in our tries.

• This is because the tries can expand in 2 dimensions, we needs to calculate when it's expanding side-way