Validate Binary Search Tree

Question

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

**Example 1

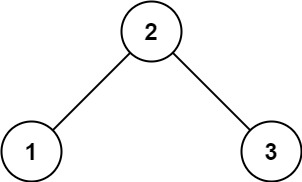
Input: root = [2,1,3]
Output: true

Example 2

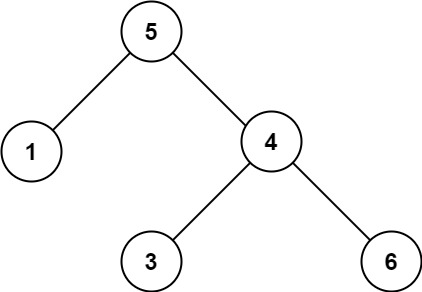
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Solution

For this question, it's important to see the boundary of the node, for example node E in here will be within the range of (B, A).

As a result we need to keep track of a min, max for each node.

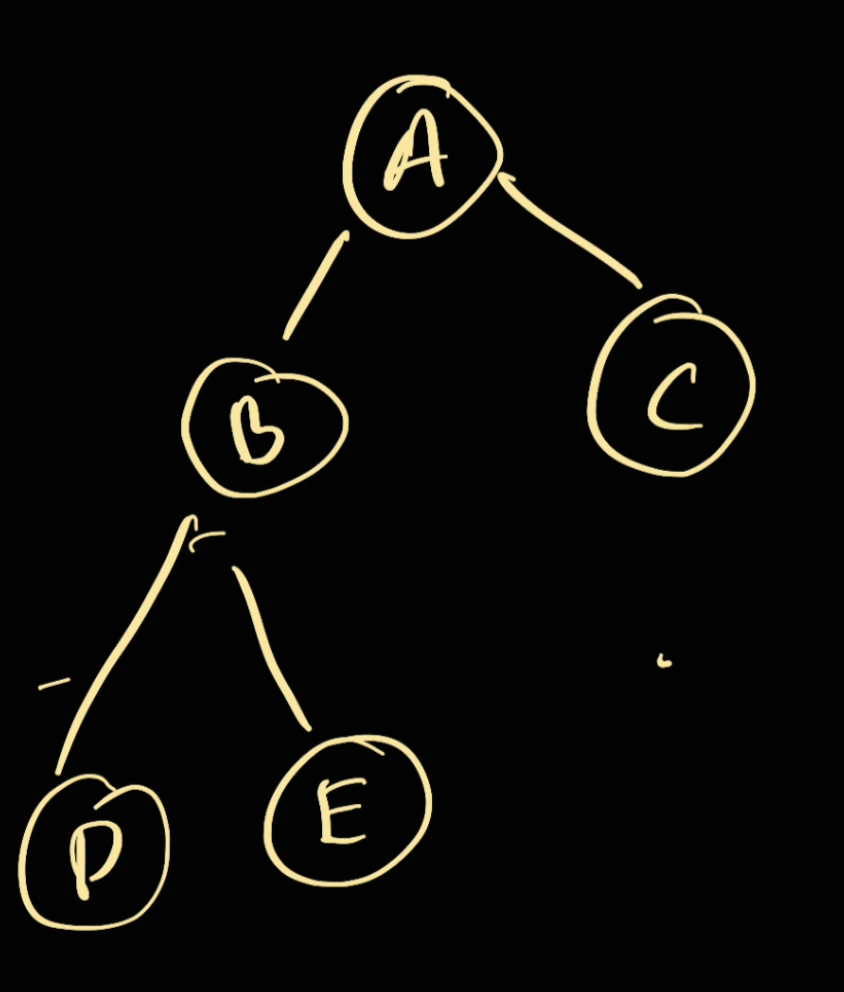
We can have this following rules:

• If we go right node, we set the min = currentNode
• If we go left node, we set the max = currentNode

Implementation

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        if not root: raise Exception("Illegal arguments")
        return self.isSubTreeValid(root.left, float('-inf'), root.val) and self.isSubTreeValid(root.right, root.val, float('inf'))

    def isSubTreeValid(self, node: 'TreeNode', minValue: int, maxValue: int) -> bool:
        if not node: return True
        if node.val <= minValue or node.val >= maxValue: return False
        return self.isSubTreeValid(node.left, minValue, node.val) and self.isSubTreeValid(node.right, node.val, maxValue) 

Time complexity: $O(n)$ — given that $n$ is the number of nodes
Space complexity: $O(logn)$ — recursion space is depth of the tree so $logn$