Find Minimum In Rotated Sorted Array

Question

You are given an array of length n which was originally sorted in ascending order. It has now been rotated between 1 and n times. For example, the array nums = [1,2,3,4,5,6] might become:

• [3,4,5,6,1,2] if it was rotated 4 times.
• [1,2,3,4,5,6] if it was rotated 6 times.

Notice that rotating the array 4 times moves the last four elements of the array to the beginning. Rotating the array 6 times produces the original array.

Assuming all elements in the rotated sorted array nums are unique, return the minimum element of this array.

A solution that runs in O(n) time is trivial, can you write an algorithm that runs in O(log n) time?

Example 1:

Input: nums = [3,4,5,6,1,2]

Output: 1

Example 2:

Input: nums = [4,5,0,1,2,3]

Output: 0

Example 3:

Input: nums = [4,5,6,7]

Output: 4

Constraints:

• 1 <= nums.length <= 1000
• -1000 <= nums[i] <= 1000

Solution

For this question, the hard thing is to find what we are looking for in binary search.

Ideally, we want to go to the part that has smaller value.

[!important]
This one is different than Binary Search In Rotated Sorted Array because we are not looking for a particular value.

We're just looking for which side is smaller. So we always go to that side. In Binary Search In Rotated Sorted Array we would need to consider more scenario

Now we have 3 possible scenarios

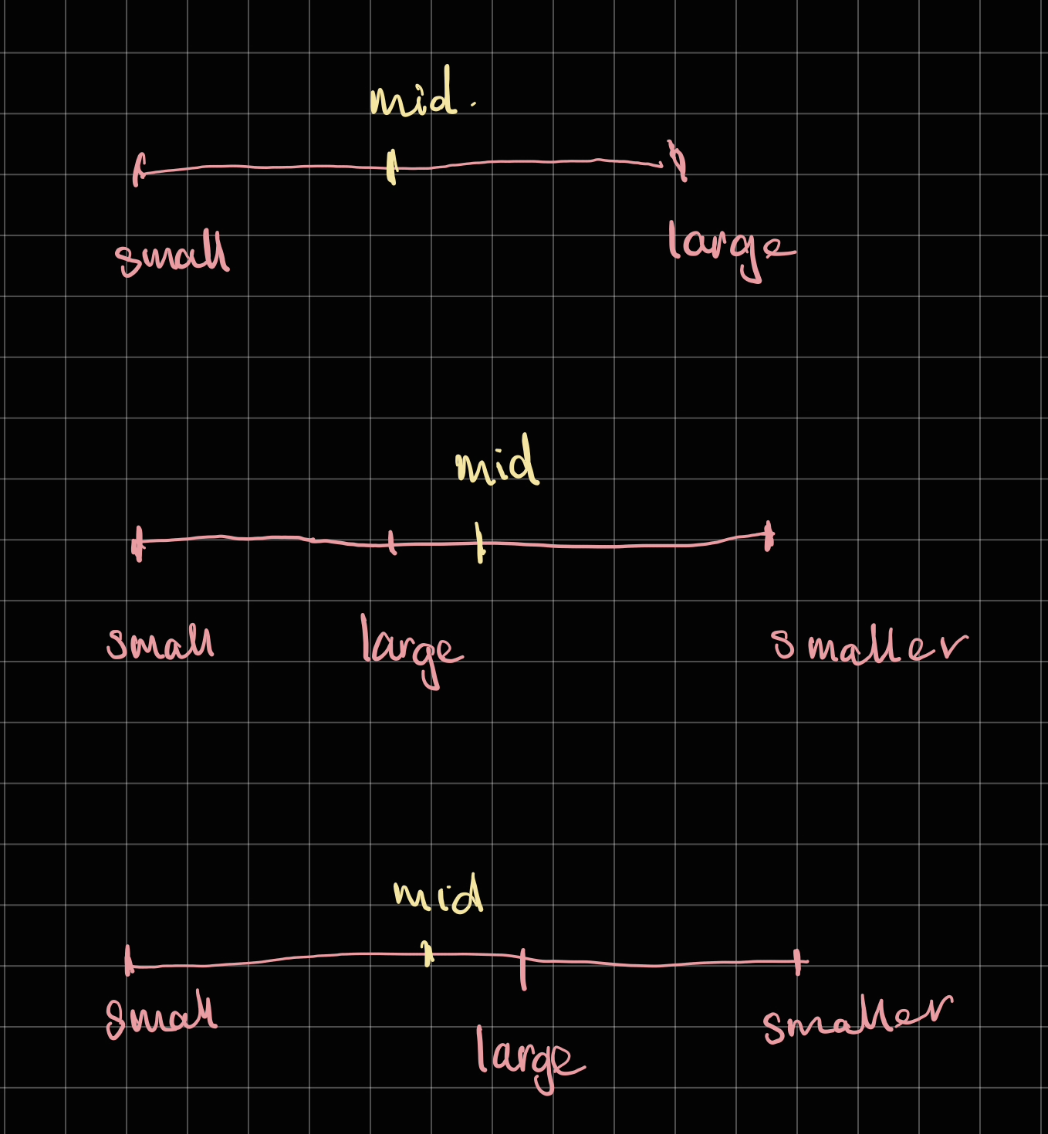
In this case, we basically want to search in the smaller part.

Note that in the case of rotation, because of the nature of this question, if the array is rotated that means the right side numbers are always smaller than the left.

• We shouldn't think like this as we're comparing against mid. Smaller or not needs to compare against mid instead of left or right.
• Normally left is smaller than mid, in that case we should traverse left. Now in the case that right is smaller than mid we then need to traverse right

Therefore, we have the formular:

If right is smaller than mid, search on the right

This is also true for this case here:

     mid
      v
6,7,1,2,3,4,5

Since 5 is not smaller than mid, so the smaller side 
should be on the right.

Solution

class App:
    def findMin(self, nums: List[int]) -> int:
        left = 0; right = len(nums) - 1
        
        while left < right:
            mid = (left + right) // 2

            if nums[right] < nums[mid]:
                # Go right
                left = mid + 1
            else:
                # Go left
                right = mid
        
        return nums[left]

Time complexity: $O(logn)$
Space complexity: $O(1)$