Binary Search

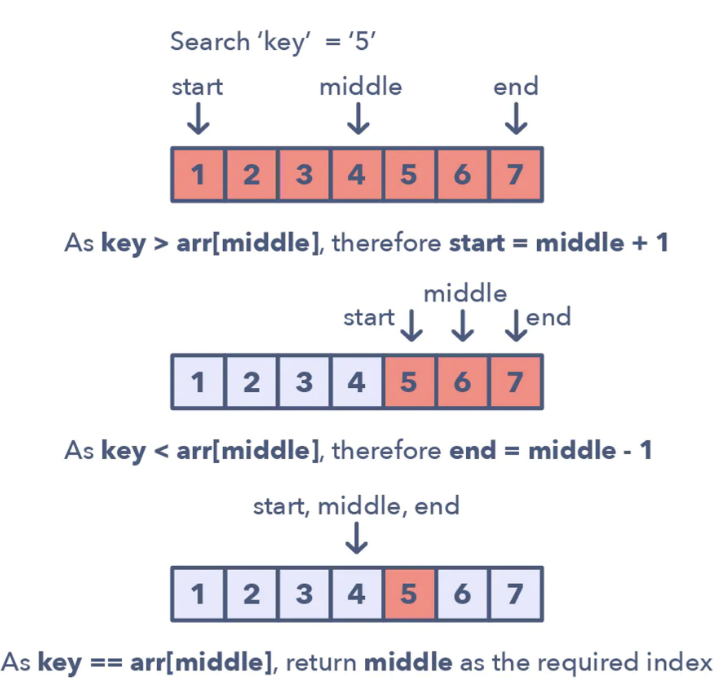
The basic idea of binary search is simple, we perform a search between the start and end pointer.

The steps for searching:

1. We pick a middle
2. We compare this middle number with our target:
   • if middleNumber == target: we found a solution
   • if middleNumber < target: which means we have to search on the right space
     • start = middle + 1
   • if middleNumber > target: which means we have to search on the left space
     • end = middle - 1

Condition:

• For binary search to work, the array has to be sorted* (this is not always true, see index and range below)

Ways to identify

• When there is a search space. Note that a search space could be index or range
  • index: index is quite obvious, when the array is sorted in 1 direction, we can use the index as the search space
  • range: range is the range from the smallest and the largest. This can work when the array is unsorted. For example, given a range of day, a smallest and largest number.
    • See: https://leetcode.com/problems/find-the-duplicate-number/
• If you notice that if condition(x) is True, then condition(x+1) is also True

Time complexity

• $O(logn)$ since we go half half every single time

Space complexity

• $O(1)$

Picking a middle

For Python it's easy, we can just do

mid = (start + end) // 2

For Java and C++, if start and end is too large, it might trigger Integer overflow. Therefore we are doing this

mid = start + (end - start) // 2

or if you want a fancy bitwise

mid = start + ((end - start) >> 1)

public static int binarySearch(List<Integer> array, Integer target) {
  int startIndex = 0;
  int endIndex = array.size() - 1;

  while (startIndex < endIndex) {
    int middleIndex = startIndex + (endIndex - startIndex) / 2;

    if (array.get(middleIndex) >= target) {
      endIndex = middleIndex;
    } else {
      startIndex = middleIndex + 1;
    }
  }

  return startIndex;
}

Advance binary search

Considering this template

def binary_search(array) -> int:
    def condition(value) -> bool:
        pass

    left, right = min(search_space), max(search_space) # could be [0, n], [1, n] etc. Depends on problem
    while left < right:
        mid = left + (right - left) // 2
        if condition(mid):
            right = mid
        else:
            left = mid + 1
    return left

For this binary search to work, you need to define the search space as following

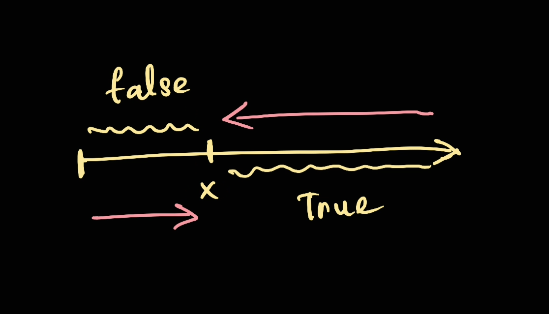
On the search space, there is a point x such that:

• Everything on the left handside of x will be False
  • Therefore, it needs to converge to x which means to go to the right
  • Because of that we have left = mid + 1 in else
• Everything on the right handside of x will be True
  • Therefore, it needs to converge to x which means to go to the left
  • Because of that, right = mid if the condition is True

In the end, left will be the cut point (x) which is the minimum point on the search space that satisfies condition(x)

How to find the search space

The search space normally is what you're looking for. Note: the search space needs to contains all the possible solutions

How to write the condition function

The condition function needs to satisfy the condition of the question.
Note that the question will have 2 different condition:

1. One condition for the search space (normally find a minimum x such that ...)
2. Another condition is for the condition function this is normally within k number of days, forming k groups
   • Sometimes the condition is hidden and we have to think of the condition itself. Following this template, this is the only thing we have to do

Example

Let's analyse someof the example

278. First Bad Version [Easy]

You are a product manager and currently leading a team to develop a new product. Since each version is developed based on the previous version, all the versions after a bad version are also bad. Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad. You are given an API bool isBadVersion(version) which will return whether version is bad

Example

Given n = 5, and version = 4 is the first bad version.

call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true

Then 4 is the first bad version. 

Search Space
The bold in here is what we want to look for, "first bad version". So the version will be the search space.

Note that in here we're returning the version as well.

Condition
This one is easy, they already provided a condition function which is isBadVersion. Let's visualise it like this:

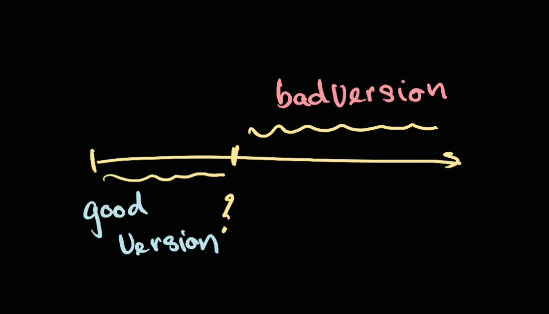
Therefore it's just

class Solution:
    def firstBadVersion(self, n) -> int:
        left, right = 1, n
        while left < right:
            mid = left + (right - left) // 2
            if isBadVersion(mid):
                right = mid
            else:
                left = mid + 1
        return left

69. Sqrt(x) [Easy]

Implement int sqrt(int x). Compute and return the square root of x, where x is guaranteed to be a non-negative integer. Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.

Example

Input: 4
Output: 2

Search space
In here we want to search for a number such that it's a square root of x. Therefore the search space is from $1 \rightarrow x$

Condition
Let call this number we're looking for is k, then the condition will be k * k >= x

def mySqrt(x: int) -> int:
    left, right = 0, x
    while left < right:
        mid = left + (right - left) // 2
        if mid * mid > x:
            right = mid
        else:
            left = mid + 1
    return left - 1 

Note: this question we use mid * mid > x just to satisfy the condition of the question, so basically the question is asking you to round down. So for example $2.828...^2 = 8$ but it takes 2 as the answer. But $2^2 = 4$ right?

It's just the question asking like that, so basically we need to adjust our search space in the way that everything on the right is strictly > $x$

So the one on the left is either

• What we're looking for exact answer when mid * mid == x
• Or the round down of $2.828...^2 = 2$

35. Search Insert Position [Easy]

Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order. You may assume no duplicates in the array.

Example

Input: [1,3,5,6], 5
Output: 2

Search space
We want to return the index. Therefore the search space is the indices in this array, from $0 \rightarrow len(arr)$

Condition
Condition is simple, if we want to find the index for a target, everything on the right handside has to be >= than the target. If doing so the target will be placed in a correct position of a sorted array

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] >= target:
                right = mid
            else:
                left = mid + 1
        return left

1011. Capacity To Ship Packages Within D Days [Medium]

A conveyor belt has packages that must be shipped from one port to another within D days. The i-th package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.

Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within D days.

Example

Input: weights = [1,2,3,4,5,6,7,8,9,10], D = 5
Output: 15
Explanation: 
A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10

Search space
The question asking for the weight capacity, so the search space will be weight capacity from $max(weights) \rightarrow sum(weights)$

Condition
Note how it says "within D days". So the condition needs to be smaller or equals (<=) than D days

def shipWithinDays(weights: List[int], D: int) -> int:
    def feasible(capacity) -> bool:
        days = 1
        total = 0
        for weight in weights:
            total += weight
            if total > capacity:  # too heavy, wait for the next day
                total = weight
                days += 1
                if days > D:  # cannot ship within D days
                    return False
        return True

    left, right = max(weights), sum(weights)
    while left < right:
        mid = left + (right - left) // 2
        if feasible(mid):
            right = mid
        else:
            left = mid + 1
    return left

The condition function is a bit hard to write but that's the only place you have to think. Plus you've already know what it should return as True and False

875. Koko Eating Bananas [Medium]

Koko loves to eat bananas. There are N piles of bananas, the i-th pile has piles[i] bananas. The guards have gone and will come back in H hours. Koko can decide her bananas-per-hour eating speed of K. Each hour, she chooses some pile of bananas, and eats K bananas from that pile. If the pile has less than K bananas, she eats all of them instead, and won't eat any more bananas during this hour.

Koko likes to eat slowly, but still wants to finish eating all the bananas before the guards come back. Return the minimum integer K such that she can eat all the bananas within H hours.

Example

Input: piles = [3,6,7,11], H = 8
Output: 4

Search Space
What are we looking for? We're looking for k banana/hour. So the search space should be banana/hour from $1 \rightarrow \max(piles)$

Why from $1$ why not $\min(piles)$. Well $\min(piles)$ could possibly work as well but remember we want the search space to contain all possible solution

Condition
We have two condition here, we only focus on the within H hours as that's the condition we're looking for our condition() function. Looking for a minimum integer K but is the search space condition.

So condition is within H. So we just need to make sure hours <= H

So the condition is something like follows:

def condition(self, speed: int, piles: List[int], h: int) -> bool:
	hours = 0

	for banana in piles:
			timeTaken = ceil(banana/speed)
			hours += timeTaken
			if hours > h: return False

	return hours <= h

def minEatingSpeed(piles: List[int], H: int) -> int:
    def feasible(speed) -> bool:
        # return sum(math.ceil(pile / speed) for pile in piles) <= H  # slower        
        return sum((pile - 1) // speed + 1 for pile in piles) <= H  # faster

    left, right = 1, max(piles)
    while left < right:
        mid = left  + (right - left) // 2
        if feasible(mid):
            right = mid
        else:
            left = mid + 1
    return left

1482. Minimum Number of Days to Make m Bouquets [Medium]

Given an integer array bloomDay, an integer m and an integer k. We need to make m bouquets. To make a bouquet, you need to use k adjacent flowers from the garden. The garden consists of n flowers, the ith flower will bloom in the bloomDay[i] and then can be used in exactly one bouquet. Return the minimum number of days you need to wait to be able to make m bouquets from the garden. If it is impossible to make m bouquets return -1.

Example

Input: bloomDay = [1,10,3,10,2], m = 3, k = 1
Output: 3
Explanation: Let's see what happened in the first three days. x means flower bloomed and _ means flower didn't bloom in the garden.
We need 3 bouquets each should contain 1 flower.
After day 1: [x, _, _, _, _]   // we can only make one bouquet.
After day 2: [x, _, _, _, x]   // we can only make two bouquets.
After day 3: [x, _, x, _, x]   // we can make 3 bouquets. The answer is 3.

Search space
Search space asking for minimum number of days, so it's obviously days. Therefore we need $\min(bloomDay) \rightarrow \max(bloomDay)$

Condition
To make m bouquets, so our condition needs to be making at least m bouquets (making more is fine right?) so bouquets >= m. To guarantee that on the right handside of search space we always have true

def minDays(bloomDay: List[int], m: int, k: int) -> int:
    def feasible(days) -> bool:
        bonquets, flowers = 0, 0
        for bloom in bloomDay:
            if bloom > days:
                flowers = 0
            else:
                bonquets += (flowers + 1) // k
                flowers = (flowers + 1) % k
                # or if the Math is too hard:
                # flowers += 1
                # if bonquets == k:
				#    flowers = 0
				#    bonquets += 1
        return bonquets >= m

    if len(bloomDay) < m * k:
        return -1
    left, right = 1, max(bloomDay)
    while left < right:
        mid = left + (right - left) // 2
        if feasible(mid):
            right = mid
        else:
            left = mid + 1
    return left