Binary Search In Rotated Sorted Array

Question

There is an integer array nums sorted in ascending order (with distinct values).

Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].

Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.

You must write an algorithm with O(log n) runtime complexity.

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Input: nums = [1], target = 0
Output: -1

Constraints:

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• All values of nums are unique.
• nums is an ascending array that is possibly rotated.
• -104 <= target <= 104

Solution

For this question there are 3 possible scenarios:

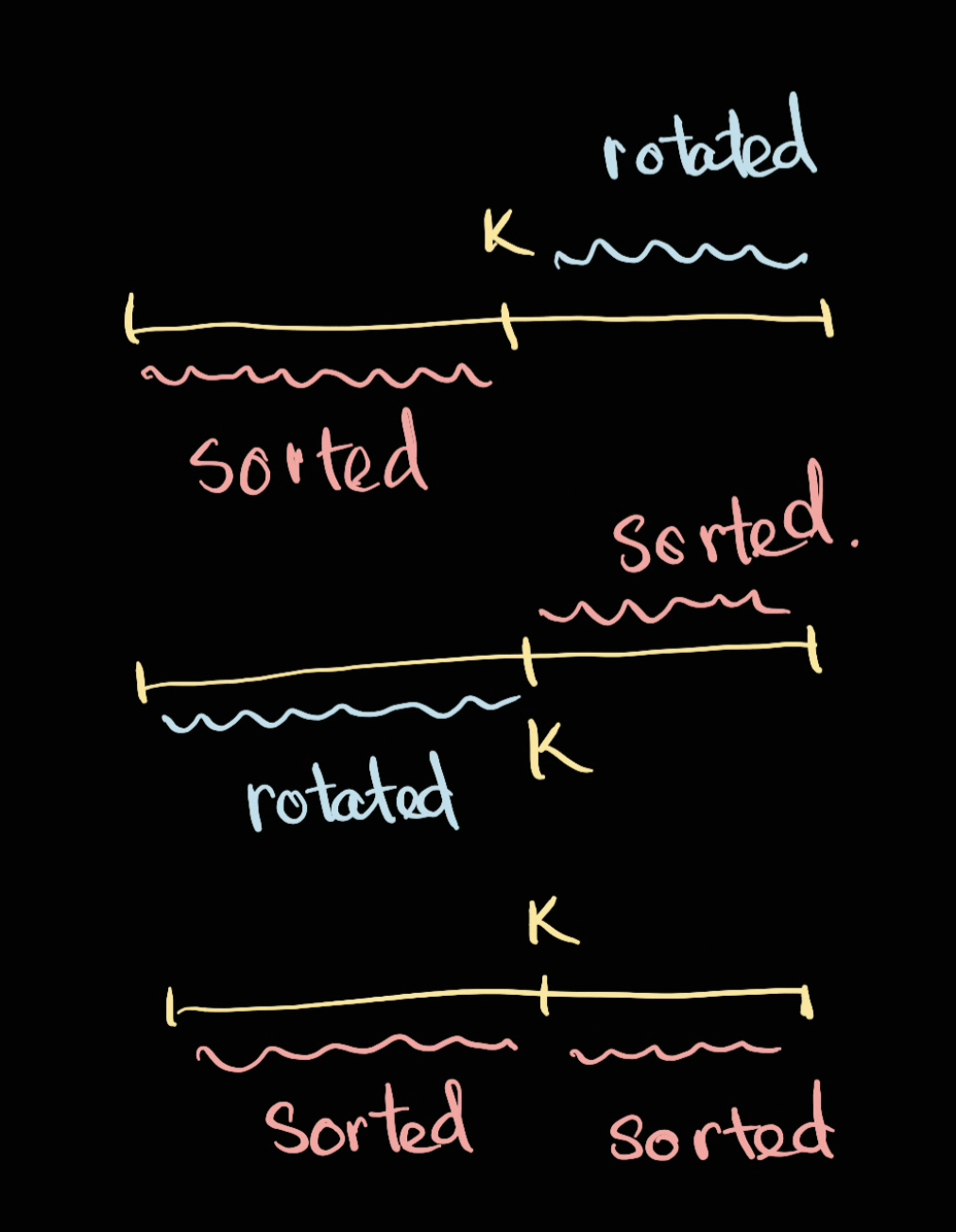
Given a pivot point $K$, the scenarios are:

1. The left handside is sorted and right hand side is rotated. For example [7,8,9,|1|,2,3,4] is a rotated on the right hand side
2. The left handside is rotated, the right hand side is sorted. For example [7,8,9,0,1,|2|,3,4,5,6]
3. There is no rotation: left handside is sorted and right handside is sorted as well. For example [1,2,3,|4|,5,6,7,8]

Note:

• The |x| denotes the middle point.
• There is no condition the whole array is rotated due to the requirements of the question.

Implementation

When looking for element x, we want to determine if x is in the sorted array. We can determine this since the array is sorted. Else we will just search in the rotated space.

class App:
    def search(self, nums: List[int], target: int) -> int:
        if len(nums) == 0: return -1
        
        left, right = 0, len(nums) - 1
        while left <= right: 
            mid = (left + right) // 2
            
            if nums[mid] == target: 
                return mid
            
            rightSorted = nums[mid] < nums[left] # Mid is supposed to be > left normally, so left rotated
            leftSorted = nums[mid] > nums[right] # Mid is supposed to be < right normally, so right rotated
            
            if rightSorted:
                # We can determine if element is on the right
                if target > nums[mid] and target <= nums[right]:
                    # Search on the right
                    left = mid + 1
                else:
                    # if not on the right then on the rotated path
                    right = mid - 1
            elif leftSorted:
                # We can determine if element is on the left
                if target >= nums[left] and target < nums[mid]:
                    # Search on the left
                    right = mid - 1
                else:
                    # if not on the left then on the rotated path
                    left = mid + 1
            else:
                # Normal, no rotation
                if target < nums[mid]:
                    right = mid - 1
                else:   
                    left = mid + 1
        return -1

If the array is normal, the following condition has to hold true:

nums[left] < nums[mid] < nums[right]

If nums[mid] < nums[left]: which means left is rotated
If nums[mid] > nums[right]: which means right is rotated

Note: in here we're not counting mid is part of the left group or the right group. However we'll discuss this in optimisation

Time Complexity: $O(logn)$
Space Complexity: $O(1)$

Optimisation

There is not much to optimise here except for code style.

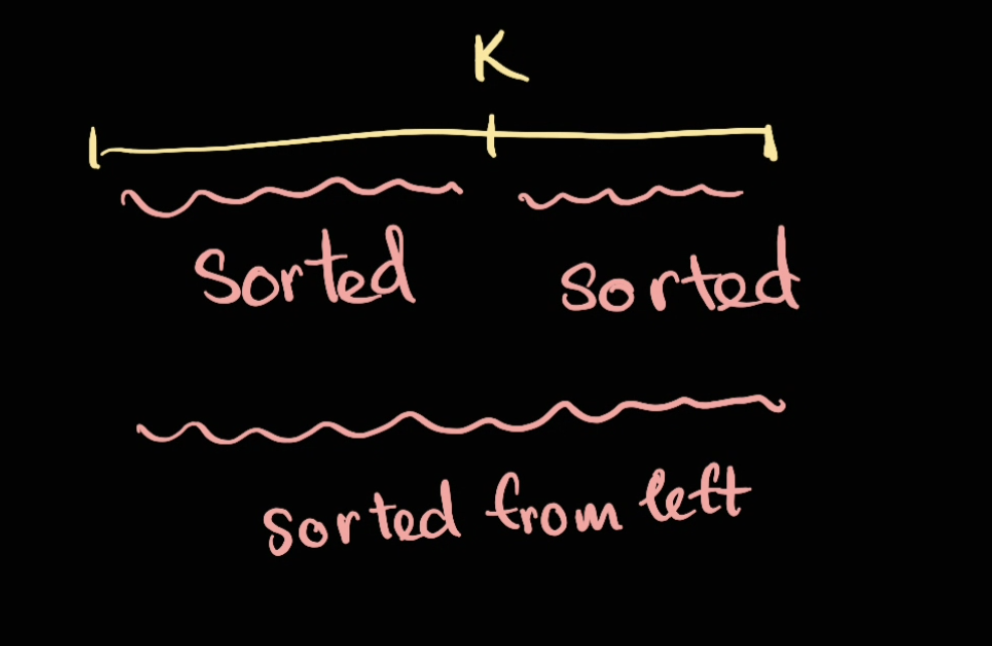
If you really think about it, there is actually only 2 scenarios:

• leftSorted
• rightSorted

We can just simply combine the no rotation as leftSorted. Why? The condition of them is the same:

For no rotation, we do a normal binary search:

if target < num_at_mid:
	search_left
else:
	search_right

This logic is also applicable for leftSorted as well:

if target > nums_left and target < num_at_mid:
	search_left
else:
	search_right

Well if you think about it, if there is no rotation, of course target > nums_left.

So we have the final shortened code:

class App:
    def search(self, nums: List[int], target: int) -> int:
        if len(nums) == 0: return -1
        
        left, right = 0, len(nums) - 1
        while left <= right: 
            mid = (left + right) // 2
            
            if nums[mid] == target: 
                return mid
            
            rightSorted = nums[mid] < nums[left]
            
            if rightSorted:
                # We can determine if element is on the right
                if target > nums[mid] and target <= nums[right]:
                    # Search on the right
                    left = mid + 1
                else:
                    # if not on the right then on the rotated path
                    right = mid - 1
            else:
                # We can determine if the element is on the left
                if target >= nums[left] and target < nums[mid]:
                    # Search on the left
                    right = mid - 1
                else:
                    # if not on the left then on the rotated path
                    left = mid + 1
        return -1