Spiral Traversal

Sometimes we want to traverse in spiral, for example

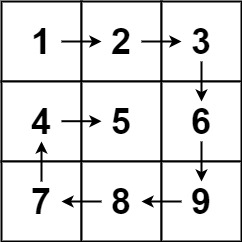
Or

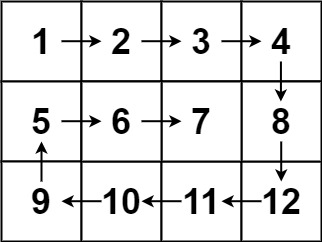
For example: 54. Spiral Matrix

DFS based traversal

The idea is like going through a DFS in a map. For this we will have to mark each cell as we go.

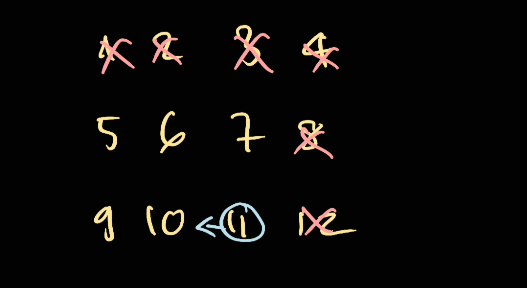
For example:

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        VISITED = "X"
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        currentDirection = 0

        m, n = len(matrix), len(matrix[0])
        ans = []

        if (m == 0 and n == 0): return ans

        x,y = 0, 0

        while (True):
            ans.append(matrix[x][y])
            matrix[x][y] = VISITED  

            dx, dy = directions[currentDirection % len(directions)]
            
            if ((x + dx >= m or y + dy >= n) or matrix[x + dx][y + dy] == VISITED):
	            # Change the direction
                currentDirection = (currentDirection + 1) % len(directions)

                dx, dy = directions[currentDirection]
                if ((x + dx >= m or y + dy >= n) or matrix[x + dx][y + dy] == VISITED): 
					# If after changing direction already and we still cannot go, we have finished the traversal
	                break

            x += dx
            y += dy

        return ans

Time Complexity: $O(n \times m)$
Space Complexity: $O(1)$

However we need to modify the current array

4 pointers based algorithm

This is the same thing as Array rotation > Approach 2: Loop using 4 pointers.

Now there are 2 ways of doing it.

Pattern 1: Traverse only up to last element (not the whole line)

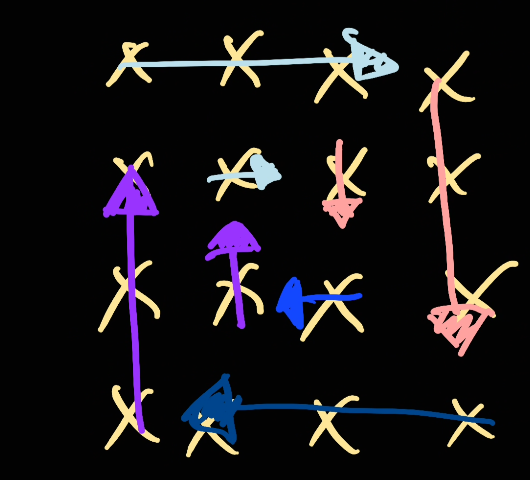
As we can see we only traverse up to the last element (we don't cross out the whole role). Doing this will look intuiative. After the whole traversal, we shift the boundary inside.

So the first iteration will look like this:

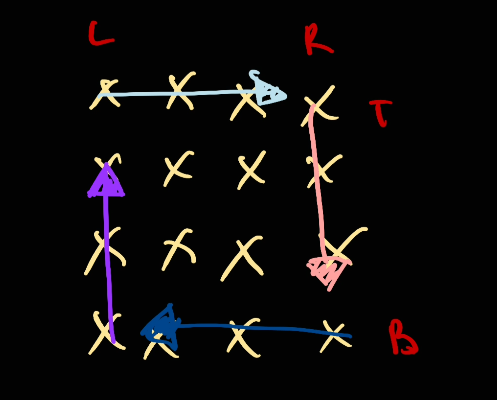
After finishing this loop, we shift everything in side, so the boundary will look like as following:

And we complete the inner cycle loop:

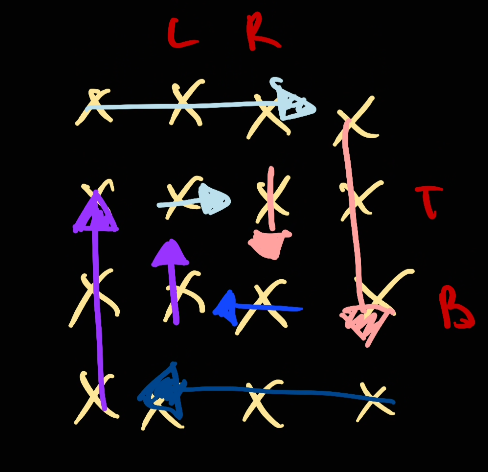
Problem:

However, doing this will create some edge cases:

Problem 1: Miss out the center element
Since we are only traversing from [left, right) (not including right), the first edge cases we have is we will leave out the center element. For example: ^b9ca21

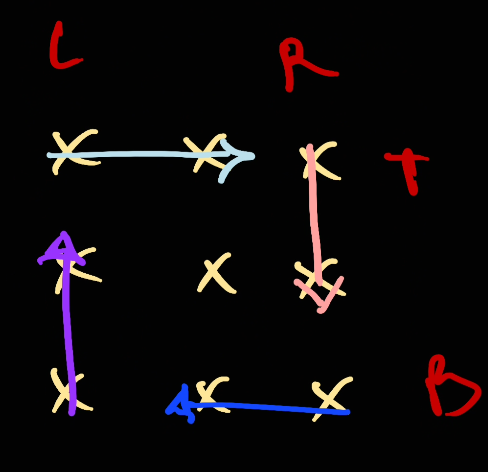
Now after this, 4 pointers will go down to close the boundary:

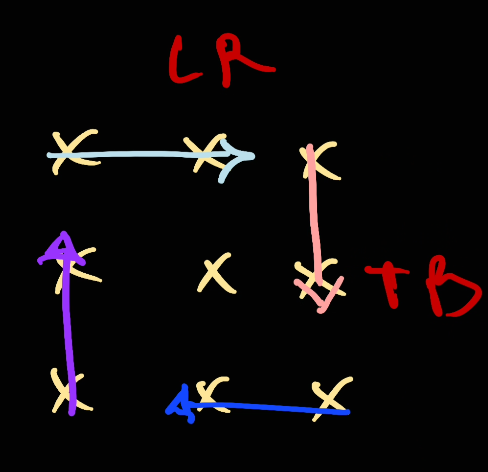
However, since we're only looping from [left, right). We will not take this element.

Problem 2: Middle line edge case
For example if we have a middle line:

Next we will close in the boundaries

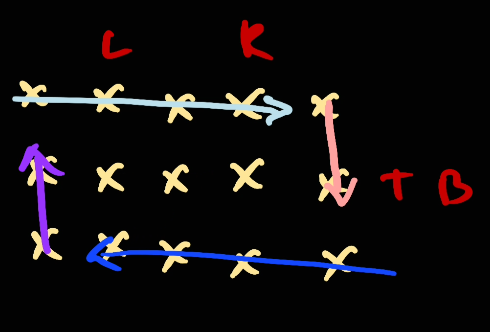
Since we only loop from [left, right). We will go as following:

• 1. [left, right)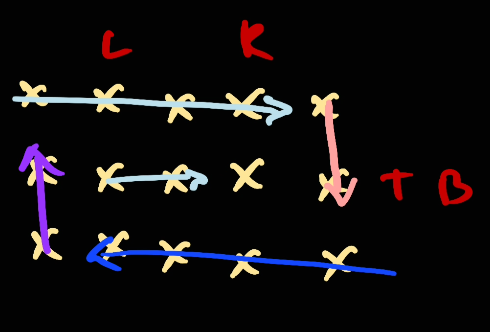
• 2. Skip top to bottom because [top, bottom) results in no move
• 3. Go [right, left)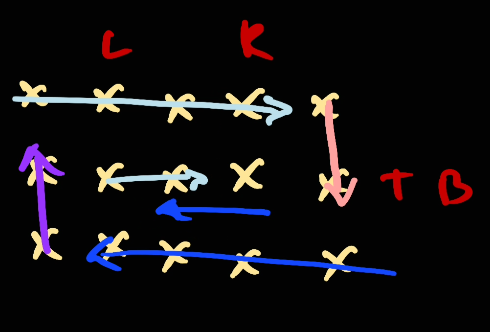
     As the result, it makes our middle element duplicate. Therefore, we need to check if we don't have [top, bottom), we would move right only once to cover the last element.

The same thing would happen for left and right vertically

The code

class App:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if len(matrix) == 0: return []
        if len(matrix) == 1: return matrix[0]

        result = []

        left, right = 0, len(matrix[0]) - 1
        top, bottom = 0, len(matrix) - 1
        while left <= right and top <= bottom:
            
            for i in range(right - left):
                result.append(matrix[top][left + i])
            
            for i in range(bottom - top):
                result.append(matrix[top + i][right])
                
            for i in range(right - left):
                result.append(matrix[bottom][right - i])
				# edge case middle line horizontal
                if (bottom == top):
                    break

            for i in range(bottom - top):
                result.append(matrix[bottom - i][left])
				# edge case middle line vertical
                if (left == right):
                    break
            
            left += 1
            top += 1
            bottom -= 1
            right -= 1

		# Handle the center edge case
        if len(matrix) == len(matrix[0]) and len(matrix) % 2 != 0:
            mid = len(matrix) // 2
            result.append(matrix[mid][mid])
        
        return result

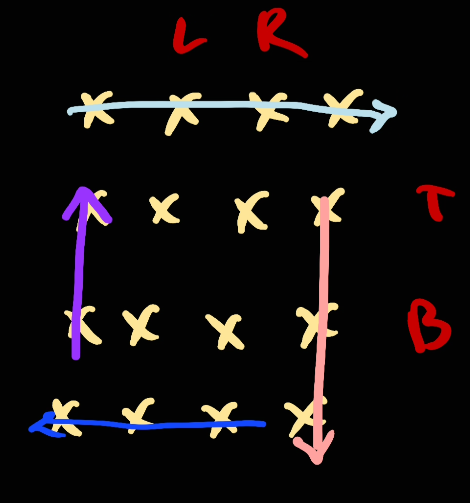
Pattern 2 (Recommend): Traverse the whole role and move boundary in order

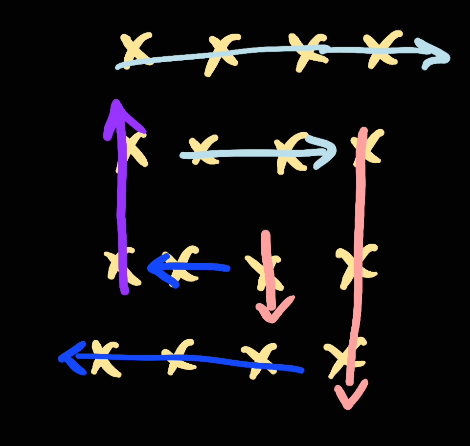
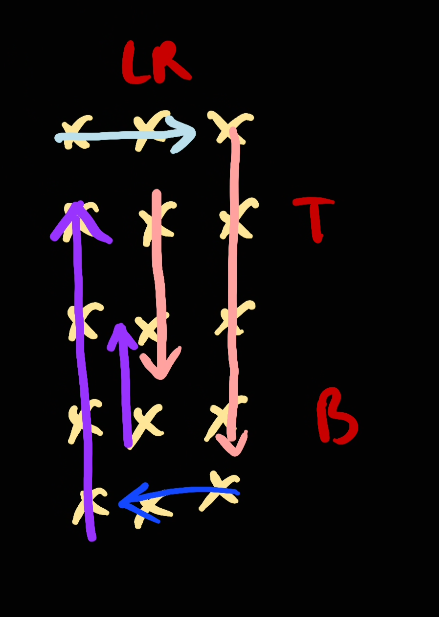
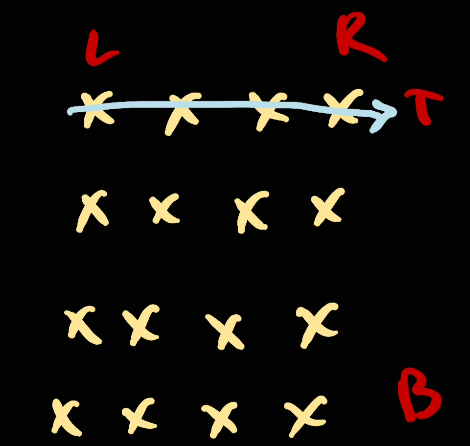
So everytime we go, we go up to the last element as possible before changing the direction. So given the boundary like this:

Now we're going to move [left, right] (right inclusive).

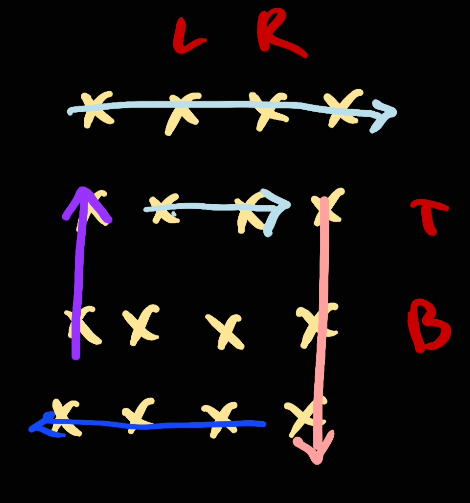
Now since we've already crossed the corner element of [right, top], we will need to move top down and go from top to bottom:

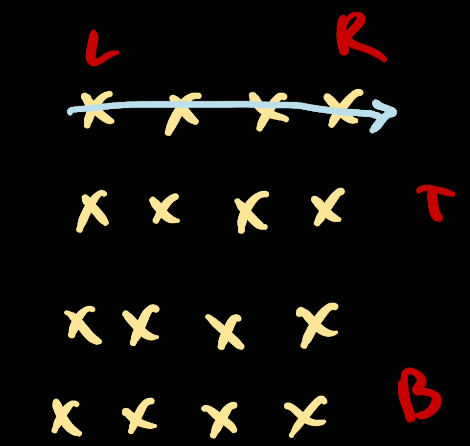
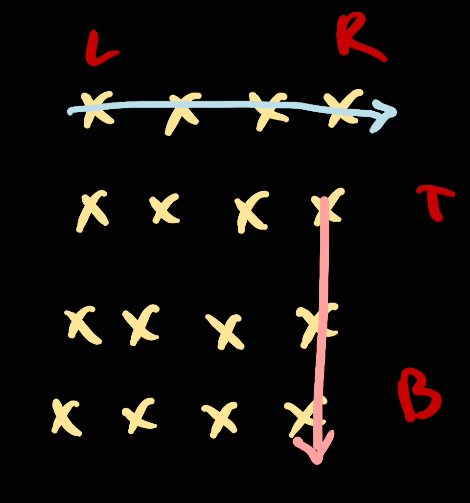
Next, we move right to left

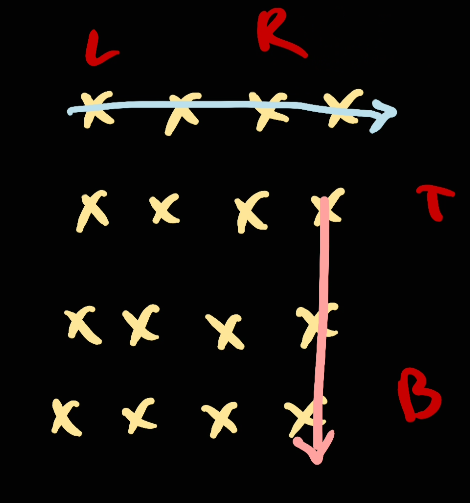
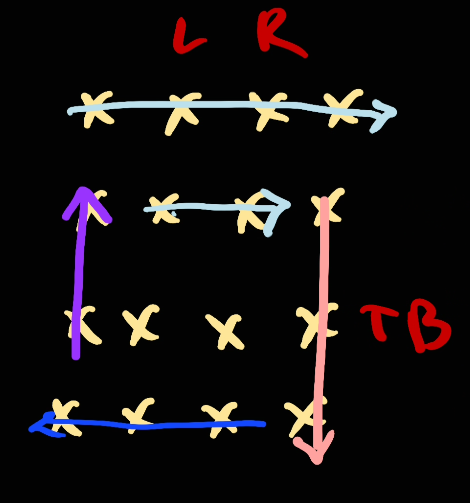
And we go [right, left]

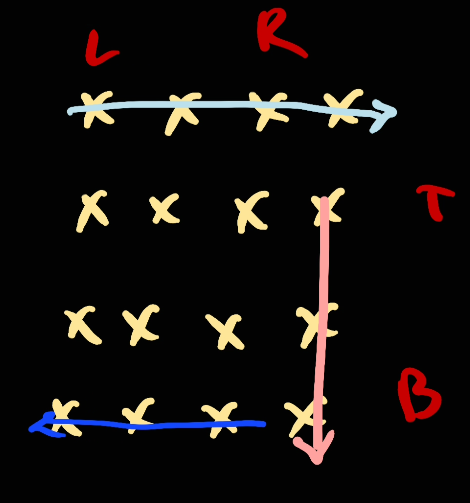
Next, move bottom up

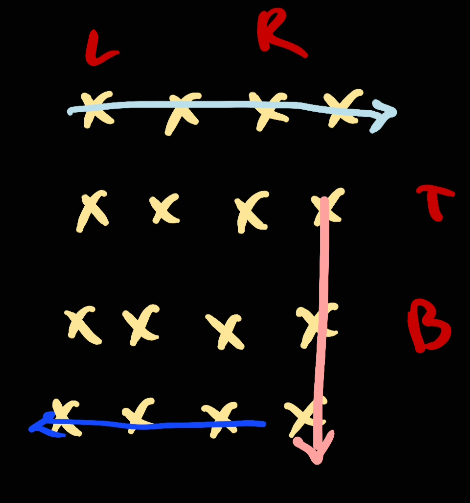
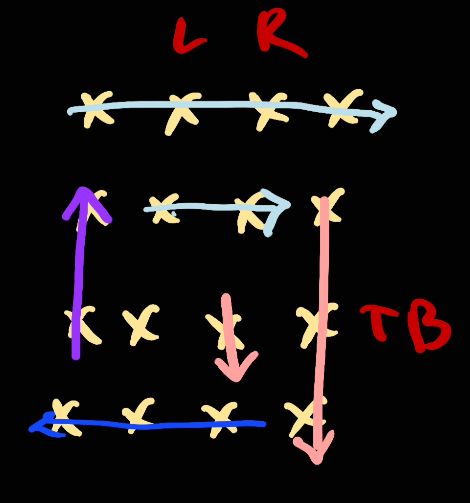
Then we go [bottom, top]

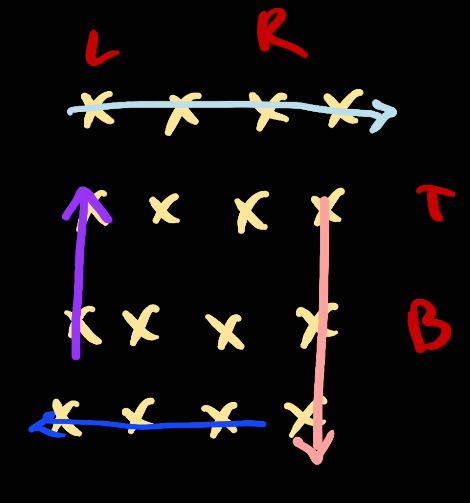
Next we move left to to right and repeat from the start:

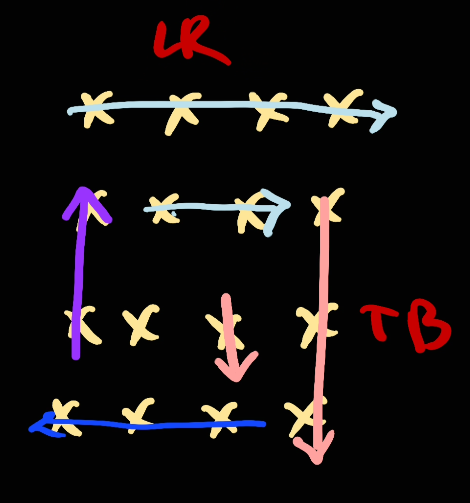
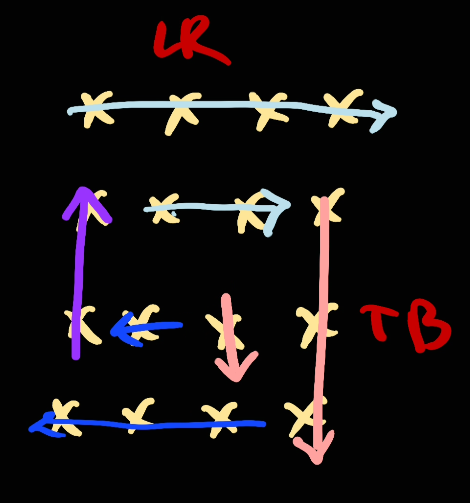
Edge cases

For problem 1, this wont happen as the algorithm itself will take [left, right] or `[top, bottom]:

So just before we finish getting all the around, this is what we have

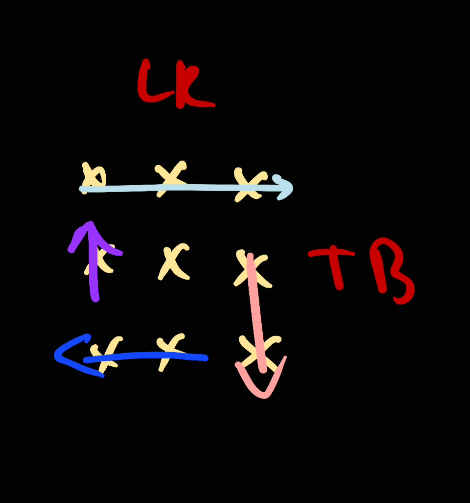
For this center element, the algorithm will still take it as we take [left, right]:

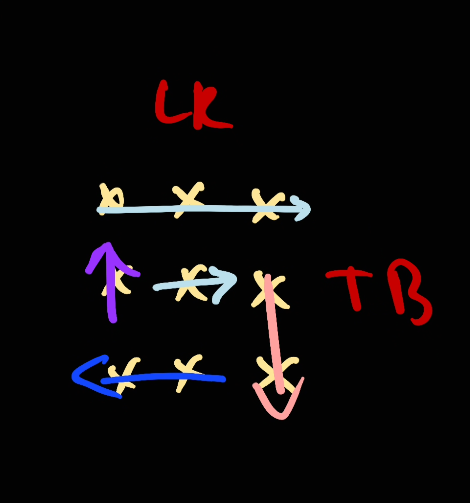
After doing that, top will go down as of the algorithm

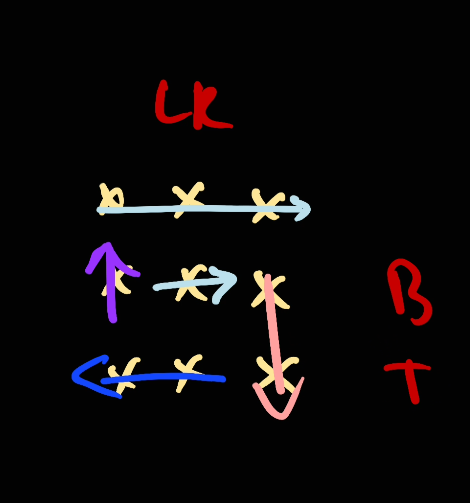
Since the range [top, bottom] is not valid anymore, we move right to the left as part of the algorithm

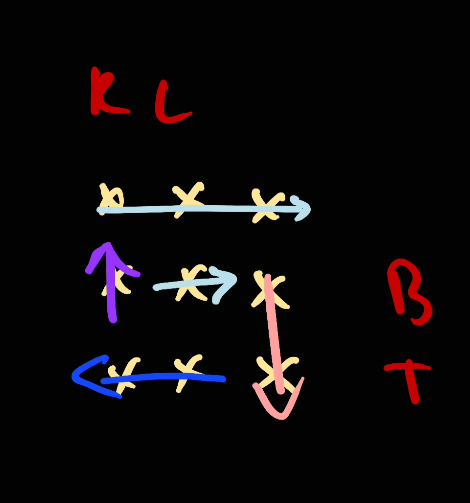
As [right, left] is not a valid range anymore, we will not take any element here.

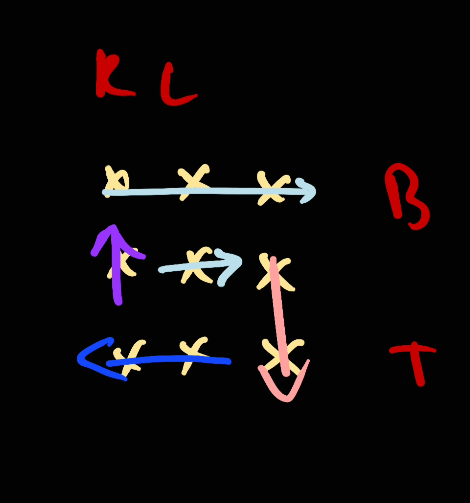
Bottom will go up as part of the algorithm, however the range [bottom, top] is not valid anymore so we're not taking anything here.

Similarly for left

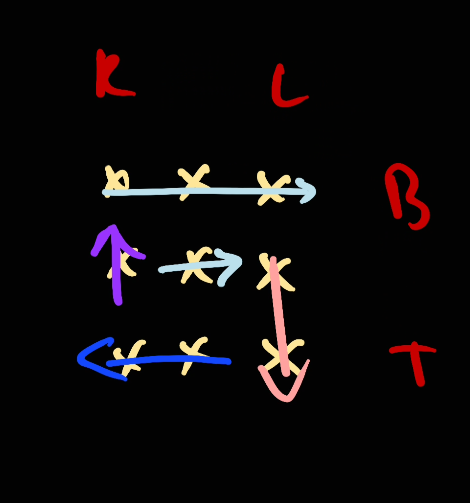
For problem 2, we will have to do edge case handling

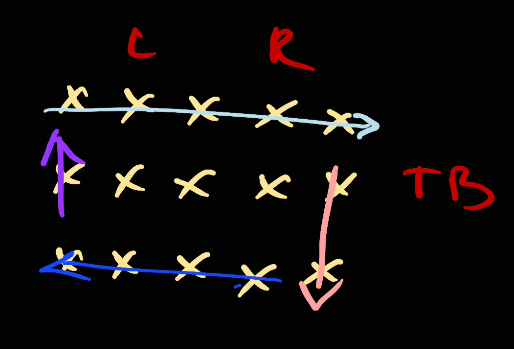
Now, since we take [left, right] we will take the whole line.

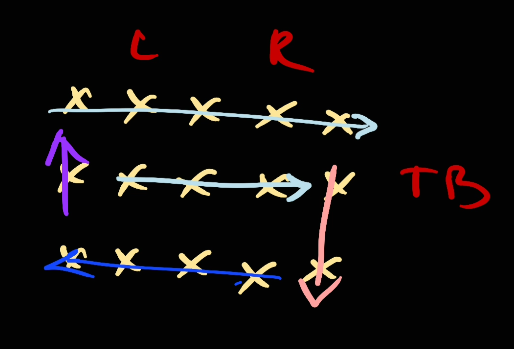
Next, top will go down as of the algorithm

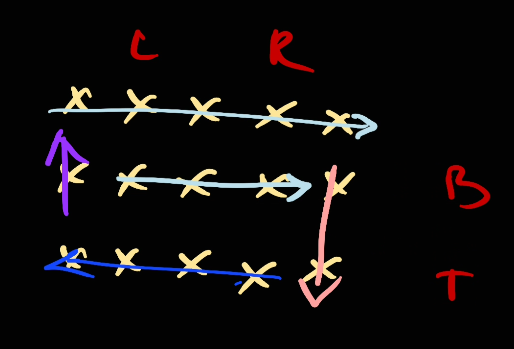
the range [top, bottom] is negative so we're not adding anything here. Next we move right to the left as part of the algorithm

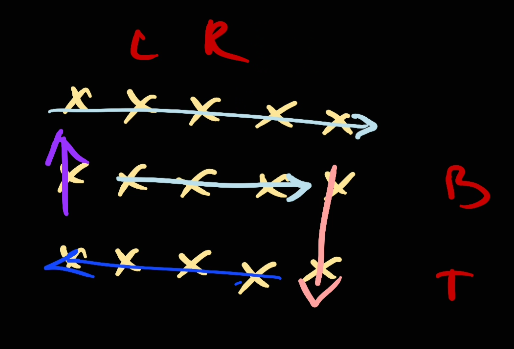
Now, we will take [right, left].

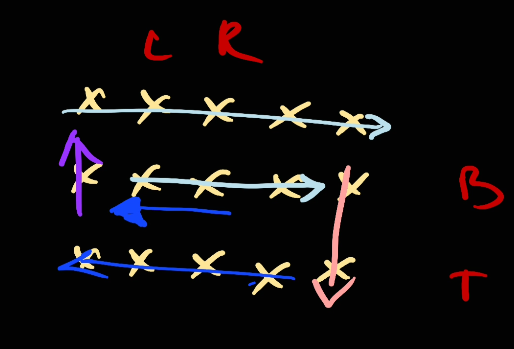
However as you see, there will be a problem here. This happen when top > bottom, as a result we only have 1 line and the previous loop from [left, right] should went through this already.

Similar problem in vertical case. Therefore it's important to terminate the algorithm when there is 1 line left in the second half when going from right to left or bottom to top

The code

class App:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if len(matrix) == 0: return []
        if len(matrix) == 1: return matrix[0]

        result = []

        left, right = 0, len(matrix[0]) - 1
        top, bottom = 0, len(matrix) - 1
        while left <= right and top <= bottom:
            
            for i in range(right - left + 1):
                result.append(matrix[top][left + i])
            top += 1
            
            for i in range(bottom - top + 1):
                result.append(matrix[top + i][right])
            right -= 1
                
            if left > right or top > bottom:
	            # edge case middle line
                break
            
            for i in range(right - left + 1):
                result.append(matrix[bottom][right - i])
            bottom -= 1

            for i in range(bottom - top + 1):
                result.append(matrix[bottom - i][left])
            left += 1
        
        
        return result