Array Rotation

Question statement

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise) in-place

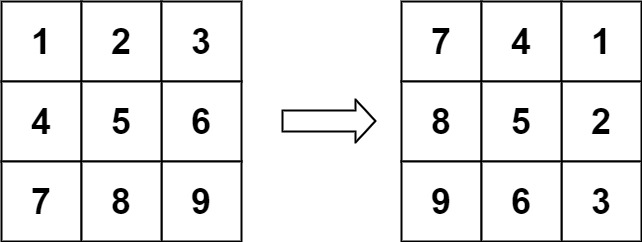
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

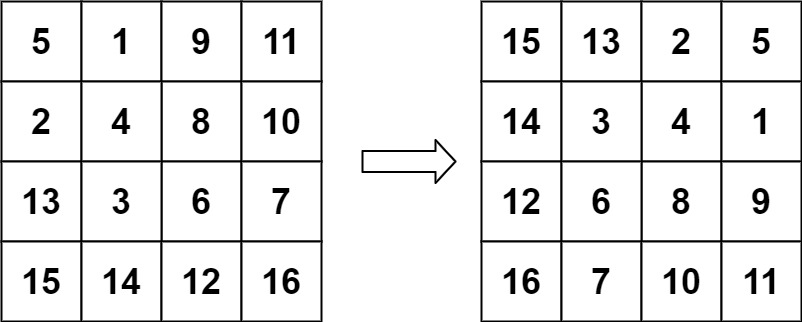
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Example: https://leetcode.com/problems/rotate-image/

Approach 1: Loop using 2 pointers

Time complexity: $O(n)$:

• Looping from the outer ring to the inner ring. Each cell is written once
  Space complexity: $O(1)$:
• In-place modification

The idea is we have j to loop for each element. Whereas i to go level-by-level.

Therefore, the start elements will be from i to n-i with n is the last element. This will be the boundary of our loop: [i, n-i].

class App:
    def rotate(self, matrix: List[List[int]]) -> None:
        if len(matrix) == 0: return []
        if len(matrix) != len(matrix[0]):
            raise RuntimeError("Invalid dimension")
        
        n = len(matrix) - 1
        for i in range(len(matrix)): # Loop through level from outside to inside
            for j in range(i, len(matrix) - i - 1): # each element inside the ring
                top = matrix[i][j]
                right = matrix[j][n - i]
                bottom = matrix[n - i][n - j]
                left = matrix[n - j][i]
                
                matrix[j][n - i] = top
                matrix[n - i][n - j] = right
                matrix[n - j][i] = bottom
                matrix[i][j] = left

        return matrix

Approach 2: Loop using 4 pointers

The idea is we have 4 pointers:

• top, bottom, left, right

l     r
* * * * t
* * * *
* * * *
* * * * b

we can then keep moving these 4 pointers to swap to each other

Time complexity: $O(n)$

• Loop using 4 pointers in 4 corners, each cell is written once
  Space complexity: O(1)
• In place modification

 def rotate(self, matrix: List[List[int]]) -> None:
        if len(matrix) == 0: return []
        if len(matrix) != len(matrix[0]):
            raise RuntimeError("Invalid dimension")
        
        top, bottom = 0, len(matrix) - 1
        left, right = 0, len(matrix) - 1
        
        while (left < right):
            for i in range(right - left): 
                topElement = matrix[top][left + i] # row is fixed to top, column moves
                rightElement = matrix[top + i][right] # column is fixed to right, row moves
                bottomElement = matrix[bottom][right - i] # row is fixed to bottom, column moves
                leftElement = matrix[bottom - i][left] # column is fixed to left, row moves
                
                matrix[top + i][right] = topElement
                matrix[bottom][right - i] = rightElement
                matrix[bottom - i][left] = bottomElement
                matrix[top][left + i] = leftElement
                
                
            top += 1
            left += 1
            right -= 1
            bottom -= 1
        
        return matrix