Merge K Sorted Lists

Question

You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.

Merge all the linked-lists into one sorted linked-list and return it.

Example

Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
  1->4->5,
  1->3->4,
  2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6

Input: lists = []
Output: []

Input: lists = [[]]
Output: []

Solution

General idea

The idea in here is quite obvious, we can start with a dummy linkedlist and then keep adding the minimum of the three linkedlist.
Everytime we add, we will shift the pointer of that list.

For example:

1. We start with a dummy head with our linked list. We then consider which element is the smallest. So in here we have either of these 1 is the smallest: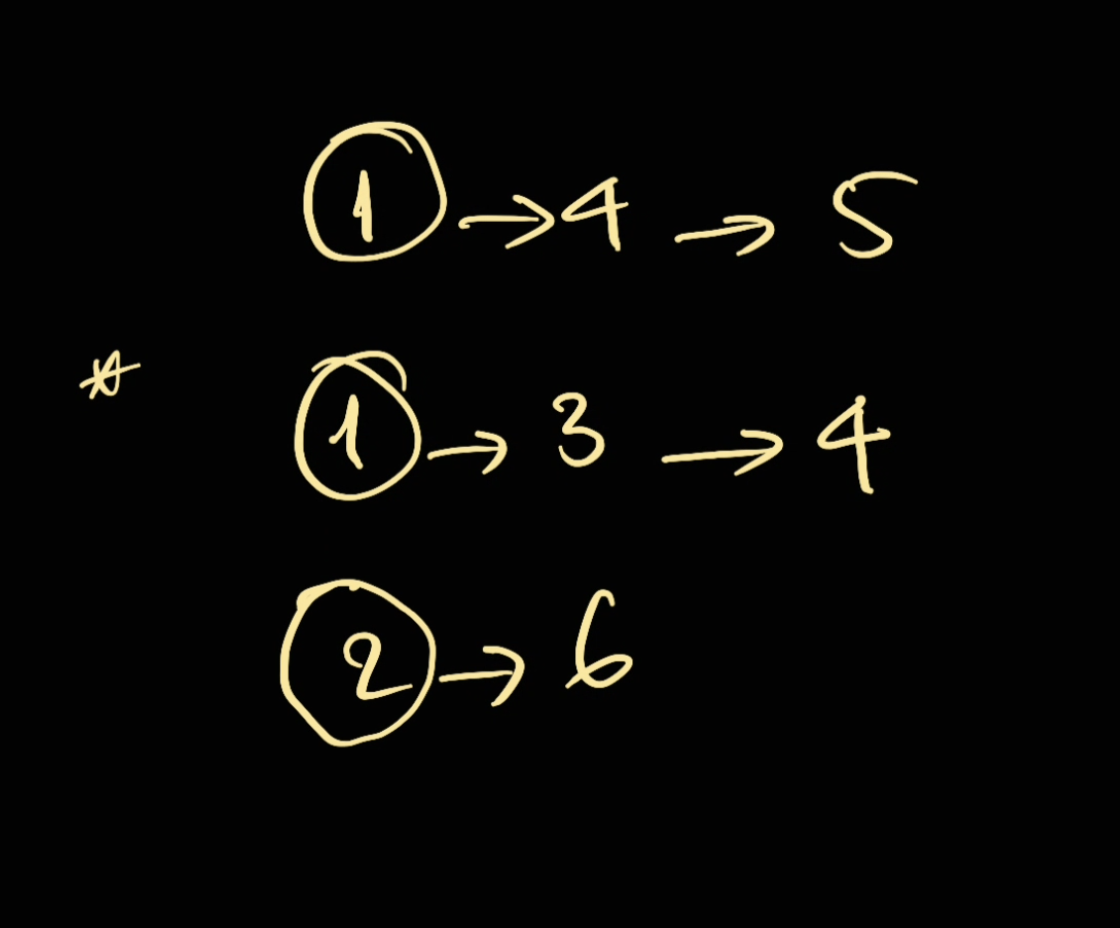
2. We can pick either of them is fine, and then we will connect our dummy * to that list and then look for the next smallest: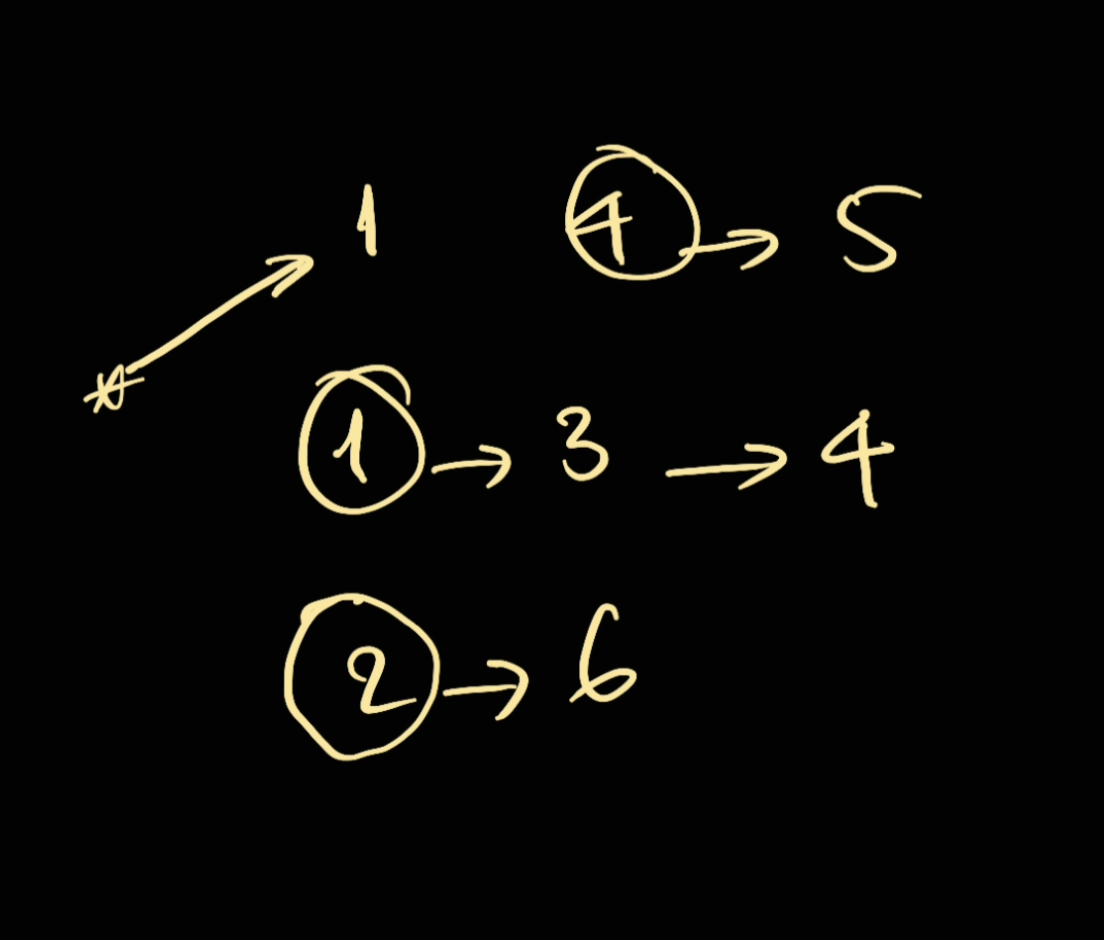
3. In here we will choose the other 1. When choosing the other 1, we also increase the pointer of that node: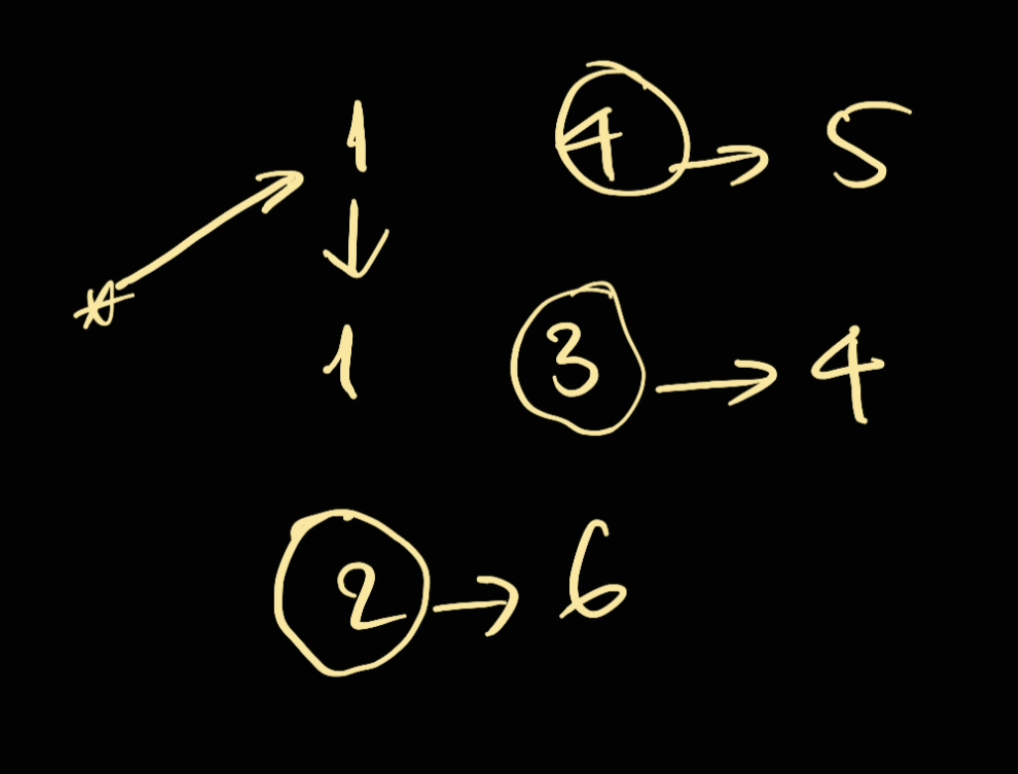
4. Now we will choose 2 as our next node, the algorithm keeps going until it cannot

How to find which list has the smallest node

Another question we need to ask is to find the smallest node in the list. In our case, we have k list. We cannot loop through these k elements every single time.

A good way to deal with this situation is to use a Min heap to keep track of the smallest element. And then we keep adding new element to the heap whenever there is one

Implementation

class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        minHeap = []
        mergedHead = ListNode()

        for head in lists:
            if not head: continue
            heapq.heappush(minHeap, (head.val, id(head), head))
        
        currHead = mergedHead

        while minHeap:
            minValue, _, minNode = heapq.heappop(minHeap)

            currHead.next = minNode
            currHead = currHead.next

            nextNode = minNode.next
            if nextNode:
                heapq.heappush(minHeap, (nextNode.val, id(nextNode), nextNode))
        
        return mergedHead.next

Time complexity: $O(nlogk)$

• With $n$ is the total number of items in the list
• $k$ is the number of lists

Space complexity: $O(k)$

• For the heap

Note: if you see in here, we need to also push in id() because for heapq if the first element is the same, it will start to compare the second element.

Another way to solve this is to use the index pointer to access the head instead:

class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        minHeap = []
        mergedHead = ListNode()

        for index, head in enumerate(lists):
            if not head: continue
            heapq.heappush(minHeap, (head.val, index))
        
        currHead = mergedHead

        while minHeap:
            minValue, index = heapq.heappop(minHeap)

            currHead.next = lists[index]
            currHead = currHead.next

            lists[index] = lists[index].next
            if lists[index]:
                heapq.heappush(minHeap, (lists[index].val, index))
        
        return mergedHead.next