Top K Elements

Also see Heap Python

N-th largest element in the array

Intuition

To use nth largest element, the idea is we keep a window of n element and then keep moving that window until we reach to the last element inside the array (See Sliding Windows)

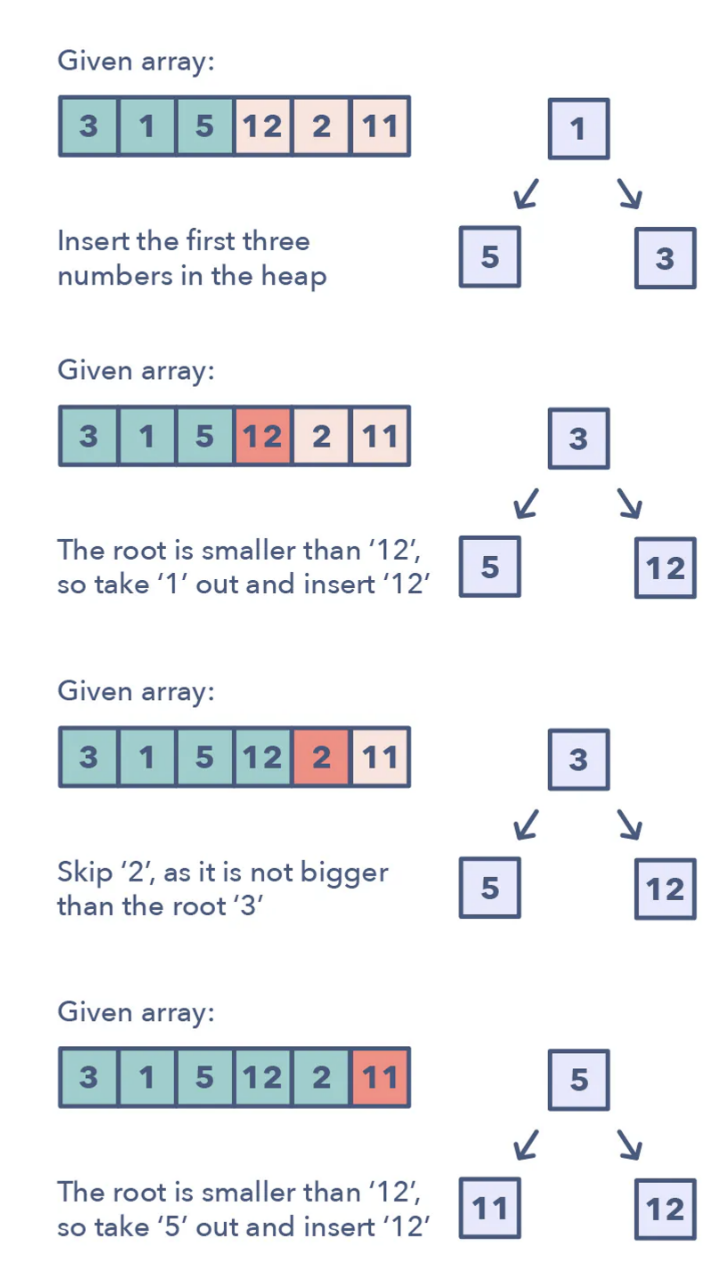
We could code as the following. We compare with the lowest number of the heap by getting heap[0] and use heappushpop() to push an item and also pop 1 out from the heap

def nthLargestInArray(arr, n):
    heap = []
    for i in range(n):
        # We push positive as we want to smallest number in the group of n largest number
        heappush(heap, arr[i])

    for j in range(i + 1, len(arr)):
        # if we find something larger than the smallest number in the group, we put that number in
        if heap[0] <= arr[j]:
            heappushpop(heap, arr[j])

    return heappop(heap)

Optimisation

If you see in here, we actually don't even need to compare if we use heappop() to remove the smallest one for us

For example:

def nthLargestInArray(arr, n):
    heap = []
    for num in arr:
        heappush(heap, num)
        if len(heap) > n:
            heappop(heap)

    return heappop(heap)

Note: in any of our return, it could be better to just return straight heap[0] to avoid calculation in function heappop(num)

N-th smallest element in array

Similar concept

def nthSmallestInArray(arr, n):
    heap = []
    for num in arr:
        heappush(heap, -num)
        if len(heap) > n:
            heappop(heap)
    return -heappop(heap)

Time Complexity

• $O(logn)$ to build a heap, building n elements take $O(nlogn)$

Note

[!note]
For both nthSmallestInArray and nthLargestInArray, the top element will be the nthSmallestInArray (largest within the heap of n elements) and nthLargestInArray (smallest element in the heap of n elements) respectively.

Therefore we have to think of a way to keep this element on the top.

---

If we want nthSmallestInArray, we need to pop out the larger element (because for heapq it will always pop the smaller) — therefore we push in negative

If we want nthLargestInArray, we need to pop out the smaller element (default heapq) so we just push in the positive