Non Overlapping Intervals

Question

Given an array of intervals intervals where intervals[i] = [start_i, end_i], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.

Note: Intervals are non-overlapping even if they have a common point. For example, [1, 3] and [2, 4] are overlapping, but [1, 2] and [2, 3] are non-overlapping.

Example 1:

Input: intervals = [[1,2],[2,4],[1,4]]
Output: 1

Explanation: After [1,4] is removed, the rest of the intervals are non-overlapping.

Example 2:

Input: intervals = [[1,2],[2,4]]

Output: 2

Solution

This is a question where we can apply greedy. Imagine you have the following intervals:

The first thing that we can do is to sort these intervals based on the start number. Otherwise it's hard to be able to know which one came first, which one came second.

Once sorted, you will have something like this:

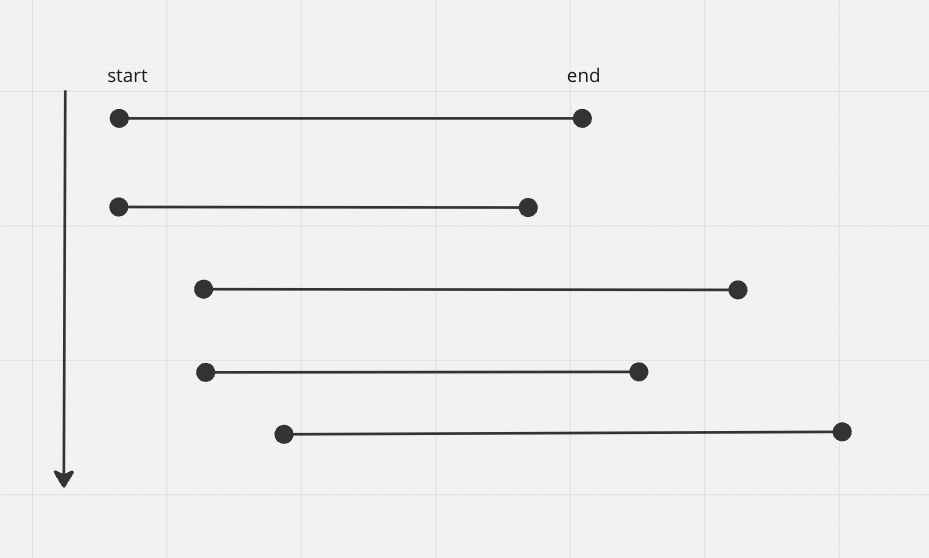
Imagine this will be our array, sorted from the order increasing (display vertically).

All the intervals with smaller start will be first, doesn't matter the end.

When we go through these intervals, we will then need to select a strategy to pick which one.

For example, when comparing this one:

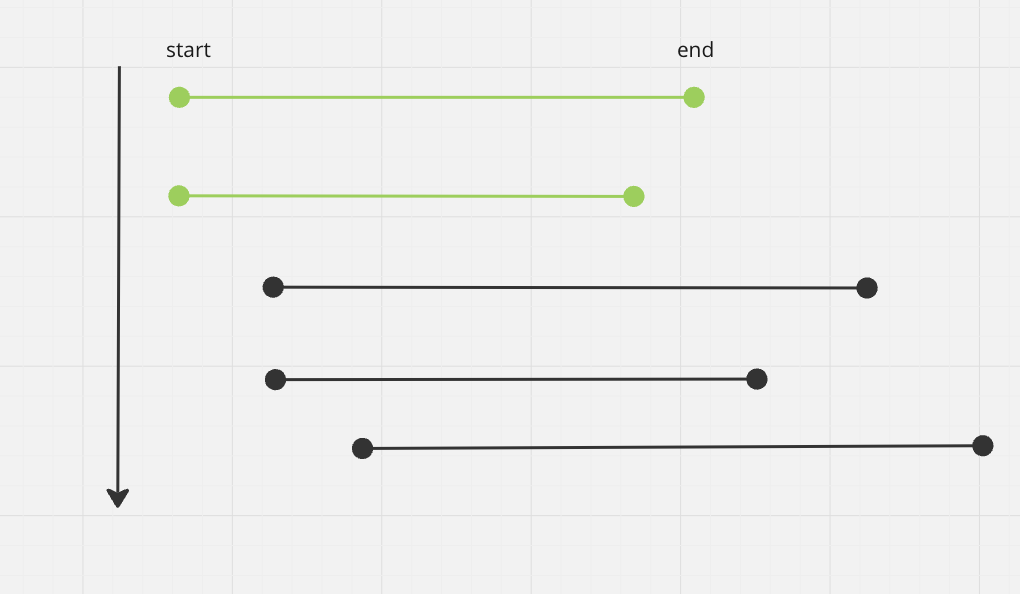
We will prioritise the one with lower end first because it can fits more interval in.

Imagine if we have something like this:

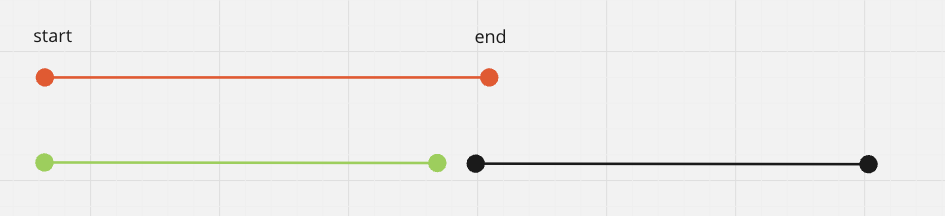
Chosing the red one would not work because it overlap. Since the question is asking for minimum number,

So:

• If it's overlap with the previous interval, we choose the one with lower end
• Else, we keep going and keep track of new previous interval

Implementation

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        intervals.sort(key = lambda x: x[0])

        lastInterval = None
        numberOfNotMergable = 0
        
        for interval in intervals:
            if not lastInterval:
                lastInterval = interval
                continue
            
            if self.overlap(interval, lastInterval):
                numberOfNotMergable += 1
                lastInterval = self.pick(interval, lastInterval)
            else:
                lastInterval = interval
        
        return numberOfNotMergable

    def overlap(self, interval, mergedInterval):
        if not interval or not mergedInterval: return False
        
        startA, endA = interval
        startB, endB = mergedInterval
        
        return not (startA >= endB or startB >= endA) 

    def pick(self, interval, lastInterval):
        startA, endA = interval
        startB, endB = lastInterval
        
        if endB < endA: return lastInterval
        return interval

Time complexity: $O(nlogn + n)$
Space complexity: $O(1)$

Note: in the overlap algorithm here, We consider the case that if startA == endB it's not overlap as of the condition from the question.

For example these intervals are valid: [3,5][5,7]