Maximum Product Subarray

Given an integer array nums, find a subarray that has the largest product, and return the product.

The test cases are generated so that the answer will fit in a 32-bit integer.

Example 1:

Input: nums = [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

Example 2:

Input: nums = [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.j

Intuition

To find the max product in an all postive case, we can simply multiply by the previous result. For example:

[5,1,3,2,9]
Max product = 5 * 1 * 3 * 2 * 9

However in the case where we have negative, it's different:

[2,-5, -2, -4, 3]
Max product: 3 * -4 * -2 = 24

As a result, we need to ignore the 2, -5, -2 which leads to 20

To solve this, we can simply adapt a 2-D dynamic programming pattern

2-D dynamic programming

We start by building a 2D dynamic programming array store all the possible combination:

At 1 point, we can start calculating the product starting at that point. For example, consider we have a subarray of size 2, we have:

Now we can see that the max will be 10. Similarly for size 3, we have:

Now we can see that the max size is 24. Continue on for size 4 we have:

And for size 5 we have

Therefore as we have traverse all the possible subarray, our result is 24.

Implementation

class App2D:
    def maxProduct(self, nums: List[int]):
        dp = [[0 for _ in range(len(nums))] for _ in range(len(nums))]

        maxAmount = self.initialise(dp, nums)
        
        for length in range(2, len(nums) + 1):
            start = 0
            end = start + length - 1

            while (end < len(nums)):
                dp[start][end] = nums[end] * dp[start][end - 1]
                maxAmount = max(maxAmount, dp[start][end])

                start += 1
                end += 1
        
        return maxAmount

    def initialise(self, dp: List[List[int]], nums: List[int]):
        maxAmount = nums[0]

        for i in range(len(nums)):
            dp[i][i] = nums[i]
            maxAmount = max(maxAmount, nums[i])
        
        return maxAmount

Time complexity: $O(n^2)$
Space complexity: $O(n^2)$

1-D Dynamic programing

For optimisation, we can think of how to reduce it to 1-D dynamic programing.

From the above, we can see that the reason why we we need to consider the subarray is we need to consider the situation where the subarray start at the next number — hence, skipping the current number.

If doing like that, we can also consider something like this:

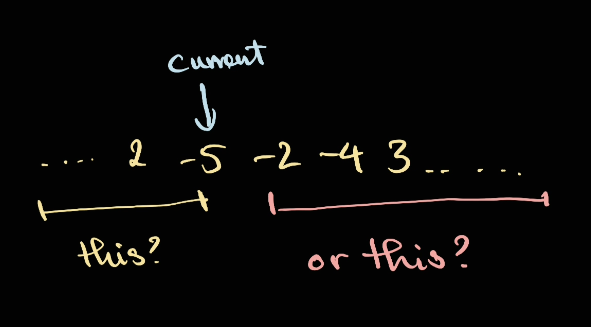
We can take:

• The result of everything before up to the current number:
  • This should give us the maximum result of a sub array counting from the left (including this number)
• The result of everything after the current number:
  • This should give us the maximum result of a sub array counting from the right (excluding this number)

This makes sense because if we look at our 2-D dp table above, the maximum result of -5, -2, 4, 3 has been discovered when skipping -5 and take -2, 4, 3:

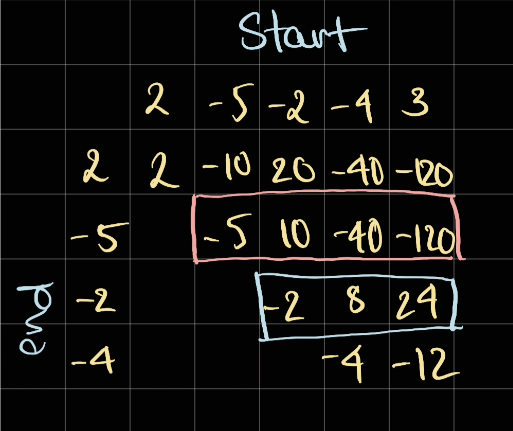
Therefore, we can consider:

1. Start from left -> right and calculate the maximum possible product of all sub-array
2. Start again from right -> left and calculate the maximum product of all sub-array so that we make sure we don't miss anything

Edge cases.

For example there is an edge case if there is a 0 in the middle:

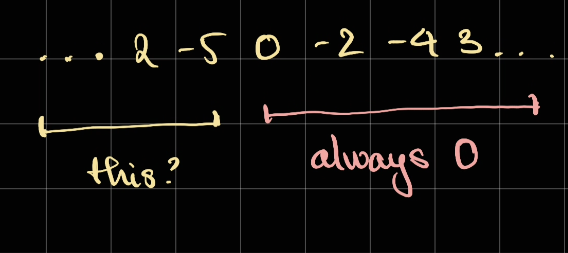
In this case, our right handside is always 0. Hence it will void all the result accumulate from -2, -4, 3. Therefore, we should skip 0 and only consider it to stand by itself without combining with other numbers.

Implementation

class App:
    def maxProduct(self, nums: List[int]):
        maxAmount = nums[0]

        amount = 1
        # Go from left -> right
        for i in range(0, len(nums)):
            if nums[i] == 0:
                maxAmount = max(nums[i], maxAmount)
                amount = 1
                continue
            amount *= nums[i]
            maxAmount = max(maxAmount, amount, nums[i])

        amount = 1
        # Go from right -> left 
        for i in range(len(nums) - 1, -1, -1):
            if nums[i] == 0:
                maxAmount = max(nums[i], maxAmount)
                amount = 1
                continue
            amount *= nums[i]
            maxAmount = max(maxAmount, amount, nums[i])

        return maxAmount

Time complexity: $O(n)$
Space complexity: $O(1)$