Palindrome Partitioning

Question

Given a string s, partition s such that every substring of the partition is a  palindrome. Return all possible palindrome partitioning of s.

Example 1

Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]

Example 2:

Input: s = "a"
Output: [["a"]]

Intuition

For this question, it's pretty hard as the pattern needs to be modified a bit from other regular backtracking.

For example, consider the string aabd. We know that our base case should be:

• a,a,b,d

So that give us a hint of a for loop from 0 -> len(s) to start. And then we just have to follow this branch out tree:

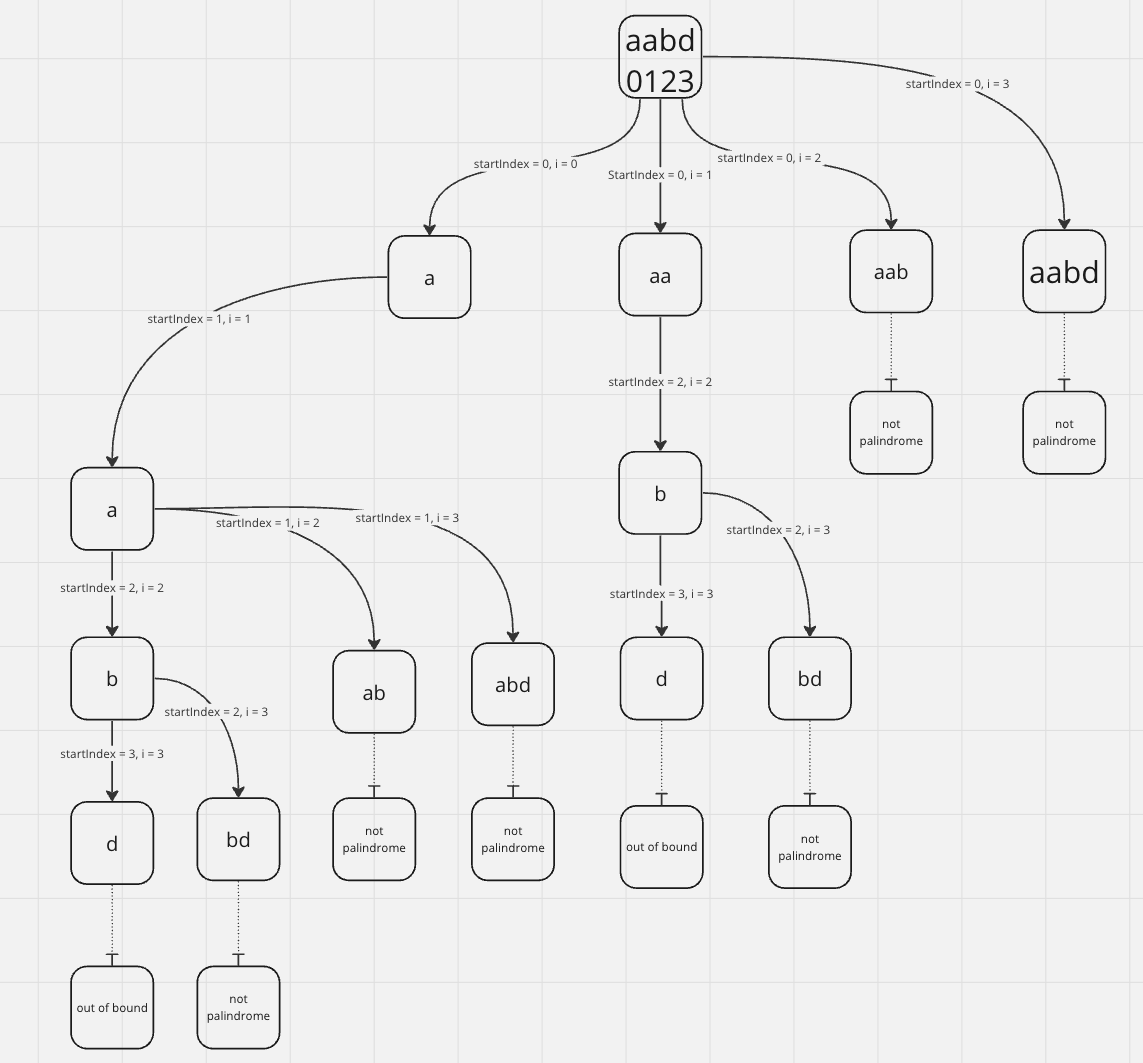
So if it's a palindrome, we going to explore, otherwise, we don't and stop.

Implementation

class App:
    def partition(self, s: str) -> List[List[str]]:
        self.result = []
        self._partition(0, s, [])
        return self.result
    
    def _partition(self, startIndex: int, s: str, tmp) -> None:
        if startIndex >= len(s):
            self.result.append(tmp.copy())
            return
        
        for i in range(startIndex, len(s)):
            if self.isPalindrome(s, startIndex, i):
                tmp.append(s[startIndex : i + 1])
                self._partition(i + 1, s, tmp)
                tmp.pop()
    
    
    def isPalindrome(self, s, start, end):
        while (start < end):
            if (s[start] != s[end]): return False
            start += 1
            end -= 1
        
        return True

Time complexity: $O(n^2 \times 2^n)$

• We have $n$ length in a string. We have to loop through it: $O(n)$
• For each substring, we need to check for isPalindrome, worst case is $O(n)$
  • So the two above combined in the for loop is $O(n^2)$
• Each one, we need to go through a choose or not choose for n length, therefore it's $O(2^n)$

Space complexity: $O(w \times n)$

• w is the average length of temporary list