N-Queens

Question

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Solution

Intuition

To solve this question, we should go row by row trying to place the queen at each row.

If we can place n queens at n rows, that means there should be at least 1 queen at a row.

So we can do something like this:

Given this board, we can put a Queen Q at any position in the board. Let's go row by row.

At the first row, we choose the put the queen at the first position.

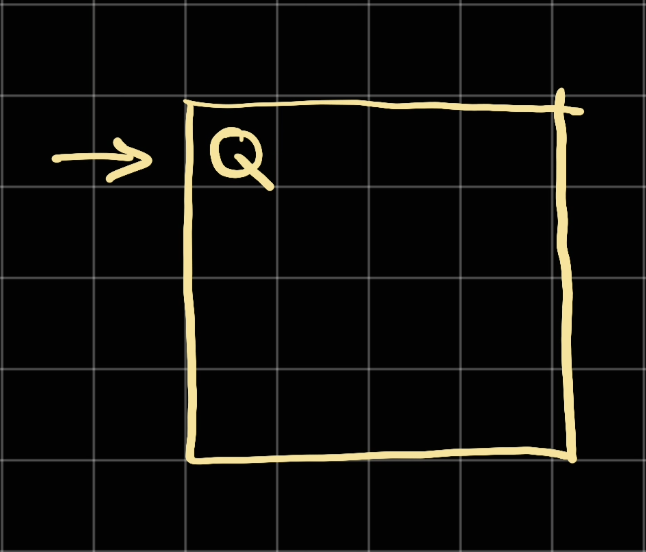
This will cross out a few rows available for us base on chess rules:

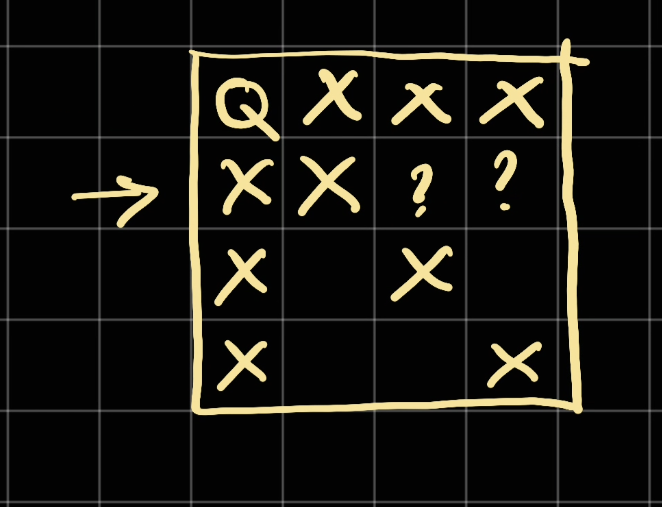
The marker x is what crossed out and can't place a queen there. Now at row = 1, we only have 2 positions.

We try one of them:

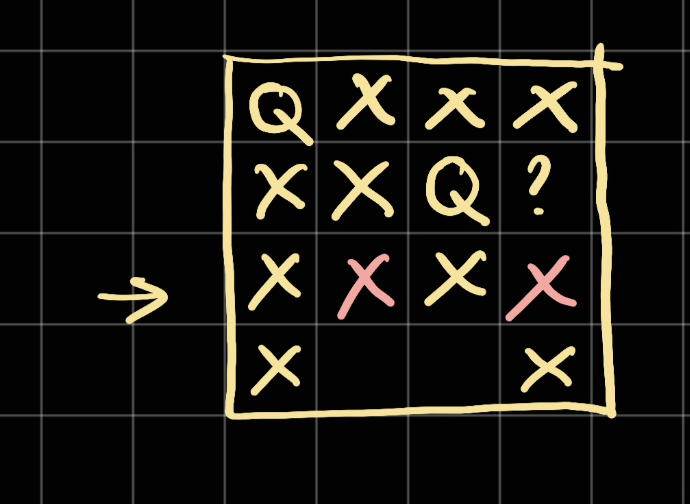
This will give us no option at row = 1. Therefore, we go back to the previous row and try the other position:

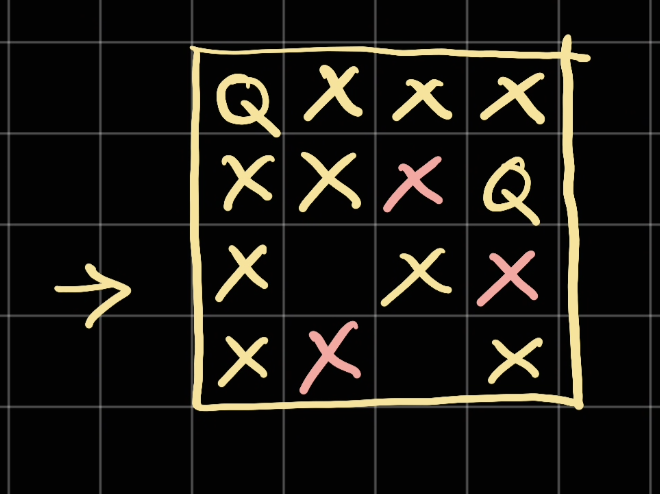
This will give us a position to go at row = 2, We can place a Q there.

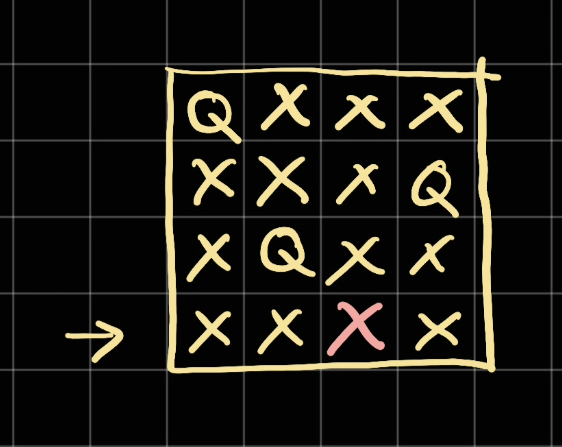
Now at this row, we don't have any available position left to go. Therefore, we have to undo our moves and then start at the next Q from row = 0:

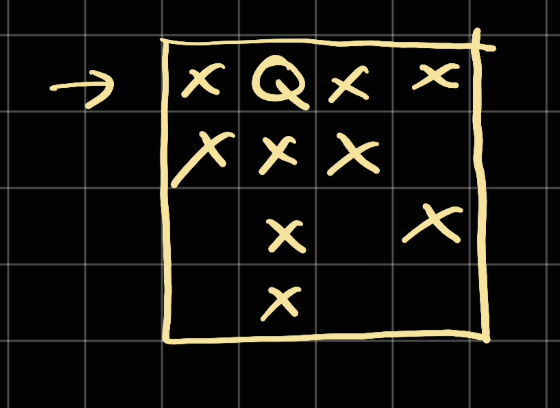
We continue our algorithm to check the next rows.

Quick way to mark unavailable position

Consider this following position:

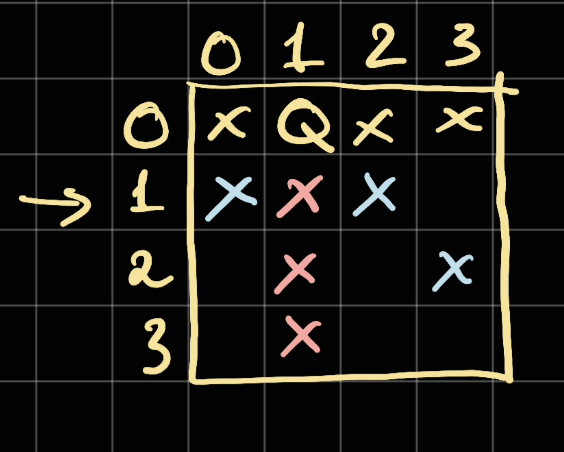
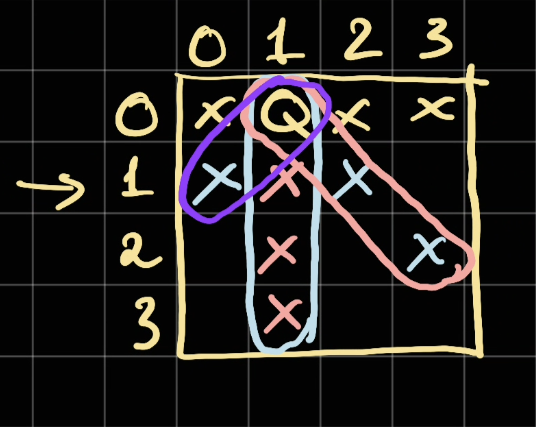
Imagine after marking our queen Q at (0, 1). We have to keep track of:

1. The unavailable column: column 1
2. The unavailable backwardDiagonal (\) : (1,2), (2,3)
3. The unavailable forwardDiagonal (/): (1, 0)

[!note]
We don't have to consider the unavailable row because we always moving to the next row after placing a queen. There is no reason to try out the current row

The column is simple, it's just the col of the placement, in this case will be 1.

For the backwardDiagonal (\ — the pink diagonal group), notice that all the positions in that group always follow the same formular:

$$col - row = 1$$

For example:

• Position (0, 1): 1 - 0 = 1
• Position (1, 2): 2 - 1 = 1
• Position (2, 3): 3 - 2 = 1

For the forwardDiagonal (/ — the purple diagonal group), notice that all the positions in that group always follow this formular:

$$row + col = 1$$

For example:

• Position (0, 1): 0 + 1 = 1
• Position (1, 0): 1 + 0 = 1

As a result, to keep track of these diagonal, we can just store col - row and row + col of the current marker Q

Implementation

class App:
    EMPTY = "."
    QUEEN = "Q"

    def __init__(self):
        self.result = []
        self.occupiedColumn = set()
        self.occupiedForwardDiagonal = set() # (row + col)
        self.occupiedBackwardDiagonal = set() # (col - row)
        
    def solveNQueens(self, n):
        board = [[App.EMPTY for i in range(n)] for j in range(n)]
        self.placeQueen(board, 0)
        return self.result

    
    def placeQueen(self, board: List[List[str]], row: int):
        if (row >= len(board)): 
            self.result.append(self.convertBoardToResult(board))
            return
        
        for col in range(len(board[0])):
            if self.canPlaceQueen(row, col):
                board[row][col] = App.QUEEN
                self.occupiedColumn.add(col)
                self.occupiedBackwardDiagonal.add(col - row)
                self.occupiedForwardDiagonal.add(row + col)
                
                self.placeQueen(board, row + 1)
                
                board[row][col] = App.EMPTY
                self.occupiedColumn.remove(col)
                self.occupiedBackwardDiagonal.remove(col - row)
                self.occupiedForwardDiagonal.remove(row + col)

    def canPlaceQueen(self, row: int, col: int) -> bool:
        isOccupied = col in self.occupiedColumn or (col - row) in self.occupiedBackwardDiagonal or (row + col) in self.occupiedForwardDiagonal
        return not isOccupied

    def convertBoardToResult(self, board: List[List[str]]) -> List[str]:
        result = []
        
        for row in board:
            result.append("".join(row))
        
        return result

Time complexity: $O(n^2)$
Space complexity: $O(n^2)$