Design Consistent Hashing

Rehashing problem

Rehashing has a problem is that adding or removing 1 element can affect other unwanted elements result.

For example if we have 4 servers and following the hash as follows:
$$ serverIndex = hash(key) % 4 $$
Given this following keys:

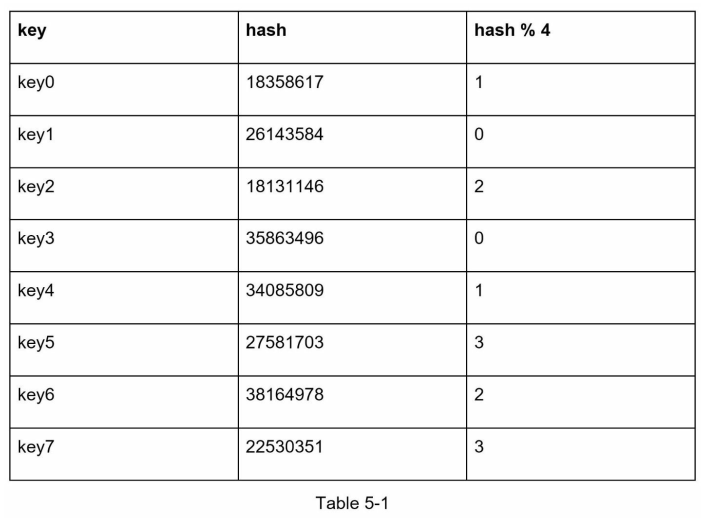
We have the following hash result:

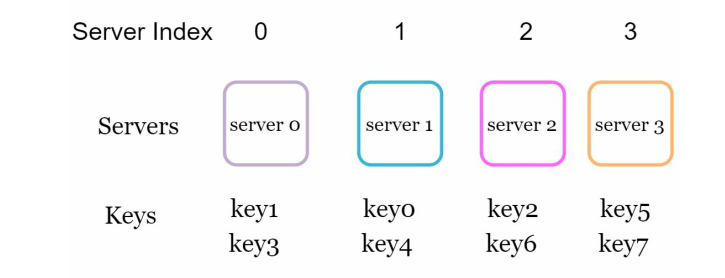
So when key2 talks to our server, it should map to server2

The problem

The problem comes when we removing 1 server. Supposed that server1 goes offline. We only have 3 servers. Therefore the hash algorithm changes to:
$$ serverIndex = hash(key) %3 $$
However, this changes all the server distribution.

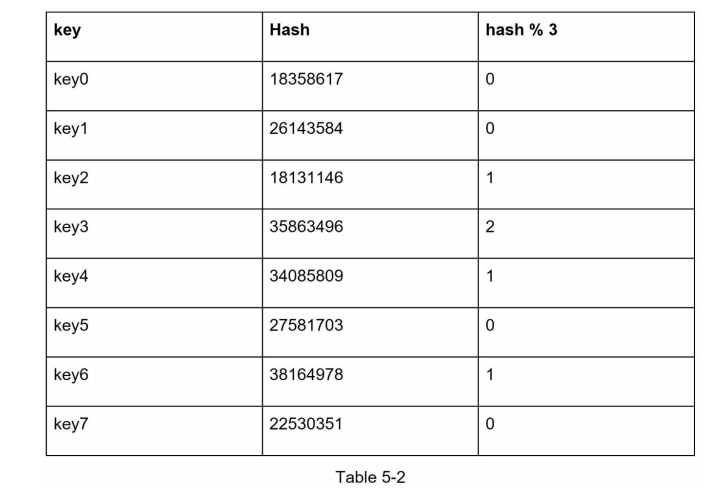
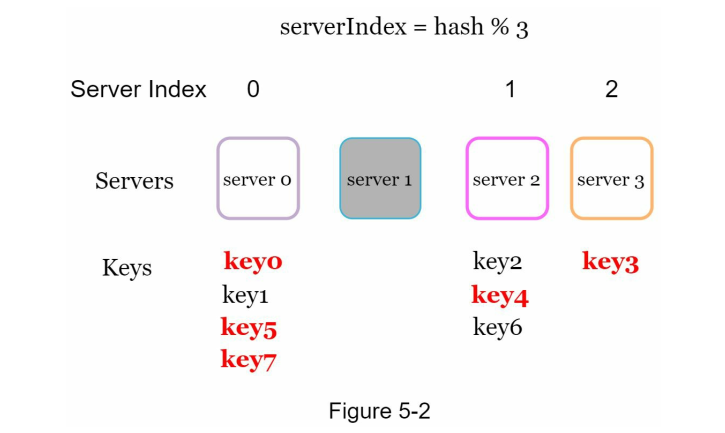
In reality, when server1 offline, only traffic from server1 should be migrate to the other server, the other servers traffic should stay the same

Consistent hashing algorithm

Supposed that we use SHA1 hashing algorithm with value range goes from $0$ to $2^{260} - 1$. We have $n$ spaces from $x^0$ to $x^{n}$ with $n = 2^{260} - 1$.

We connect the 2 ends, it creates a circle:

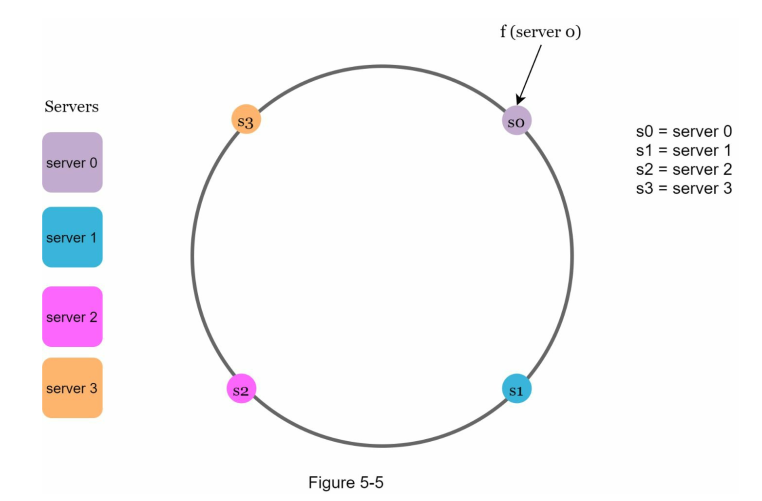
Assinging the servers

We can use the same hash function (SHA1) $f$ to map the server to the ring.

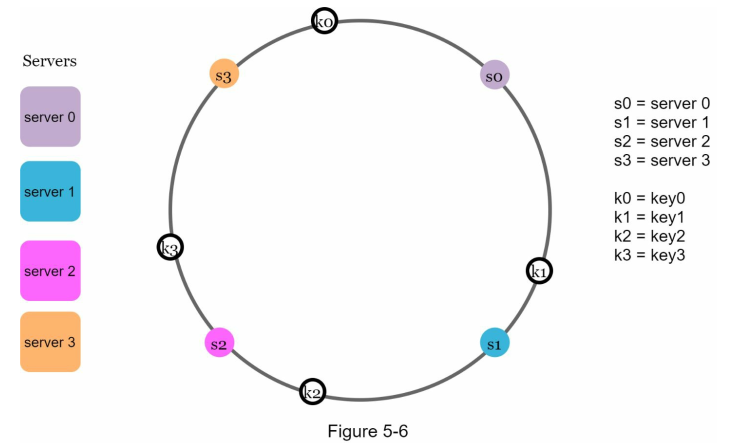
Assigning the keys

We can assign the keys using the same hash function.

Server lookup

To identify which keys belong to which server, we go clockwise:

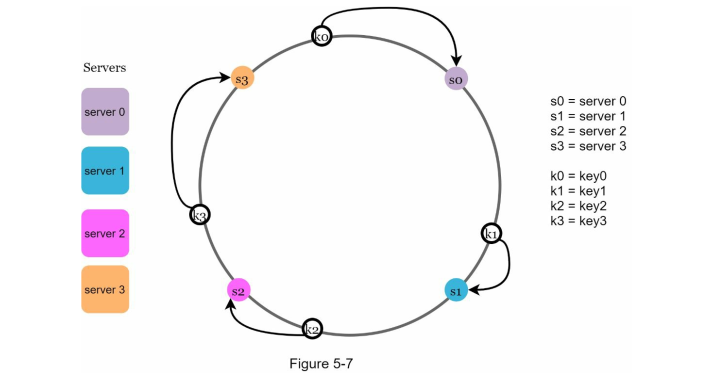
For example if we're at k0, our server would be s0.

Add a server

Let's say between s3 and s0 we want to add s4.

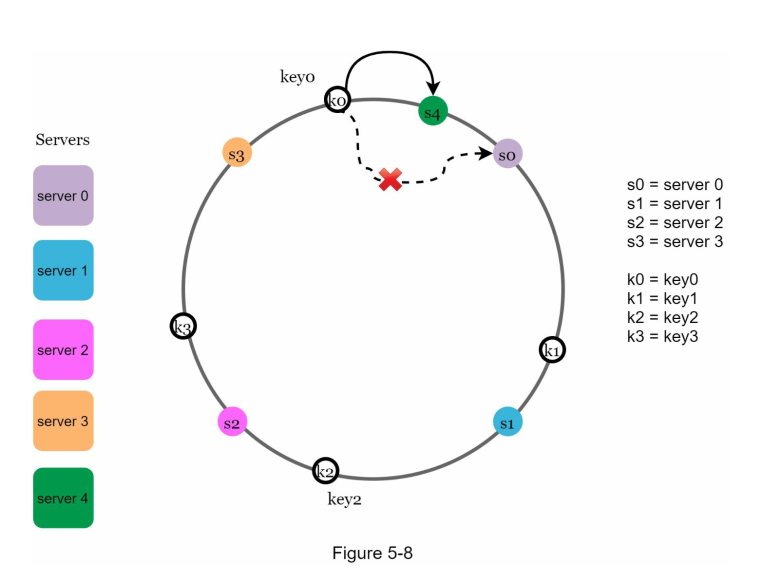
As a result, only k0 needs to be redistributed. k1, k2, and k3 stays the same.

Affected keys

To find which keys are going to be affected, we:

1. Start from the newly added server
2. Move anticlockwise until another server is found
3. The keys in between are affected keys.

In this example, we start with s4. Moving anticlockwise until we see s3. As a result, only k0 is affected and needed to be redistributed.

Removing a server

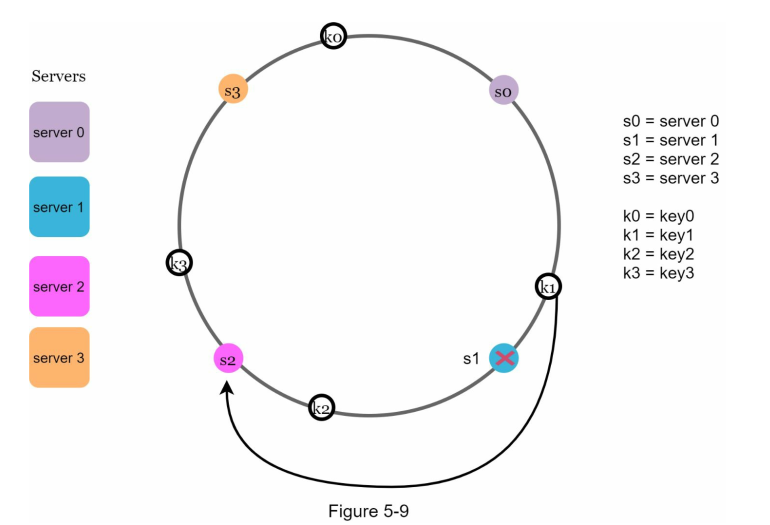
Similarly, let's say we remove s1, we only need to map k1 to s2

Affected keys

It's the same steps as the above:

1. Start from the newly added server
2. Move anticlockwise until another server is found
3. The keys in between are affected keys.

So in here, since s1 is removed, we move aniclockwise and find s0. Since from s0 to s1 we have k1. Only k1 is affected, we redistribute k1.

Problem with basic approach

Because we have no control on where to put the server, we run into 2 possible problem:

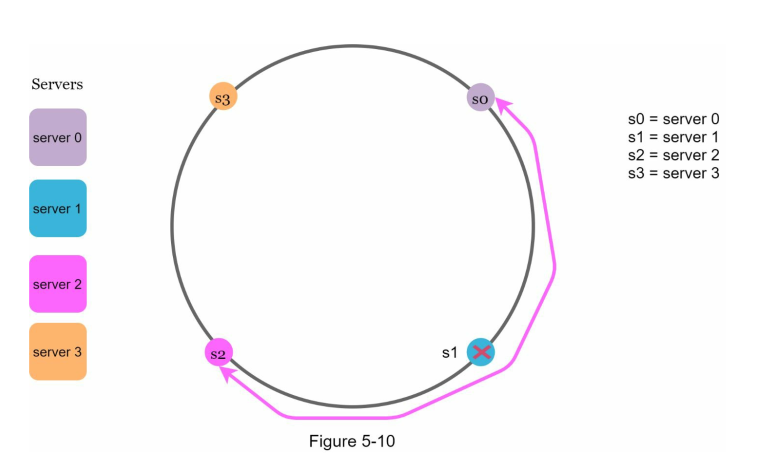
• The gap 1 particular server is too big:
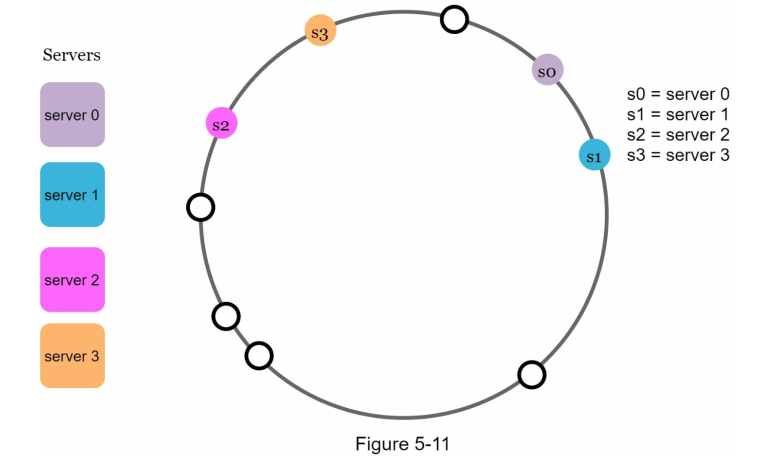
• The keys are not distributed uniformly between places which might cause some server doesn't have any keys:

Solution: Virtual node

Virtual node holds reference to the real node. 1 real node can be represented by many virutal nodes spread out across the ring.

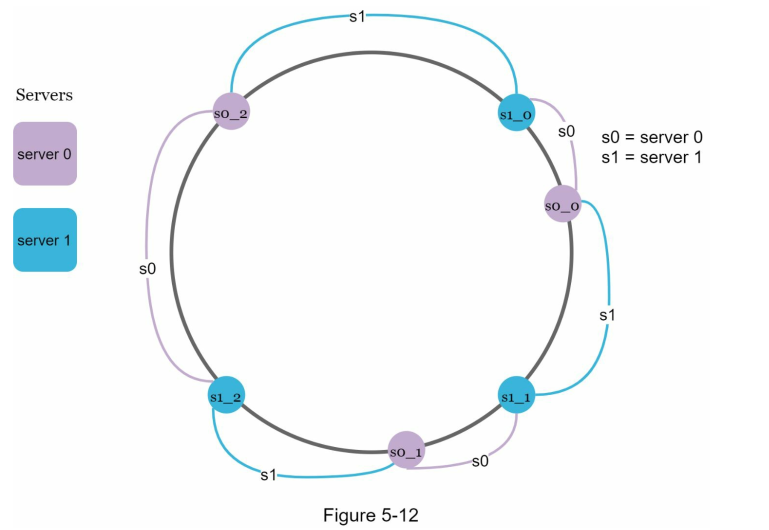
So in this example, s0 has s0_0, s0_1, s0_2 and s1 has s1_0, s1_1, s1_2

When a node is added to a place, if it goes to the virtual node, it will be assigned to its corresponding server:

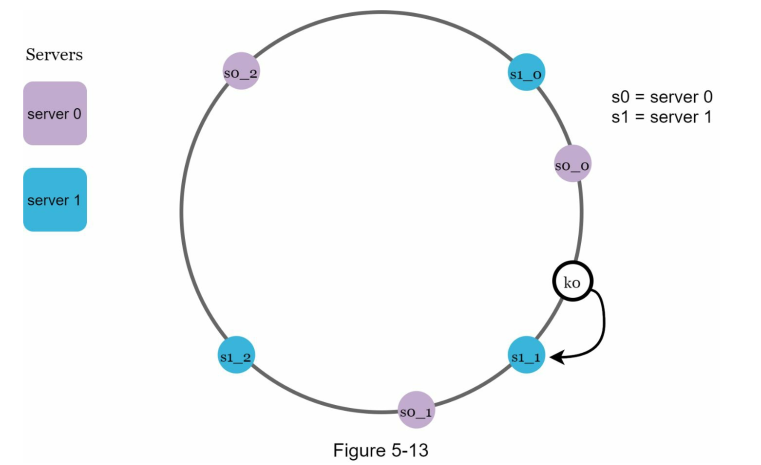
For example, k0 will be assigned to server1.

Why this work?

This is because as he number of virtual nodes increase, the distribution keys becomes more balanced. The standard deviation gets smaller the more virtual node added.

Trade off

The more virtual nodes, the more space we need in our system.