Subtree Of Another Tree

Question

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

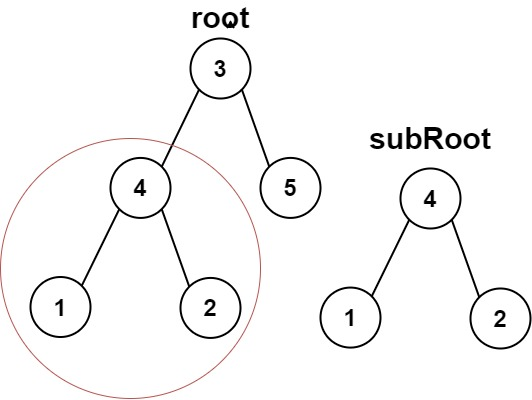
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

Example 2:

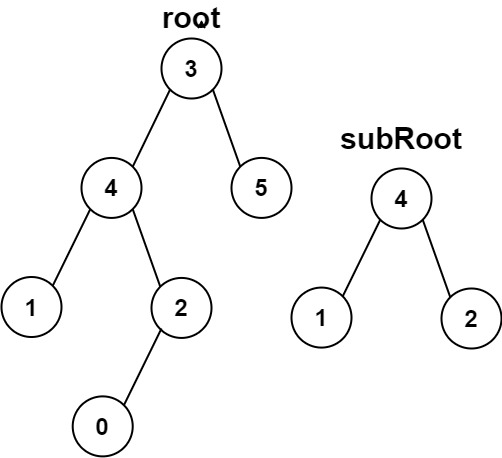
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

Solution

For this, we need 2 recursions call because for each node at the tree, we need to go through another check of Same Tree.

Implentation

class App:
    def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if not root and not subRoot: return True
        if not root or not subRoot: return False

        if self.isSameTree(root, subRoot): 
            return True
        
        return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
    

    def isSameTree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
        if not root and not subRoot: return True
        if not root or not subRoot: return False

        if root.val != subRoot.val: 
            return False

        return self.isSameTree(root.left, subRoot.left) and self.isSameTree(root.right, subRoot.right)

Time complexity: $O(nk)$

• $n$: number of nodes in the root tree
• $k$ number of nodes in the subRoot tree

Space complexity: $O(logn \times logk)$ — Recursion heap

• $logn$ — height of the root tree
• $logk$ — height of the subRoot