Floyd's Loop Detection

Problem:

• Given a looped linkedlist, try to find the start node of the looped linked list

Algorithms

• If we have 2 pointers, fast pointer moves twice as fast as slow.
• We can then prove that x == z as following

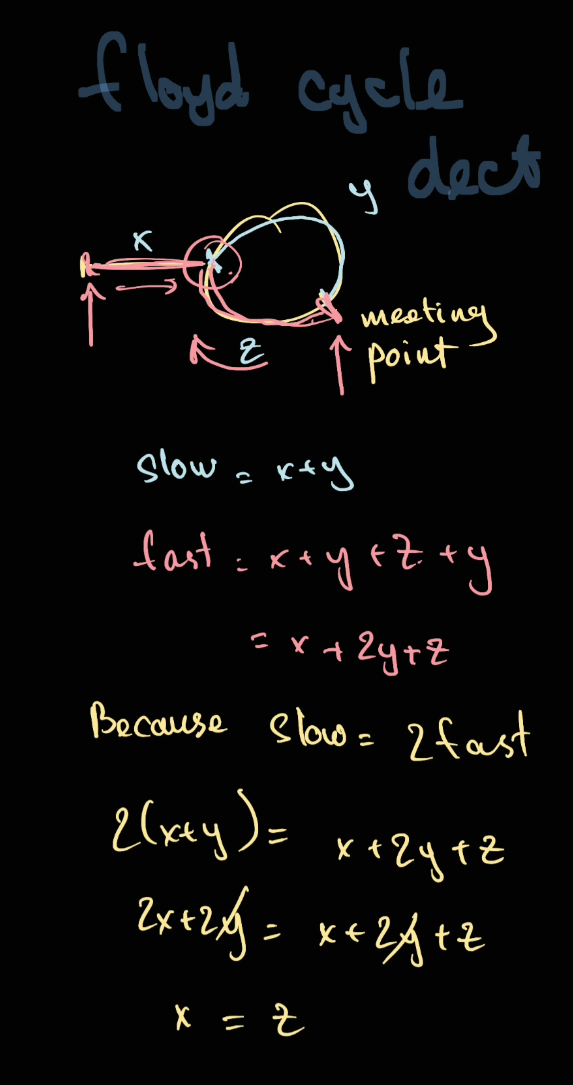
Because of that, if we put a pointer at the start, and a pointer at the meeting point. And keep increasing those pointers.

We're going to meet in between.

[!note]
These pointers fast and slow needs to start from the same point at the start.

So we have fast = node and slow = node.

NOT fast = node.next and slow = node.next in contrast to Find half of a linked list

Time Complexity:

• $O(n - l)$
• where $n$ is the number of nodes and $l$ is the length of the loop

Example

from typing import *

import unittest

class Node:
    self.val: int
    self.next: 'Node'

    def __init__(self, val: int):
        self.next = None
        self.val = val

class App:
    def circularDetection(self, node: 'Node'):
        slow, fast = node, node

        while (fast and fast.next):
            fast = fast.next.next
            slow = slow.next

            if fast == slow:
                break
        else:
            return None
        
        slow = node

        while (slow != fast):
            slow = slow.next
            fast = fast.next
        
        return slow.val

    

class AppTest(unittest.TestCase):
    def setUp(self):
        self.app = App()
        return super().setUp()
    
    def test_givenCircularLinkedList_shouldDetect(self):
        root = Node(1)
        root.next = Node(2)
        root.next.next = Node(3)
        root.next.next.next = Node(4)
        root.next.next.next.next = Node(5)
        root.next.next.next.next.next = Node(6)
        root.next.next.next.next.next.next = Node(7)
        root.next.next.next.next.next.next.next = root.next.next

        actual = self.app.circularDetection(root)
        self.assertEqual(actual, 3)

if __name__ == "__main__":
    unittest.main()

[!note]
For floyd loop detection, we need to have fast and slow start at the same start point.