Container With Most Water

Question

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Example

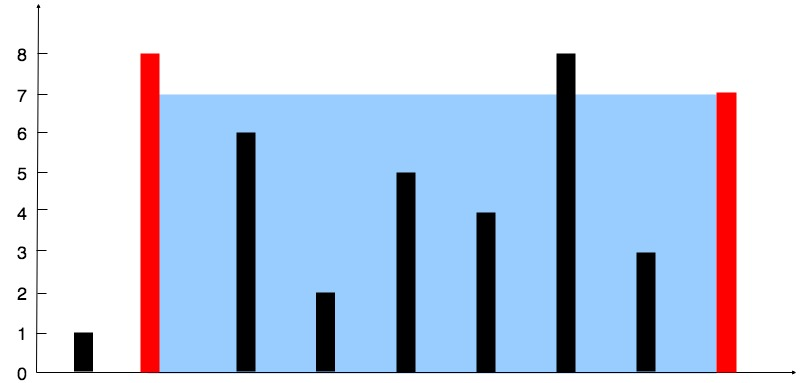
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Input: height = [1,1]
Output: 1

Solution

Using Two pointers, the trick in here is we start from left and right.

An area is calculated as below:

$$ Area = height \times width$$
For maximum Area, we need to maximise the height and maximise the width.

If we have left and right at the 2 ends of the array, we have the maximised width:

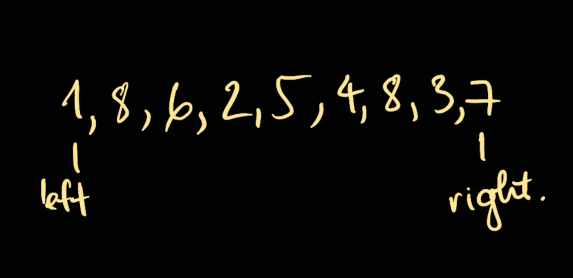
As a result, we want to find the maximised height. However, in trade of for maximising height, we losing our width.

Therefore, it makes sense to find the new height for the smaller height.

In the example above, we want to move left because height[left] < height[right].

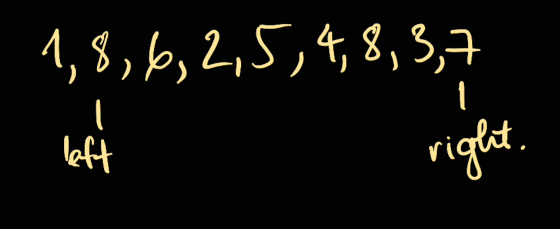
Now we want to move right as height[right] < height[left].

The idea is as we sacrificing our width anyways, we want to maximise height

Implementation

class App:
    def maxArea(self, height: List[int]) -> int:
        if len(height) < 2: raise Exception("Illegal arugments")
        
        maxArea = 0
        left, right = 0, len(height) - 1
        
        while (left < right):
            area = min(height[left], height[right]) * (right - left)
            maxArea = max(area, maxArea)
            
            # we move whichever one is smaller to find the next max
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1
        
        return maxArea

Time complexity: $O(n)$
Space complexity: $O(1)$