Climbing Stairs

For example, climbing stairs: https://leetcode.com/problems/climbing-stairs/

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example:

Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Backtracking

We can follow the backtracking template, therefore have something like this

class App:
    def climbStairs(self, n: int) -> int:
        if n <= 0:
            return 0

        def climb(remain: int = n):
            nonlocal result
            if remain == 0:
                result += 1
                return

            if remain < 0:
                return

            for step in [1, 2]:
                climb(remain - step)

        result = 0
        climb()
        return result

However, using this template there is no way to store the result back into cache (because the result only return back when remain == 0). In order to store back, we need a way to trace back the original root that we used it from.

Topdown DP

To solve topdown DP, we startfrom n steps.

For example

    def climbStairsTopdown(self, n: int) -> int:
        if n == 0: return  0
        cache = {}
        
        def climb(remain: int):
            if (remain == 0): return 1
            
            if (remain < 0): return 0
            
            if remain in cache: return cache[remain]
            
            cache[remain] = climb(remain - 1) + climb(remain - 2)
            
            return cache[remain]
        return climb(n)

In here we can use cache because the result of the sub problem will be return up to its parent. For example if n = 5

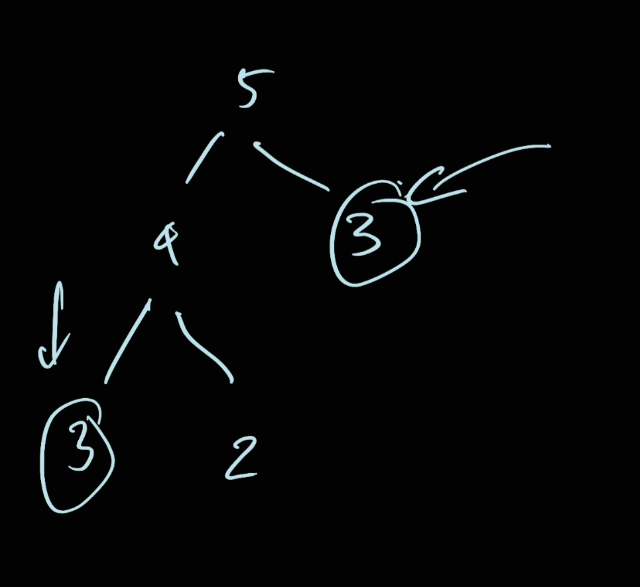
We have 3 in here is already calculated from 5. Because we're using DFS so it will explore either the left or the right of the tree first. Because of that we've already calculated it.

Once we calculated, we can then store in the cache dictionary so that we already have the result of what we did

Bottom Up DP

For DP, you cannot brute force anymore but rather finding a pattern of what we have so far. For example let's consider the following case.

We want to find the number of unique ways to reach to step 3

steps:              1 2 3
numberOfWays:       1 2 _

Let's work from backwards at step 3. At step 3, we know that we can reach by stepping 1 step from step 2. Which means for each way of getting to step 2, we can do +1 to get to step 3.

We know that to reach to step 2, we can either do:

1. 1 step + 1 step
2. 2 step

That means to reach to step 3, we can do

1. 1 step + 1 step + 1 step
2. 2 step + 1 step

So therefore the unique way to get to step 3 from step 2 is 2.

We cal also reach to step 3 from step 1. To reach to step 1 we can do

1. 1 step

From step 1 we know that to reach to step 3, we can only step 2 step

1. 1 step + 2 step

[!important]
We don't count 1 step + 1 step + 1 step here since if we do 1 step, it reaches to step 2 already and therefore overlap with step 2 case

From the above, we know that to reach to step 3 we have:

• 2 ways from step 2
• 1 way from step 1

So we have a total of 3 unique way.

We can then update our steps:

steps:              1 2 3 4
numberOfWays:       1 2 3 _

Similarly, for step 4 we can either do:

• do 1 step for each steps in step 3
• do 2 step for each steps in step 2

Therefore there are 5 unique steps reaches to step 4

Implementation

class App:
    def climbStairs(self, n: int) -> int:
	    if n <= 2: return n
	    
        numberOfWays = [0] * n
        numberOfWays[0] = 1
        numberOfWays[1] = 2

        for i in range(2, n):
            numberOfWays[i] = numberOfWays[i - 1] + numberOfWays[i - 2]
        
        return numberOfWays[n - 1]

Time complexity: $O(n)$ — loop through n elements
Space complexity: $O(n)$ — to store the arrays

Optimisation

As we can see in here, we only need 2 variables to calculate the current ways:

1. Result of 1 step previous n
2. Result of 2 steps previous n

As a result, we can refactor our code to use these 2 variables only

def climbStairs(self, n: int) -> int:
	if n <= 2: return n

	previousStepResult = 1
	currentResult = 2

	for i in range(2, n):
		previous = currentResult
		currentResult += previousStepResult
		previousStepResult = previous
	
	return currentResult

Time complexity: $O(n)$ — loop through n elements
Space complexity: $O(2)$