Subset

Question

Given an integer array nums of unique elements, return all possible subsets (the power set).

The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:

Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2

Input: nums = [0]
Output: [[],[0]]

Solution

https://leetcode.com/problems/subsets/

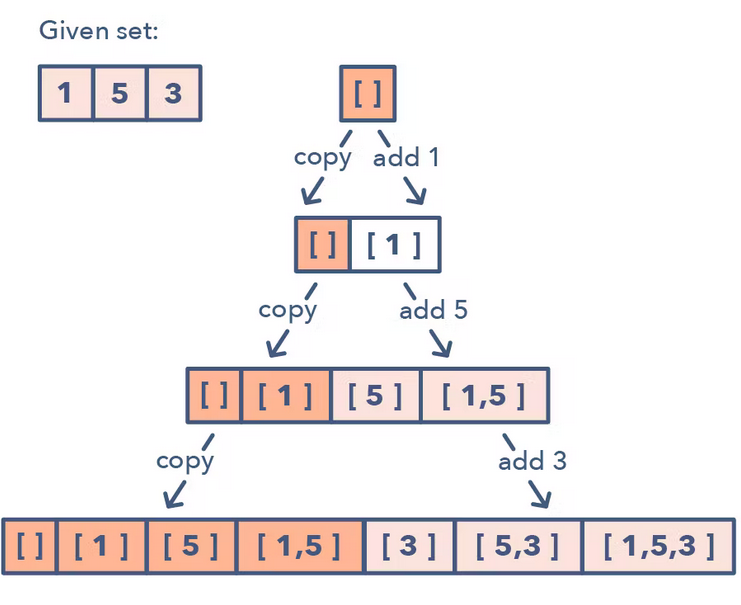
Start with an empty set and keep adding up elements to each of the set while keeping the original set the same

Given a subset of [1,5,3]

1. Start with an empty set:

[[]]

2. Add the first number (1) to all the existing subsets to create a new set:

[[], [1]]

3. Add the second number (5) to all existing subset

[[], [1], [5], [1,5]];

4. Add the third number (3) to all exisiting subset

[[], [1], [5], [1,5], [3], [1,3], [5,3], [1,5,3]]

Ways to identify

• Combination, Permutation
  Time complexity: $O(n \times 2^n)$
• For a given number there are 2 choices (take or not take). So in this case, for example if we have 3 number, we have $2 \times 2 \times 2 = 2^3$ choices. Therefore for $n$ numbers there are $2^n$ possible choice to make a subsets
• Our subsets can be up to $n$ length. After making a subset, you need to copy the previous subset and the worst case has $n$ elements. So it's $n \times 2^n$

Using Bottom-up recursion

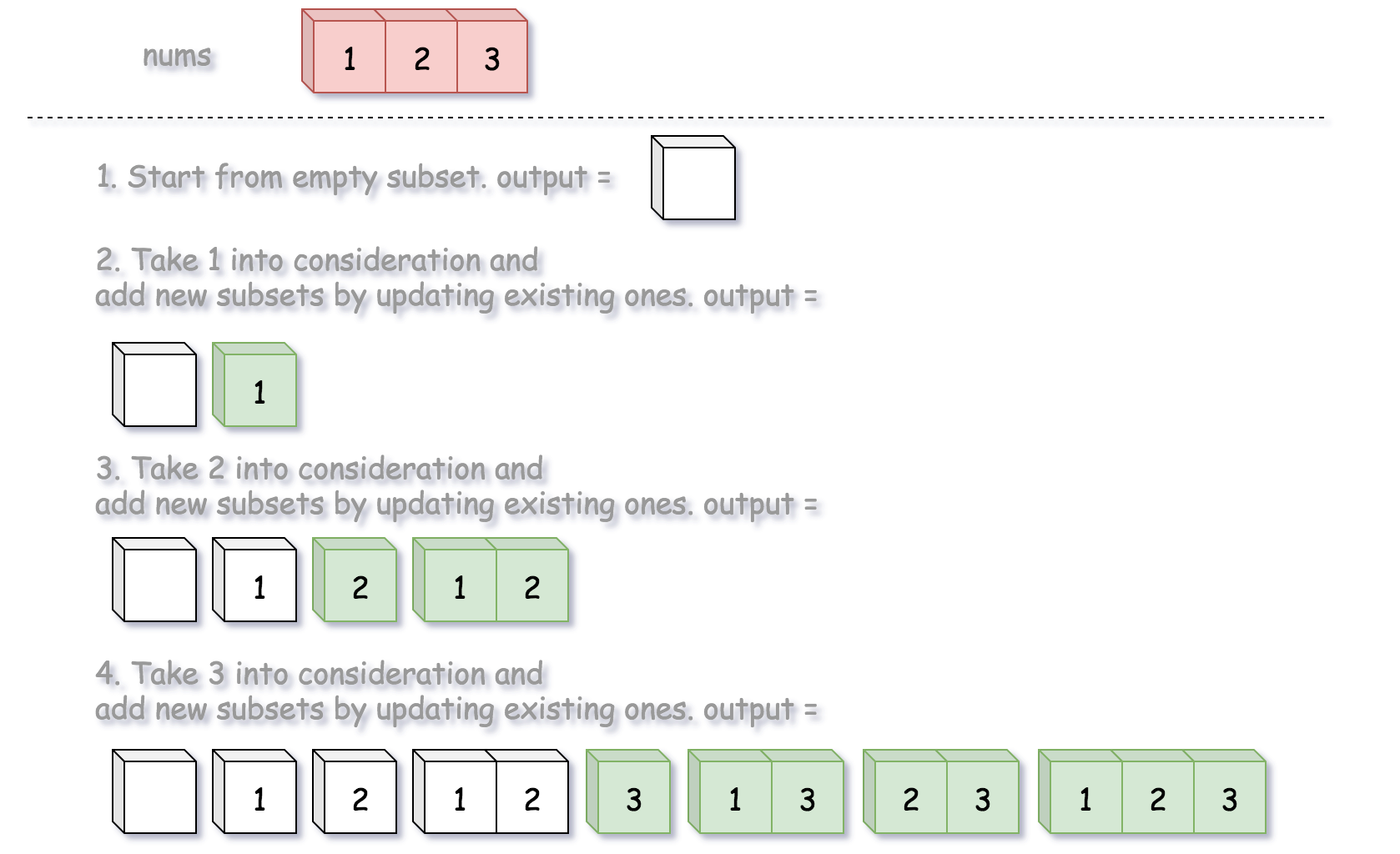
Intuition
Starting with an empty set [[]] and for each number we make a new set from the previous set and add it into the result. The idea is the same as the explaination above

def generateAllSubsets(nums: List[int]) -> List[int]:

    def combine(index: int):
        if index >= len(nums):
            return [[]]

        previousSubsets = combine(index + 1)
        currentSubsets = []

        for i in range(len(previousSubsets)):
            subset = previousSubsets[i].copy()
            subset.append(nums[index])
            currentSubsets.append(subset)

        currentSubsets.extend(previousSubsets)
        return currentSubsets

    return combine(0)

This is more like a BFS as you explore all the number equally

Space complexity: $O(n \times 2^n)$ as big as time space because we need to generate a big enough subset to store all the numbers

Using Back-tracking (Recommended)

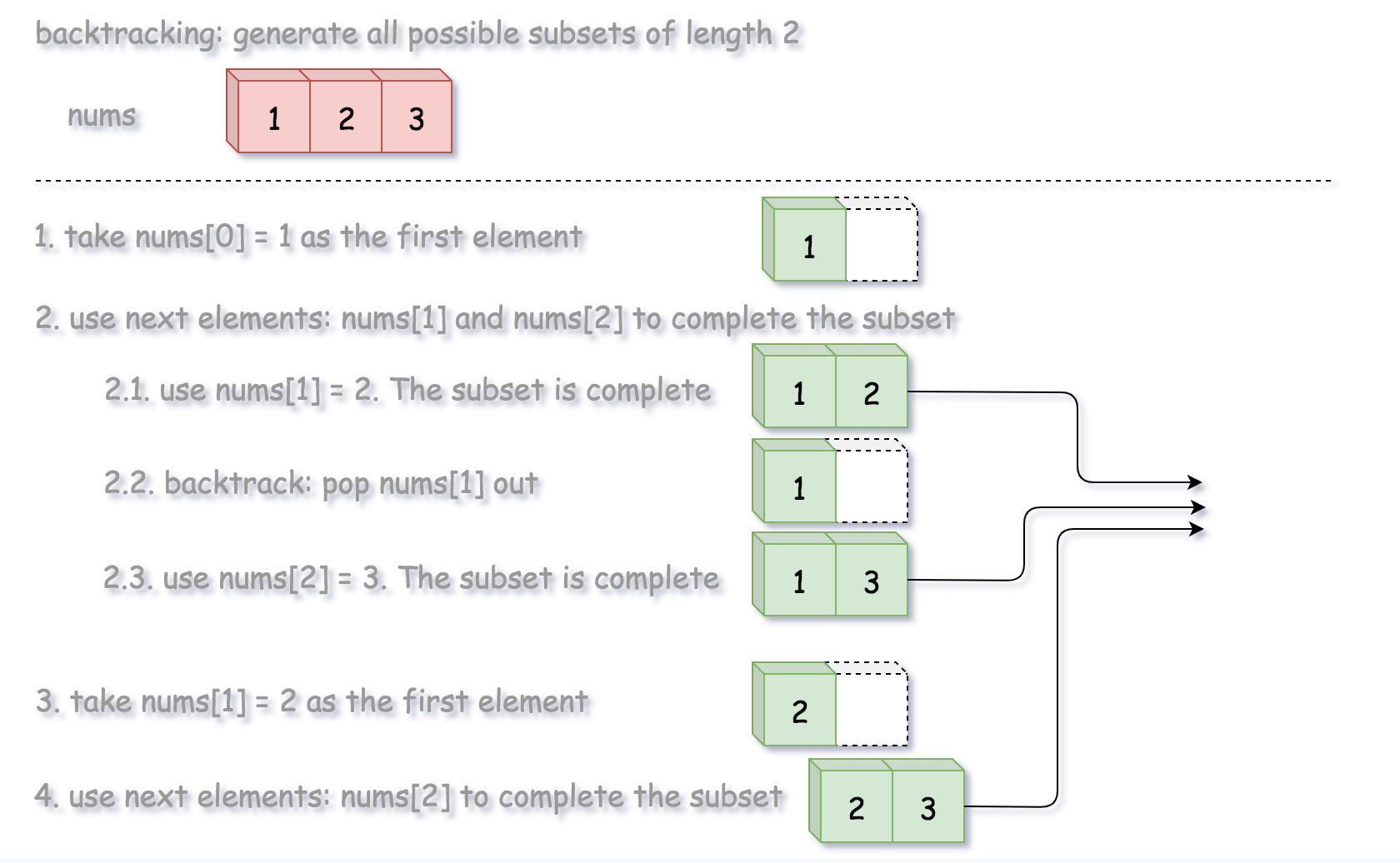
Intuition
Similar to above, start with an empty set [[]]. However this time, we generate all the possible subsets given the inital number, for example

Space Complexity: $O(n)$

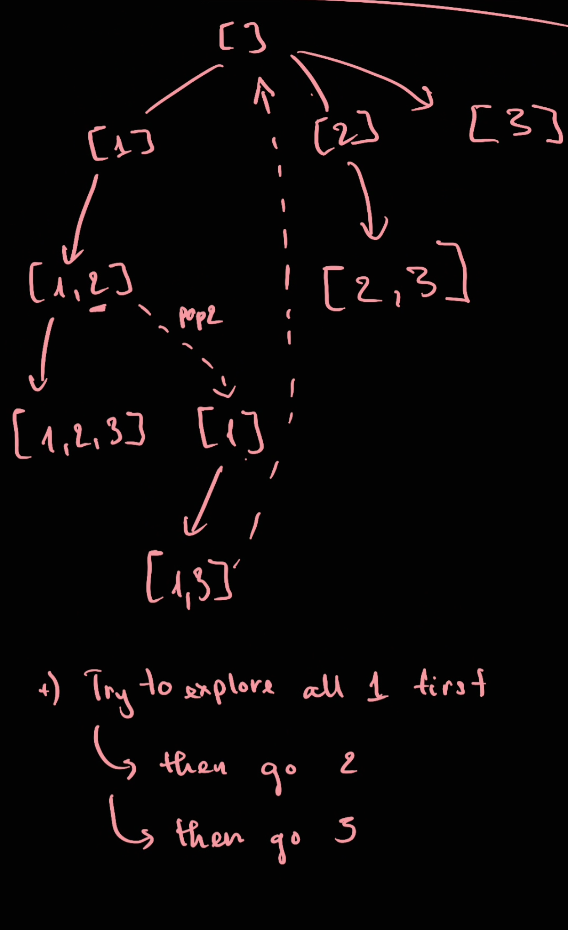
Iteration 0: [[]]
Iteration 1: [[], [1]]
Iteration 2: [[], [1], [1, 2]]
Iteration 3: [[], [1], [1, 2], [1, 2, 3]]

Iteration 4: [[], [1], [1, 2], [1, 2, 3], [1, 3]]
Iteration 5: [[], [1], [1, 2], [1, 2, 3], [1, 3], [2]]
Iteration 6: [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3]]

So this is more like a DFS where you explore all the option for 1 first before explore the option for 2

class App:
    result: List[int]
    
    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.result = []
        self._subsets(nums, 0)
        return self.result

    def _subsets(self, nums: List, index: int, basket = []):
        self.result.append(basket.copy())
        
        for i in range(index, len(nums)):
            basket.append(nums[i])
            self._subsets(nums, i + 1, basket)
            basket.pop()

^473ad2

Note: The reason why we using a for loop here is:

• range(index, len(nums) to avoid re-picking the number that we've already seen. Hence, the next backtrack will only pick forward to the right.
• At each index, we run a for loop to select the next number and start a new recursion cycle
  • If that new cycle doesn't work, we can choose a different candidate
  • When i > index, that means we started popping back and switch candidate already.

However because of tmp.pop() we significantly reduce our space to only using the one that we need (in this case we have 3 elements so size of tmp == 3)

[!note]
At each element, we want to just add the subset that was created by that item. We don't have to worry about the guard check condition here because the for loop will actually stop the recursion from keep going.

Time complexity:

• $O(n \times 2^n)$
  • $n$ numbers will have $2^n$ subsets
  • Each time you do basket.copy() that is $O(n)$

Subset duplication (Recommended way)

https://leetcode.com/problems/subsets-ii/

When the question ask you if a subset can contain duplicate. For example

Input: nums = [1,2,2]
Output: [[],[1],[1,2],[1,2,2],[2],[2,2]]

using the above method, we could possible generate [1,2] twice (because there are 2 different 2)

If we use the same algorithm above, this will happen

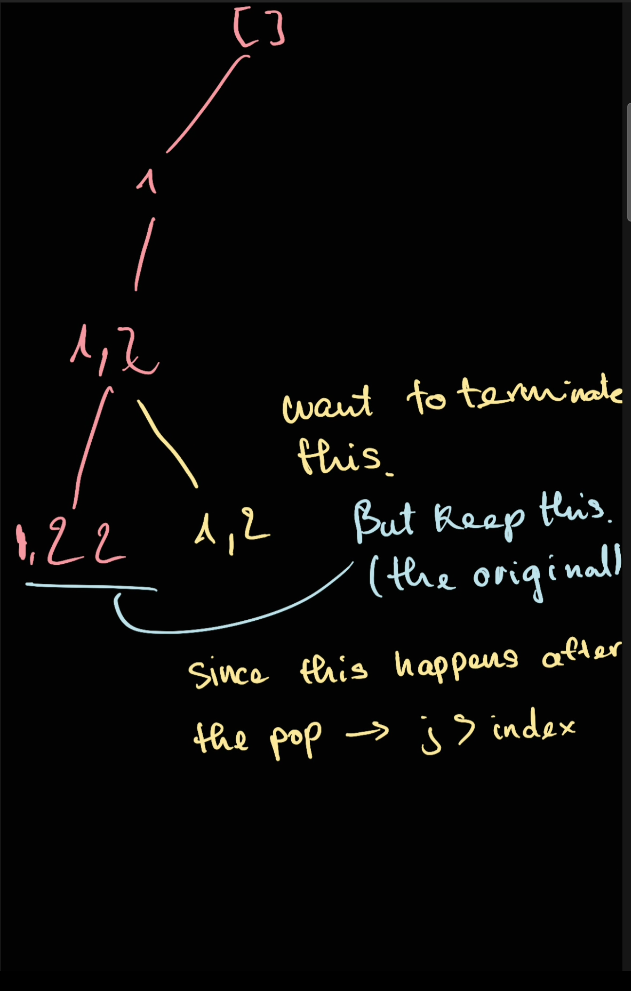
def generateAllSubsetsUsingBacktrackingBuildUpNoDup(nums: List[int]) -> List[int]:
    def backtracking(index: int, tmp=[]):
        nonlocal result

        result.append(tmp.copy())

        for j in range(index, len(nums)):
            if j > index and nums[j] == nums[j - 1]: # If we already visited this number (and it's not the intial buildup)
                continue
            tmp.append(nums[j])
            backtracking(j + 1, tmp)
            tmp.pop()

    result = []
    nums.sort() # First we need to sort
    backtracking(0)
    return result

class App:
    result: List[int]
    
    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.result = []
        self._subsets(nums, 0)
        return self.result

    def _subsets(self, nums: List, index: int, basket = []):
        self.result.append(basket.copy())
        
        for i in range(index, len(nums)):
			if i > index and nums[i] == nums[i - 1]: # If we already visited this number (and it's not the intial buildup)
				continue
            basket.append(nums[i])
            self._subsets(nums, i + 1, basket)
            basket.pop()

The reason why we need to sort because it's impossible to dishtinguish between 2,1,2 and 2,2,1 or 1,2,2. By sorting the number, we are forcing only one possible combination of 1,2,2. Hence the sort. ^d9061d

Next, we need to skip the number we have already selected (duplicated) nums[i] != nums[i - 1] if only when the algorithm pop back i > index. This will guarantee that we don't start from the same number again

Sorting will take $O(nlogn)$. So the algorithms will take $O(nlogn + n\times2^n)$