Merge Intervals

When dealing with the case of overlapping interval, we have 6 different cases.

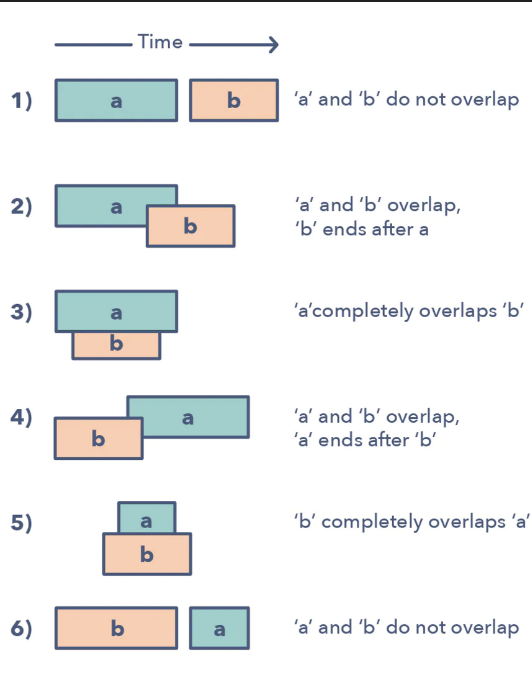
Ways to identify

• When the question as you to produce a list with only mutually excusive
• Overlapping intervals

Formula

isOverlap

Two number is overlap if
$$startA \leq endB \quad \textrm{and} \quad startB \leq endA$$
Proof:

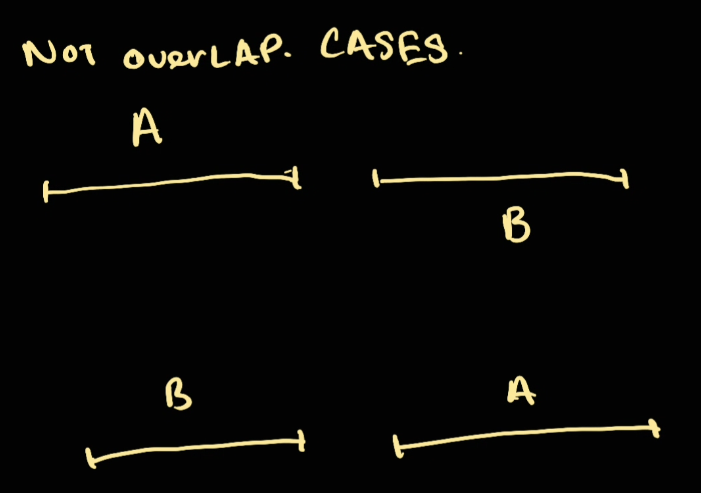
First, we need to consider when the 2 ranges will not overlap. They will not overlap if $endA \lt startB$ or $endB \lt startA$.

So they will overlap if the not overlap case doesn't happen.

Therefore

• $!(endA \lt startB \quad || \quad endB \lt startA)$
• Using De Morgan's Laws we have:
  • $!(endA \lt startB) \quad \textbf{and} \quad !(endB \lt startA)$
• So we have
  • $(endA \geq startB) \quad \text{and} \quad (endB \geq startA)$

Merge

$$mergeInterval = [\min(startA, startB), \max(endA, endB)]$$

• $merge((1,4), (3,5)) = (min(1,3), max(4,5)) = (1,5)$
• $merge((2,9), (3,5)) = (min(2,3), max(9,5)) = (2,9)$

Example

Merge Interval

https://leetcode.com/problems/merge-intervals/solutions/127480/merge-intervals/

Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlap, merge them into [1,6].

This question we need to sort first because in the test cases there is 1 case that put [1,10000] in the end. Without sorting we cannot go back and modify our result array

• Time Complexity: $O(nlogn)$ because of sorting
• Space complexity: $O(n)$ as we need a new array to store our result

Intuition

We keep considering if the previous number can be merged with the current number

class App:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:
        result = []
        if len(intervals) == 0: return result

        # Why sort? Because there is a test case that won't work if we don't sort
        # We want the list to be sorted from small -> large before doing this
        # Else if we're at the end and we have a [1,10000], we can't do it
        intervals = sorted(intervals, key=lambda i: i[0])
        mergeInterval = None
        
        for interval in intervals:
            if not mergeInterval:
                mergeInterval = interval
                continue
            
            if self.mergable(interval, mergeInterval):
                mergeInterval = self._merge(interval, mergeInterval)
            else:
                # We keep appending the mergeInterval because it's always the last
                # element even if we can't do a merge
                result.append(mergeInterval)
                mergeInterval = interval
        
        if mergeInterval is not None:
            result.append(mergeInterval)

        return result

    def mergable(self, intervalA, intervalB):
        """
        proof: https://swe.auspham.dev/docs/algorithms/arrays/merge-intervals/#isoverlap
        """
        startA, endA = intervalA
        startB, endB = intervalB
        return endA >= startB and endB >= startA

    def _merge(self, intervalA, intervalB): 
        startA, endA = intervalA
        startB, endB = intervalB
        return [min(startA, startB), max(endA, endB)]

Insert Interval

https://leetcode.com/problems/insert-interval/

Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]

This question we don't need to sort because the condition give us the intervals array sorted and non-overlapped.

• In real interview, make sure to clarify this limitation carefully to avoid over-thinking
• If the interviewer say this could be overlapped, we then insert the newInterval inside the intervals array and perform a sort. Therefore comes back to the Merge Interval problem

Intuition

For this question, we don't consider merging with the last element. This is because since the array is non-overlapped, merging only happens once from the moment we use newInterval.

Therfore, we only insert the mergeInterval once in the correct position.

class App:
    def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
        if len(newInterval) == 0: raise Exception("Invalid Arguments")
        
        result = []
        mergeInterval = newInterval
        
        for interval in intervals:
            if mergeInterval and self.mergable(interval, mergeInterval):
                mergeInterval = self.merge(interval, mergeInterval)
            else:
                # add mergeInterval in if the current interval > mergeInterval
                if mergeInterval and interval[0] > mergeInterval[1]:
                    result.append(mergeInterval)
                    mergeInterval = None
                result.append(interval)
        
        if mergeInterval is not None:
            result.append(mergeInterval)
            mergeInterval = None

        return result
    
    def merge(self, intervalA, intervalB):
        startA, endA = intervalA
        startB, endB = intervalB
        return [min(startA, startB), max(endA, endB)]
    
    def mergable(self, intervalA, intervalB):
        startA, endA = intervalA
        startB, endB = intervalB
        
        # Proof: https://swe.auspham.dev/docs/algorithms/arrays/merge-intervals/
        return startA <= endB and startB <= endA