Maximum Subarray (Kadane'S Algorithm)

Kadane's algorithm is to calculate the maximum subarray sum ending at the previous postion

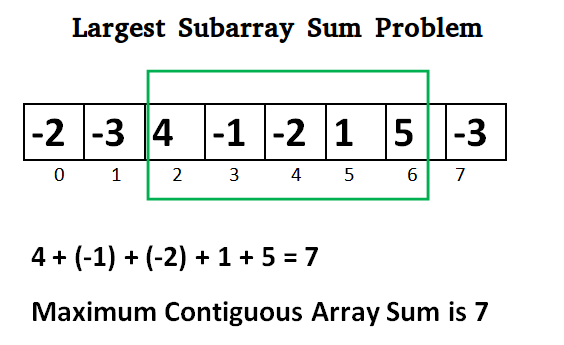
Note: this looks like a Sliding Windows problem but it's not, because the window size is not fixed. We can also do sliding windows way but eventually it's still Kadane's algorithm.

This is a Greedy Algorithm because at one point we always choose the local optimal result.

Example: https://leetcode.com/problems/maximum-subarray/description/

class App:
    def maxSubArray(self, nums: List[int]) -> int:
        if len(nums) == 0: raise Exception("Array can't be empty")
        
        subArrayTotal, maxSubTotal = float('-inf'), float('-inf')
        
        for num in nums:
            subArrayTotal = max(subArrayTotal + num, num)
            maxSubTotal = max(subArrayTotal, maxSubTotal)
        
        return maxSubTotal

The idea is if the sub array is smaller than starting a new sub array again at the current number: we might as well start it at the current number

Because the subArrayTotal restarting multiple time and it's hard to keep track of which one is the best, we use maxSubTotal to keep track of the best subArrayTotal

Similarly, if we want to return the sub array itself, we can do as following based on the same concept

    def maxSubArrayReturnList(self, nums: List[int]) -> List[int]:
        if len(nums) == 0: raise Exception("Array can't be empty")
        
        subArray, maxSub = [], []
        
        for num in nums:
            if sum(subArray) + num >= num:
                subArray.append(num)
            else:
                subArray = [num]

            if sum(subArray) > sum(maxSub):
                maxSub = subArray.copy()
        
        return maxSub