PrefixPostFix Product

Problem statement

Problem: https://leetcode.com/problems/product-of-array-except-self/description/

Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].

The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

You must write an algorithm that runs in O(n) time and without using the division operation.

Example 1:

Input: nums = [1,2,3,4]
Output: [24,12,8,6]

Example 2:

Input: nums = [-1,1,0,-3,3]
Output: [0,0,9,0,0]

Solution

The trick is to calculate the prefix and the postfix of of each number.

• $prefix(x)$: The product of all numbers before $x$ (inclusive)
• $postfix(x)$: The product of all numbers after $x$ (inclusive)

And if we want to have the product without $x$. We have the formula:
$$ \text{product without x} = prefix(x-1) \times postfix(x+1) $$

For example with these number [3,9,5,4] we have the following table:

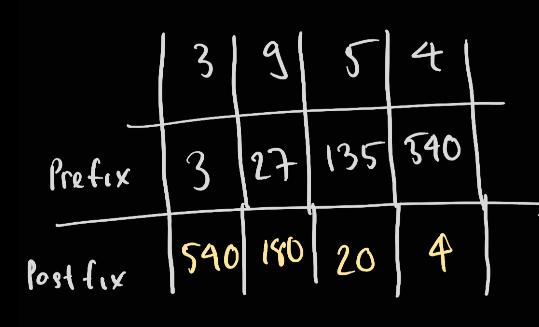
Explaination:

• $prefix(3)$ = $3$

• $prefix(9)$ = $3 \times 9 = 27$

• $prefix(5)$ = $3 \times 9 \times 5 = 135$

• $prefix(4)$ = $3 \times 9 \times 5 \times 4 = 540$

• $postfix(4) = 4$

• $postfix(5) = 4 \times 5 = 20$

• $postfix(9) = 4 \times 5 \times 9 = 180$

• $postfix(3) = 4 \times 5 \times 9 \times 3 = 540$

Therefore, for example to calculate the product of without 9 we can take prefix(3) - product of all numbers before 9 - and times with postfix(5) - product of all numbers after 9.

For those number that's out of the range for postfix and prefix, we intialise it to 1.

As a result, we have the following answer:

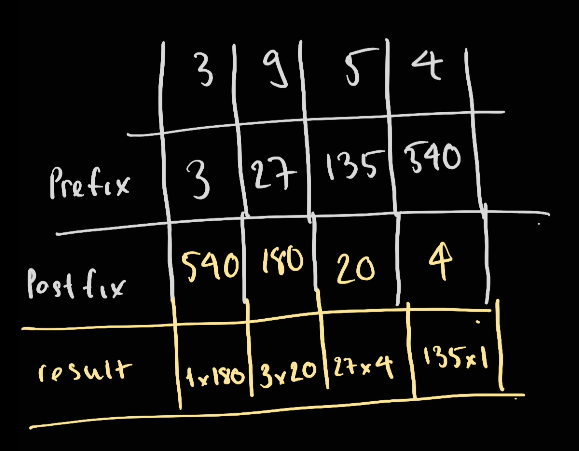
Therefore:

[180, 60, 108, 135]

Implementation

from unittest import TestCase, main
from typing import *
from collections import deque

class App:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        if len(nums) < 2: return nums

        beforeCurrentNumberProduct = []
        lastProduct = 1
        for num in nums:
            lastProduct *= num
            beforeCurrentNumberProduct.append(lastProduct)
        
        afterCurrentNumberProduct = deque()
        lastProduct = 1
        for i in range(len(nums) - 1, -1, -1):
            lastProduct *= nums[i]
            afterCurrentNumberProduct.appendleft(lastProduct)
        
        result = [1] * len(nums)
        for i in range(len(result)):
            result[i] = self.getProduct(i - 1, beforeCurrentNumberProduct) *\
                        self.getProduct(i + 1, afterCurrentNumberProduct)
        return result
    
    def getProduct(self, index: int, productArray: List[int]) -> int: 
        if index < 0 or index >= len(productArray):
            return 1
        return productArray[index]

Time complexity: O(n)
Space complexity: O(n)

Optimisation

As you have notice, we can properly store the result of prefix and postfix into a variable and calculate it on the fly. So that we can reduce our space to O(1).

class App:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        if len(nums) < 2: return nums
        result = [1] * len(nums)

        currentPrefixProduct = 1
        for i, num in enumerate(nums):
            result[i] = currentPrefixProduct
            currentPrefixProduct *= num
        
        currentPostfixProduct = 1
        for i in range(len(nums) - 1, -1, -1):
            num = nums[i]
            result[i] *= currentPostfixProduct
            currentPostfixProduct  *= num
        
        return result

currentPrefixProduct is for accumulating the product before result[i]. Because of that result[i] should store 1 result behind

currentPostfixProduct is for accumulating the product after result[i]. Because of that we need to calculate the currentPostfixProduct first before times it to result[i]

Time Complexity: $O(n)$
Space Complexity: $O(1)$